phitheta2azelpat
Convert radiation pattern from phi-theta coordinates to azimuth-elevation coordinates
Syntax
Description
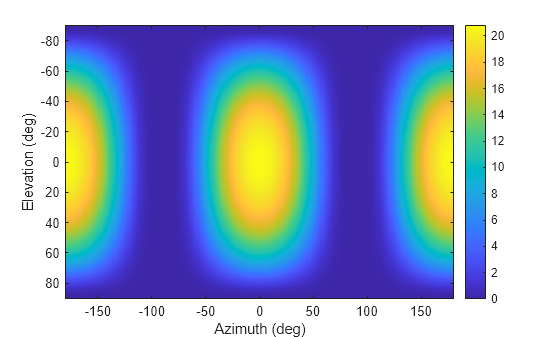
pat_azel = phitheta2azelpat(pat_phitheta,phi,theta)pat_phitheta, from phi
and theta coordinates to the pattern pat_azel in azimuth and
elevation coordinates. phi and theta are
the phi and theta coordinates at which pat_phitheta values are
defined. The pat_azel matrix covers azimuth values from –180 to
180 degrees and elevation values from –90 to 90 degrees in one degree increments.
The function interpolates the pat_phitheta matrix to estimate
the response of the antenna in a given direction.
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2012a