Swash Plate
(To be removed) Swash plate mechanism
The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead. (since R2020a)
For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.
Library
Pumps and Motors
Description
Note that this reference page is for the Hydraulics (Isothermal) Liquid library block. For the Isothermal Liquid library block, see Swash Plate.
The Swash Plate block is a model of a swash plate mechanism used in axial-piston hydraulic pumps and motors to convert translational motion of a piston into rotational motion of a drive shaft. The mechanism is a combination of a cylinder block or rotor, with the piston fitted inside, and an angled swash plate.
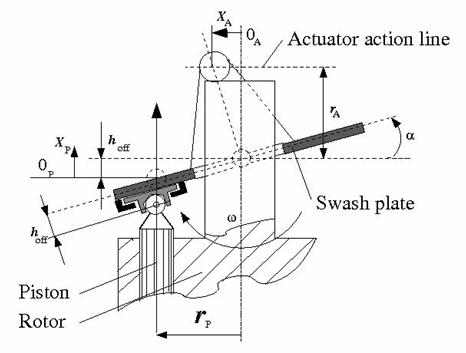
The angular position of the plate is controlled by an actuator, usually a servo cylinder, acting along the actuator action line (marked in the preceding diagram). The distance between the actuator line and the swash plate at zero angle is equal to the actuator arm length rA. The pistons are offset by hoff from the swash plate. The swash plate angle can be changed to increase or decrease the piston stroke. As the rotor turns, the piston slides on the swash plate, which causes the piston to reciprocate. The sliding contact between the piston and the swash plate is maintained by the guideway shown in the diagram.
In a hydraulic machine, the piston moves along the slots in the porting plate (not shown in the preceding diagram) thus being periodically connected to either the intake or the discharge port of the machine. The model simulates a single piston interacting with the swash plate. Mechanically, the mechanism performs summation of two motions, caused by rotation of the swash plate with respect to its axis and rotation of the rotor, and converts them into displacement of the piston.
The following illustration shows the calculation diagram of the mechanism.

The positive direction of the actuator is assumed to be directed to the left from the vertical axis, while the positive direction of the piston motion is directed upward, as it is shown in the diagram. The reference point for both motions corresponds to the plate being perpendicular to the rotor axis. As far as the angular motion of the rotor is concerned, the clockwise rotation (looking from the top) is assumed to be positive.
The piston displacement at arbitrary rotor rotation angle γ and actuator displacement xA is determined from the relationship:
which, after minor rearrangement, yields:
| (1) |
where
| xP | Piston displacement |
| xA | Actuator displacement |
| rP | Cylinder block pitch radius |
| rA | Actuator arm |
| γ | Rotor angle of rotation |
| hoff | Piston offset |
| β | Piston phase angle |
| ω | Rotor angular velocity |
| t | Time |
The kinematic relationship between piston and actuator displacement must be converted into a relationship between the basic Across variables for the physical network representation, that is, velocities:
where
| VP | Piston velocity |
| VA | Actuator velocity |
The inertia properties of the mechanism are assumed to be negligible. Therefore, any state of the mechanism can be considered as equilibrium. According to the principle of virtual work, if the system is in equilibrium the aggregate work of all the applied forces and torques on the system virtual displacements is equal to zero. For the mechanism under consideration, the principle of virtual work yields:
| (2) |
where
| FP | Piston force |
| FA | Actuator force |
| T | Rotor torque |
| Tres | Resistance torque acting on the rotor due to viscous friction |
Virtual displacements δxP, δxA, and δγ are determined from Equation 1 and substituted into Equation 2. Since virtual displacements δxA and δγ are independent, any of them can be equal to zero. As a result, we obtain two more equations of the mechanism:
The resistance torque is:
where μ is the viscous friction coefficient in the contact between the piston and the plate.
The final set of equations describing the swash plate mechanism takes the form:
Connection P is a mechanical translational conserving port associated with the tip of the piston. Connection S is a mechanical rotational conserving port associated with the drive shaft, which is connected to the cylinder block. Connection A is a mechanical translational conserving port associated with the swash plate actuator.
Basic Assumptions and Limitations
The model accounts for the viscous friction in the piston-plate contact.
No inertial effects are considered.
The plate angular displacements are considered to be small.
The joint between the piston and the plate permanently maintains contact between the piston and the plate.
Parameters
- Swash plate actuator arm
The distance between the actuator line of action and the center of the rotor rotation. The parameter must be greater than zero. The default value is
0.065m.- Piston pitch radius
The radius of the pitch circle where the pistons are located, that is, the cylinder block pitch radius. The parameter must be greater than zero. The default value is
0.05m.- Piston offset from the plate
The offset between the piston tip and the swash plate. The parameter must be greater than or equal to zero. The default value is
0.- Phase angle
Parameter sets the piston initial angular position with respect to the reference point which corresponds to the zero angle. The default value is
0.- Actuator initial displacement
Parameter sets the initial position of the actuator with respect to the reference point which corresponds to the plate being perpendicular to the axis of rotor rotation. The default value is
0.- Viscous friction coefficient
The parameter specifies the coefficient of viscous friction in the contact between the piston and the plate. The parameter must be greater than zero. The default value is
50N/(m/s).
Ports
The block has the following ports:
AMechanical translational conserving port associated with the actuator joint.
PMechanical translational conserving port associated with the tip of the piston.
SMechanical rotational conserving port associated with the drive shaft.
Examples
The Hydraulic Axial-Piston Pump with Load-Sensing and Pressure-Limiting Control example models a test rig designed to investigate interaction between an axial-piston pump and a typical control unit, simultaneously performing the load-sensing and pressure-limiting functions. To assure required accuracy, the model of the pump must account for such features as interaction between pistons, swash plate, and porting plate, which makes it necessary to build a detailed pump model.

