Synchronous Machine SI Fundamental
(To be removed) Model dynamics of three-phase round-rotor or salient-pole synchronous machine using fundamental parameters in SI units
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Libraries:
Simscape /
Electrical /
Specialized Power Systems /
Electrical Machines
Description
The Synchronous Machine SI Fundamental block models a synchronous machine in generator or motor mode using fundamental parameters in SI units. The operating mode is dictated by the sign of the mechanical power (positive for generator mode or negative for motor mode). The electrical part of the machine is represented by a sixth-order state-space model and the mechanical part is the same as in the Simplified Synchronous Machine block.
The model takes into account the dynamics of the stator, field, and damper windings. The equivalent circuit of the model is represented in the rotor reference frame (qd frame). Stator windings are connected in wye to an internal neutral point. All rotor parameters and electrical quantities are viewed from the stator and identified by primed variables. The subscripts are:
d,q — d- and q-axis quantity
R,s — Rotor and stator quantity
l,m — Leakage and magnetizing inductance
f,k — Field and damper winding quantity
The electrical model of the machine is shown in these diagrams.

Dynamic Model with Unequal Mutual Inductance
The conventional theory of synchronous machine modeling for stability analysis assumes that the mutual inductances between the armature, damper, and field on direct-axis windings are identical. Generally, damper windings are near the air gap, and as a result the flux linking damper circuits are almost equal to the flux linking armature. This hypothesis produces acceptable outcomes for a wide range of stability studies, especially those on the side of the network. However, when it comes to field current studies, there is considerable error. The equivalent circuit dynamic model of a synchronous machine may include an additional inductance representing the difference between field-damper and field-armature mutual inductances on the D-axis [1]. This inductance is typically called Canay inductance. Canay inductance corresponds to the leakage flux, ΦC, in the following figure and is interpreted as a corrective element in an equivalent model that may have a negative value [2].

The IEEE® standard 1110-2002 [3] presents the direct and quadratic axes of the synchronous machine dynamic model as shown in the diagrams.

The relevant equations are:
Base Values, Transformation Ratio, and Rotor Parameters Referred to the Stator
The Synchronous Machine SI Fundamental block allows you to specify the fundamental parameters of a synchronous machine. You enter field and damper winding parameters (resistances, leakage inductances, and mutual inductances) in SI (Ω, H). The RL parameters of the field and damper windings are not the actual field RL values of the machine but the RL values referred to the stator.
This table displays the stator base values.
| Base stator voltage = peak nominal line-to-neutral voltage (V) |
| Base stator current (A) |
| Base stator impedance (Ω) |
| Base angular frequency (rad/s) |
| Base stator inductance (H) |
where:
Pn is the three-phase nominal power (VA).
Vn is the nominal line-to-line voltage (Vrms).
fn is the nominal frequency (Hz).
ifn is the nominal field current producing nominal stator voltage at no load (A).
The stator parameters to specify in the block are:
| Rs | Stator resistance per phase (Ω) |
| Ll | Stator leakage inductance (H) |
| Lmd | Direct-axis magnetizing inductance viewed from stator (H) |
| Lmq | Quadrature-axis magnetizing inductance viewed from stator (H) |
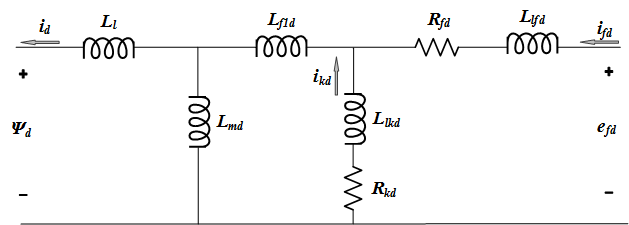
This figure shows one phase of the stator winding coupled with the field winding.

In the diagram:
Ns and Nf are the equivalent number of sinusoidally distributed turns of the stator winding and of the field winding, respectively.
Rs and Ll are stator resistance and leakage inductance.
Rf′ and Llfd′ are field resistance and leakage inductance.
When the three stator windings are energized with a three-phase positive-sequence voltage and the field winding is open, the stator magnetizing inductance is Lmd. However, when only one phase is energized and the field winding is open, the magnetizing inductance is 2/3 Lmd, as shown in the figure.
At no load, when the field winding is rotating at nominal speed and bears the nominal field DC current ifn, the amplitude of AC voltage (peak value) induced on one phase of the stator is Vsbase.
The maximum mutual inductance between one stator winding and the field winding is obtained when the two windings are aligned and is given by:
from which we deduce the transformation ratio:
The transformation ratio can be also expressed as:
where Ifbase is the base field current. The table shows how to compute field base values.
| Base field current (A) |
| Base field voltage (V) |
| Base field impedance (Ω) |
| Base field inductance (H) |
The actual field parameters are:
Rf′ is field resistance (Ω)
Llfd′ is field leakage inductance (H)
You can specify field parameters for the field resistance and leakage inductance referred to the stator (Rf, Llfd).
If the nominal field current ifn is known, the transformation ratio Ns / Nf is calculated using the same equation as for the stator/field transformation ratio.
According to Krause [4], the field voltage and current referred to the stator (Vf, If) are deduced from actual Vf′ , If′ values as follows:
When the actual field resistance Rf′ and leakage inductances Llfd′ (seen from the rotor) are known, the values referred to the stator are:
When the nominal field current is not known, and if the pu values of field resistance and leakage inductances are known (Rf_pu, Llfd_pu), the corresponding SI values referred to the stator are computed as follows:
The same conversions are used for RL parameters of damper windings.
When you specify the nominal field current, the signal at the Vf input port corresponds to the actual field voltage, as in real life. The field current returned by the measurement output also corresponds to the actual field current If.
The nominal field voltage producing nominal stator voltage at no load is given by:
When you do not specify the nominal field current, the signal at the Vf input port corresponds to the actual field voltage referred to the stator. In this case, the nominal field voltage referred to the stator producing nominal stator voltage at no load is:
The field current returned by the measurement output is the field current referred to the stator. The nominal field current referred to the stator is:
Assumptions and Limitations
In discrete systems, when you set the Discrete solver model
parameter of a Synchronous Machine block to Trapezoidal non
iterative, you might have to connect a small parasitic resistive load
at the machine terminals to avoid numerical oscillations. Large sample times require
larger loads. The minimum resistive load is proportional to the sample time. As a rule
of thumb, remember that with a 25 μs time step on a 60 Hz system, the minimum load is
approximately 2.5% of the machine nominal power. For example, a 200 MVA synchronous
machine in a power system discretized with a 50 μs sample time requires approximately 5%
of resistive load or 10 MW. If the sample time is reduced to 20 μs, a resistive load of
4 MW should be sufficient.
However, if you set the Discrete solver model parameter of a
Synchronous Machine block to Trapezoidal iterative (alg.
loop), you can use a negligible parasitic load (below 0.1% of nominal
power) while preserving numerical stability. This iterative model produces an algebraic
loop and results in slower simulation speed.
Ports
Input
Output
Conserving
Parameters
References
[1] Canay, I.M. "Causes of Discrepancies on Calculation of Rotor Quantities and Exact Equivalent Diagrams of the Synchronous Machine." IEEE Transactions on Power Apparatus and Systems. PAS-88, no. 7 (1969): 1114–1120.
[2] Moeini, A., et al. “Synchronous Machine Stability model, an Update to IEEE Std 1110-2002 Data Translation Technique.” IEEE standards panel sessions. 2018.
[3] IEEE Guide for Synchronous Generator Modeling Practices and Applications in Power System Stability Analyses. IEEE Std 1110-2002 (Revision of IEEE Std 1110-1991 [2003]): 1–72.
[4] Krause, P.C. Analysis of Electric Machinery. Section 12.5. New York: McGraw-Hill, 1986.
[5] Kundur, P. Power System Stability and Control. New York, McGraw-Hill, 1994.
Extended Capabilities
Version History
Introduced before R2006a