Extract S-Parameters from Mutual Inductor
This example shows how to build a user-defined element from S-parameters and add it to an rfbudget object for link budget analysis using the Symbolic Math Toolbox™. The user-defined element in this example is a mutual inductor.
Consider a mutual inductor as shown in figure 1 with the inductors and . This examples uses the Symbolic Math Toolbox to extract the analytical S-parameters of the mutual inductor and write them an RF Toolbox™ object. To extract S-parameters from a circuit, see Extract S-Parameters from Circuit.

Figure 1: Mutual Inductor
One way to model a mutual inductor in the RF Toolbox is to draw the mutual inductor as an equivalent of a two-port network of inductors in a T configuration. Such a mutual inductor is shown in figure 2 with the mutual inductance and the coupling coefficient . Mutual inductance is given by the equation relates M and k. Inductors in a T configuration can have negative values when there is a strong coupling between the inductors or if the is greater than or .

Figure 2: T-Circuit Representation of Mutual Inductor
Represent Circuit in Node-Branch Form
As discussed in the Extract S-Parameters from Circuit example, to extract S-parameters from a circuit you need to drive one port while terminating the other. This is shown in figure 3. Use constitutive and conservative equations to represent the circuit in node-branch form. There are eight unknowns, five branch currents and three node voltages. Therefore there are eight equations in the node-form, five constitutive equations for the branches and three conservative equations obtained from the Kirchoff's Current Law for the nodes. The constitutive equation for a resistor is derived from Ohm's Law,, and the constitutive equation for an inductor is given by , where s is a complex frequency.
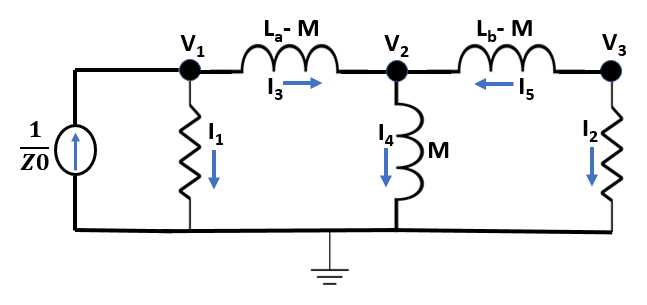
Figure 3: Mutual Inductor Driven at Port 1 with Current Source
syms F syms I [5 1] syms V [3 1] syms Z0 La Lb M s nI=5; % number of branch currents nV=3; % number of node voltages % F = [Fconstitutive; Fconservative] F = [ V1 - Z0*I1 V1 - V2 - (La-M)*I3*s V2 - M*I4*s V2 - V3 + (Lb-M)*I5*s V3 - I2*Z0 I1 + I3 I4 - I5 - I3 I2 + I5 ]
F =
Compute Jacobian
Determine the Jacobian with respect to the unknowns, the five branch currents and three node voltages.
J = jacobian(F,[I; V]);
Solve S-parameters for Further Analysis
As shown in the Extract S-Parameter from a Circuit example, create the right-hand side, rhs vector to the drive and terminate ports.
syms rhs [nI+nV 2] syms x v S t % Compute S-parameters of cascade rhs(:,:) = 0; rhs(nI+1,1) = 1/Z0; % rhs for driving input port rhs(nI+nV,2) = 1/Z0 % rhs for driving output port
rhs =
By backsolving rhs, solve for the voltages using Jacobian.
x = J \ rhs; v = x(nI+[1 nV],:); S = (2*v - eye(2));
Create Object for RF Toolbox
In order to create a sparameters object, the parameters must be determined at a set of frequencies. To do so, define the variables for your mutual inductor. If you would like to test multiple values for your variables and automatically update your sparameters object, use Numeric Sliders in the Control drop-down under the Live Editor tab. Then, use the Symbolic Math Toolbox's matlabFunction to automatically generate a function, mutualInductorS to compute the analytic S-parameters at a set of frequencies. Finally, use the sparameters object to create a S-parameters object.
matlabFunction(S,'file','mutualInductorS.m','Optimize',false); La =0.000001; Lb =
0.000001; Z0 =
50; k =
0.763; M = k*((La*Lb)^(1/2)); freq = linspace(1e9,2e9,10); s = 2i*pi*freq; s_param = zeros(2,2,10); for index = 1:numel(freq) s_param(:,:,index) = mutualInductorS(Lb,Lb,M,Z0,s(index)); end Sobj = sparameters(s_param,freq);
Create Object for RF Budget
Use an rfwrite function to create a Touchstone® file from the sparameters object.
rfwrite(Sobj,'mutualInductor.s2p');Create a nport object.
n = nport('mutualInductor.s2p');Provide the nport object as an input to rfbudget object.
b = rfbudget(n,2.1e9,-30,10e3);
Type this command at the MATLAB Command Window to open the mutual inductor as a S-parameter element in the RF Budget Analyzer app.
show(b)

Using this method you can build your own components for RF budget analysis.