envelope
Signal envelope
Syntax
Description
[ returns
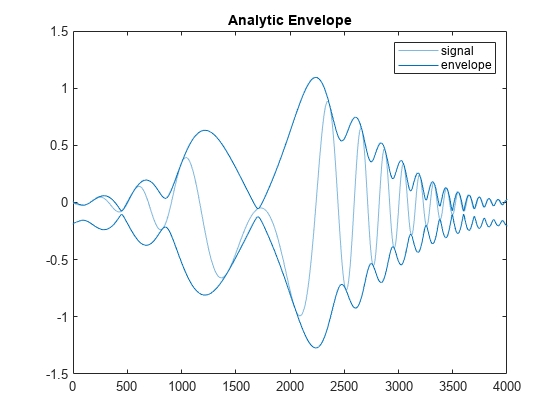
the upper and lower envelopes of the input sequence, yupper,ylower] = envelope(x)x,
as the magnitude of its analytic signal. The analytic signal of x is
found using the discrete Fourier transform as implemented in hilbert. The function initially removes
the mean of x and adds it back after computing
the envelopes. If x is a matrix, then envelope operates
independently over each column of x.
[ returns
the envelopes of yupper,ylower] = envelope(x,fl,'analytic')x determined using the magnitude
of its analytic signal. The analytic signal is computed by filtering x with
a Hilbert FIR filter of length fl. This syntax
is used if you specify only two arguments.
[ returns
the upper and lower root-mean-square envelopes of yupper,ylower] = envelope(x,wl,'rms')x.
The envelopes are determined using a sliding window of length wl samples.
[ returns
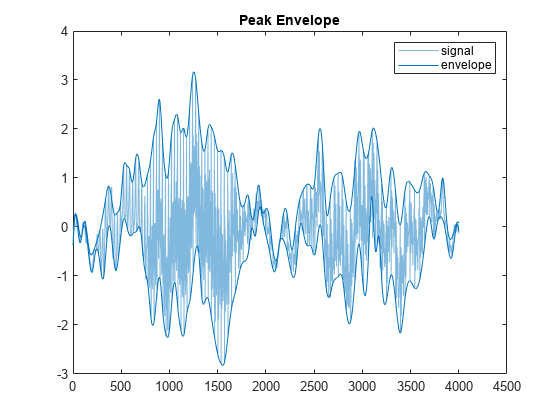
the upper and lower peak envelopes of yupper,ylower] = envelope(x,np,'peak')x. The
envelopes are determined using spline interpolation over local maxima
separated by at least np samples.
envelope(___) with no output
arguments plots the signal and its upper and lower envelopes. This
syntax accepts any of the input arguments from previous syntaxes.