fftfilt
FFT-based FIR filtering using overlap-add method
Description
y = fftfilt(d,x)x with a digitalFilter object d.
Examples
Input Arguments
Output Arguments
More About
Algorithms
fftfilt filters data using the efficient FFT-based method of
overlap-add
[1], a frequency domain
filtering technique that works only for FIR filters by combining successive frequency domain
filtered blocks of an input sequence. The operation performed by fftfilt
is described in the time domain by the difference equation:
An equivalent representation is the Z-transform or frequency domain description:
fftfilt uses fft to implement the overlap-add method. fftfilt breaks an
input sequence x into length L data blocks, where
L must be greater than the filter length N.
![]()
and convolves each block with the filter b by
y = ifft(fft(x(i:i+L-1),nfft).*fft(b,nfft));
where nfft is the FFT length. fftfilt overlaps
successive output sections by n-1 points, where n is the
length of the filter, and sums them.
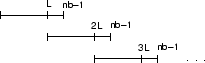
fftfilt chooses the key parameters L and
nfft in different ways, depending on whether you supply an FFT length
n for the filter and signal. If you do not specify a value for
n (which determines FFT length), fftfilt chooses
these key parameters automatically:
If
length(x)is greater thanlength(b),fftfiltchooses values that minimize the number of blocks times the number of flops per FFT.If
length(b)is greater than or equal tolength(x),fftfiltuses a single FFT of length2^nextpow2(length(b) + length(x) - 1)
This computes
y = ifft(fft(B,nfft).*fft(X,nfft))
If you supply a value for n, fftfilt chooses an
FFT length, nfft, of 2^nextpow2(n) and a data block
length of nfft - length(b) + 1. If
n is less than length(b), fftfilt
sets n to length(b).
References
[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.
Extended Capabilities
Version History
Introduced before R2006a
See Also
conv | designfilt | digitalFilter | filter | filtfilt