Main Content

filtfilt

Zero-phase digital filtering

collapse all in page

Syntax

y = filtfilt(b,a,x)
y = filtfilt(sos,g,x)
y = filtfilt(d,x)

Description

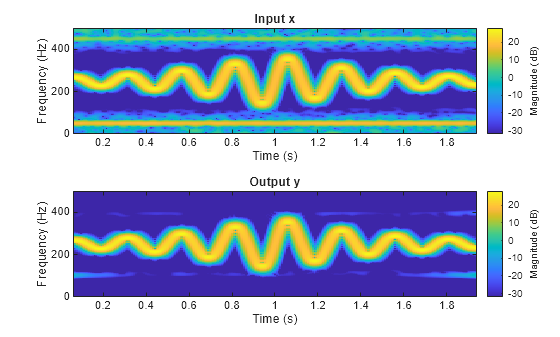
y = filtfilt(b,a,x) performs zero-phase digital filtering by processing the input data x in both the forward and reverse directions. After filtering the data in the forward direction, the function reverses the filtered sequence and runs it back through the filter. The result has these characteristics:

  • Zero phase distortion.

  • A filter transfer function equal to the squared magnitude of the original filter transfer function.

  • A filter order that is double the order of the filter specified by b and a.

filtfilt minimizes start-up and ending transients by matching initial conditions. Do not use filtfilt with differentiator and Hilbert FIR filters, because the operation of these filters depends heavily on their phase response.

y = filtfilt(sos,g,x) zero-phase filters the input data x using the second-order section (biquad) filter represented by the matrix sos and the scale values g.

example

y = filtfilt(d,x) zero-phase filters the input data x using a digital filter d. Use designfilt to generate d based on frequency-response specifications.

Examples

collapse all

Open Live Script

Zero-phase filtering helps preserve features in a filtered time waveform exactly where they occur in the unfiltered signal.

Zero-phase filter a synthetic electrocardiogram (ECG) waveform. The function that generates the waveform is at the end of the example. The QRS complex is an important feature in the ECG. Here it begins around time point 160.

wform = ecg(500);

plot(wform)
axis([0 500 -1.25 1.25])
text(155,-0.4,"Q")
text(180,1.1,"R")
text(205,-1,"S")

Figure contains an axes object. The axes object contains 4 objects of type line, text.

Corrupt the ECG with additive noise. Reset the random number generator for reproducible results. Construct a lowpass FIR equiripple filter and filter the noisy waveform using both zero-phase and conventional filtering.

rng default

x = wform' + 0.25*randn(500,1);
d = designfilt("lowpassfir", ...
    PassbandFrequency=0.15,StopbandFrequency=0.2, ...
    PassbandRipple=1,StopbandAttenuation=60, ...
    DesignMethod="equiripple");
y = filtfilt(d,x);
y1 = filter(d,x);

subplot(2,1,1)
plot([y y1])
title("Filtered Waveforms")
legend("Zero-phase Filtering","Conventional Filtering")

subplot(2,1,2)
plot(wform)
title("Original Waveform")

Figure contains 2 axes objects. Axes object 1 with title Filtered Waveforms contains 2 objects of type line. These objects represent Zero-phase Filtering, Conventional Filtering. Axes object 2 with title Original Waveform contains an object of type line.

Zero-phase filtering reduces noise in the signal and preserves the QRS complex at the same time it occurs in the original. Conventional filtering reduces noise in the signal, but delays the QRS complex.

Repeat the filtering using a Butterworth second-order section filter.

d1 = designfilt("lowpassiir",FilterOrder=12, ...
    HalfPowerFrequency=0.15,DesignMethod="butter");
y = filtfilt(d1,x);

subplot(1,1,1)
plot(x)
hold on
plot(y,LineWidth=3)
legend("Noisy ECG","Zero-Phase Filtering")

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Noisy ECG, Zero-Phase Filtering.

This function generates the ECG waveform.

function x = ecg(L)
%ECG Electrocardiogram (ECG) signal generator.
%   ECG(L) generates a piecewise linear ECG signal of length L.
%
%   EXAMPLE:
%   x = ecg(500).';
%   y = sgolayfilt(x,0,3); % Typical values are: d=0 and F=3,5,9, etc. 
%   y5 = sgolayfilt(x,0,5); 
%   y15 = sgolayfilt(x,0,15); 
%   plot(1:length(x),[x y y5 y15]);

%   Copyright 1988-2002 The MathWorks, Inc.

a0 = [0,1,40,1,0,-34,118,-99,0,2,21,2,0,0,0]; % Template
d0 = [0,27,59,91,131,141,163,185,195,275,307,339,357,390,440];
a = a0/max(a0);
d = round(d0*L/d0(15)); % Scale them to fit in length L
d(15)=L;

for i=1:14
       m = d(i):d(i+1)-1;
       slope = (a(i+1)-a(i))/(d(i+1)-d(i));
       x(m+1) = a(i)+slope*(m-d(i));
end

end

Input Arguments

collapse all

Transfer function coefficients, specified as vectors. If you use an all-pole filter, enter 1 for b. If you use an all-zero (FIR) filter, enter 1 for a.

Example: b = [1 3 3 1]/6 and a = [3 0 1 0]/3 specify a third-order Butterworth filter with a normalized 3-dB frequency of 0.5π rad/sample.

Data Types: single | double

Input signal, specified as a real-valued or complex-valued vector, matrix, or N-D array. x must be finite-valued. The length of x must be greater than three times the filter order, defined as max(length(B)-1, length(A)-1). The function operates along the first array dimension of x unless x is a row vector. If x is a row vector, then the function operates along the second dimension.

Example: cos(pi/4*(0:159))+randn(1,160) is a single-channel row-vector signal.

Example: cos(pi./[4;2]*(0:159))'+randn(160,2) is a two-channel signal.

Data Types: single | double
Complex Number Support: Yes

Second-order section coefficients, specified as a matrix. sos is a K-by-6 matrix where the number of sections K must be greater than or equal to 2. If the number of sections is less than 2, then the function treats the input as a numerator vector. Each row of sos corresponds to the coefficients of a second-order (biquad) filter. The ith row of sos corresponds to [bi(1) bi(2) bi(3) ai(1) ai(2) ai(3)].

Example: s = [2 4 2 6 0 2;3 3 0 6 0 0] specifies a third-order Butterworth filter with a normalized 3-dB frequency of 0.5π rad/sample.

Data Types: single | double

Scale factors, specified as a vector.

Data Types: single | double

Digital filter, specified as a digitalFilter object. Use designfilt to generate a digital filter based on frequency-response specifications.

Example: d = designfilt("lowpassiir",FilterOrder=3,HalfPowerFrequency=0.5) specifies a third-order Butterworth filter with a normalized 3-dB frequency of 0.5π rad/sample.

Output Arguments

collapse all

Filtered signal, returned as a vector, matrix, or N-D array.

If the input to filtfilt is single precision, the function returns output y in single precision.

References

[1] Gustafsson, F. “Determining the initial states in forward-backward filtering.” IEEE® Transactions on Signal Processing. Vol. 44, April 1996, pp. 988–992.

[2] Mitra, Sanjit K. Digital Signal Processing. 2nd Ed. New York: McGraw-Hill, 2001.

[3] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.

Extended Capabilities

Version History

Introduced before R2006a

See Also

| | | |

Topics