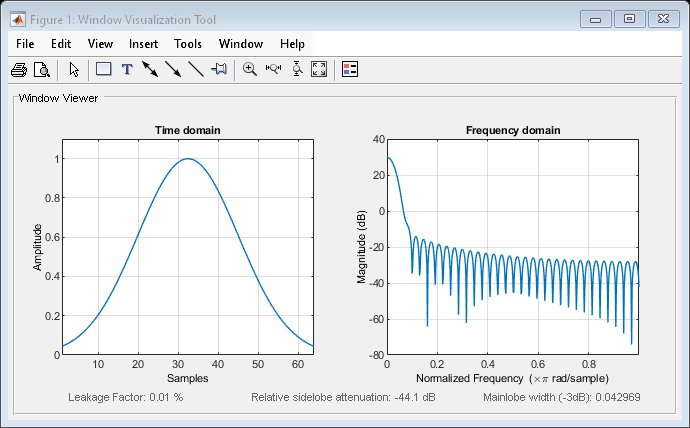
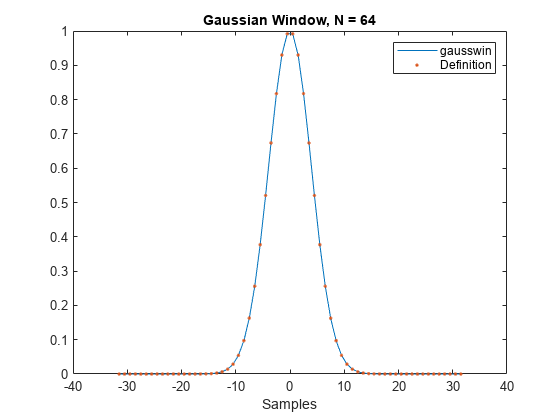
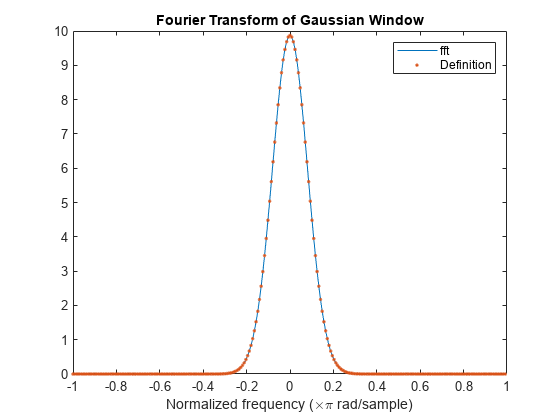
gausswin
Gaussian window
Description
Examples
Input Arguments
Output Arguments
Algorithms
The coefficients of a Gaussian window are computed from the following equation:
where –(L – 1)/2 ≤ n ≤ (L – 1)/2, and α is inversely proportional to the standard deviation, σ, of a Gaussian random variable. The exact correspondence with the standard deviation of a Gaussian probability density function is σ = (L – 1)/(2α).
References
[1] Hansen, Eric W. Fourier Transforms: Principles and Applications. New York: John Wiley & Sons, 2014.
[2] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999.
Extended Capabilities
Version History
Introduced before R2006a