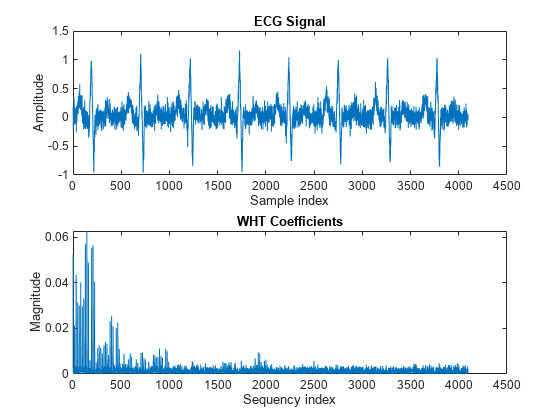
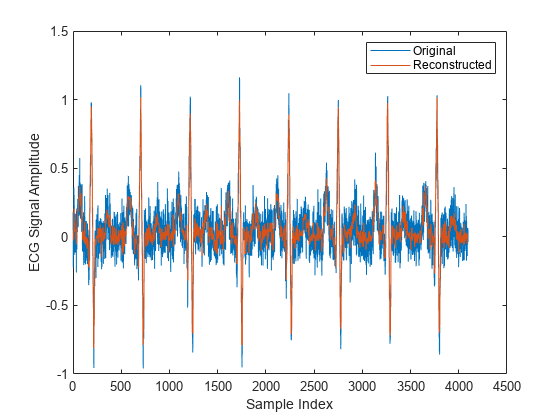
ifwht
Inverse Fast Walsh-Hadamard transform
Description
y = ifwht(x)x.
Examples
Input Arguments
Algorithms
The inverse fast Walsh-Hadamard transform algorithm is similar to the Cooley-Tukey algorithm used for the inverse FFT. Both use a butterfly structure to determine the transform coefficients. For more details, see the references.
References
[1] Beauchamp, Kenneth G. Applications of Walsh and Related Functions: With an Introduction to Sequency Theory. London: Academic Press, 1984.
[2] Beer, Tom. “Walsh Transforms.” American Journal of Physics. Vol. 49, 1981, pp. 466–472.
Extended Capabilities
Version History
Introduced in R2008b