sgolayfilt
Savitzky-Golay filtering
Description
Examples
Input Arguments
Output Arguments
Tips
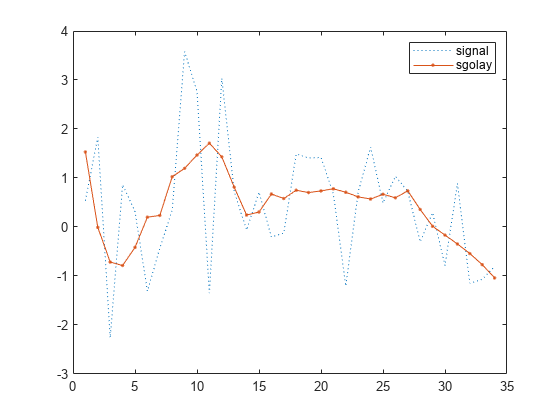
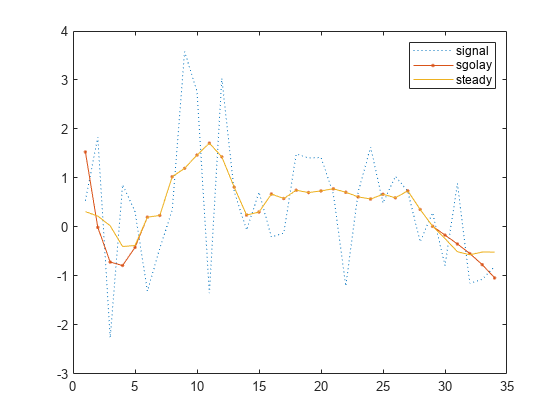
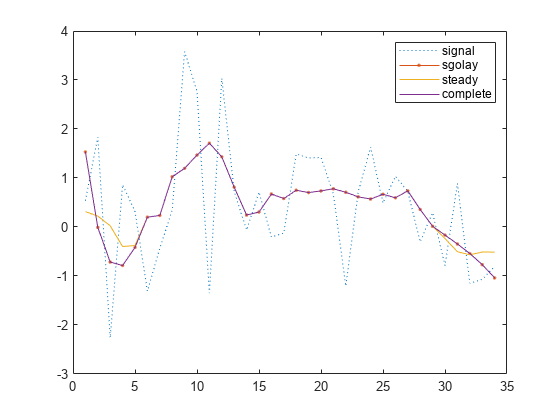
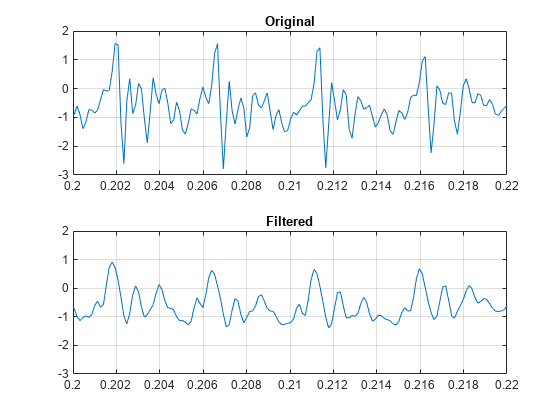
Savitzky-Golay smoothing filters are typically used to "smooth out" a noisy signal whose frequency span (without noise) is large. They are also called digital smoothing polynomial filters or least-squares smoothing filters. Savitzky-Golay filters perform better in some applications than standard averaging FIR filters, which tend to filter high-frequency content along with the noise. Savitzky-Golay filters are more effective at preserving high frequency signal components but less successful at rejecting noise.
Savitzky-Golay filters are optimal in the sense that they minimize the least-squares
error in fitting a polynomial to frames of noisy data. See sgolay for more information about the Savitzky-Golay algorithm.
References
[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1996.
[2] Schafer, Ronald. “What Is a Savitzky-Golay Filter? [Lecture Notes].” IEEE Signal Processing Magazine 28, no. 4 (July 2011): 111–17. https://doi.org/10.1109/MSP.2011.941097.
Extended Capabilities
Version History
Introduced before R2006a