zplane

Zero-pole plot for discrete-time systems

Syntax

zplane(z,p)

zplane(b,a)

zplane(B,A,"ctf")

[hz,hp,ht] = zplane(___)

zplane(d)

[vz,vp,vk] = zplane(d)

Description

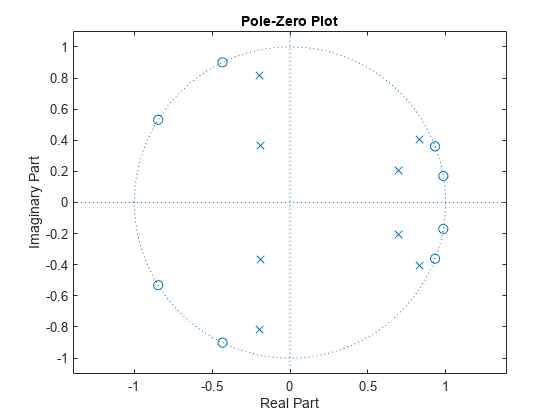
zplane(z,p) plots the zeros and poles of discrete-time systems in the current figure window. Specify the zeros in a column vector z and the poles in a column vector p. The symbol 'o' represents a zero and the symbol 'x' represents a pole. The plot includes the unit circle for reference.

If z and p are matrices, then zplane treats each column as a separate set of poles and zeros, and plots each set in a different color.

zplane(b,a) first uses roots to find the zeros and poles of the transfer function represented by the numerator coefficients b and the denominator coefficients a, and then zplane plots the zeros and poles in the current figure window. Specify b and a as row vectors.

zplane(B,A,"ctf") finds and plots the zeros and poles of the digital filter represented as Cascaded Transfer Functions (CTF) with numerator coefficients B and denominator coefficients A. (since R2024b)

Note

Specify the "ctf" option to disambiguate CTF numerator and denominator matrices B,A from multiple sets of poles and zeros z,p.

[hz,hp,ht] = zplane(___) returns vectors of handles to the zero lines hz and the pole lines hp. ht is a vector of handles to the axes/unit circle line and to text objects, which are present when there are multiple zeros or poles.

zplane(d) finds the zeros and poles of the transfer function represented by the digital filter d. Use designfilt to generate d based on frequency-response specifications.

[vz,vp,vk] = zplane(d) returns the zeros vz, poles vp, and gain vk corresponding to the digital filter d.

Examples

Poles and Zeros of Elliptic Lowpass Filter

For data sampled at 1000 Hz, plot the poles and zeros of a 4th-order elliptic lowpass digital filter with cutoff frequency 200 Hz, 3 dB of ripple in the passband, and 30 dB of attenuation in the stopband.

[z,p,k] = ellip(4,3,30,200/500);
zplane(z,p)
grid
title('4th-Order Elliptic Lowpass Digital Filter')

Create the same filter using designfilt. Use zplane to plot the poles and zeros.

d = designfilt('lowpassiir','FilterOrder',4,'PassbandFrequency',200, ...
               'PassbandRipple',3,'StopbandAttenuation',30, ...
               'DesignMethod','ellip','SampleRate',1000);
zplane(d)

Zeros and Poles of Transfer Function

Design an 8th-order Chebyshev Type II bandpass filter with a stopband attenuation of 20 dB. Specify the stopband edge frequencies as $$\pi /8$$ rad/sample and $$5\pi /8$$ rad/sample.

[b,a] = cheby2(8/2,20,[1 5]/8);

Use zplane to plot the poles and zeros of the transfer function.

zplane(b,a)

Visualize the zero-phase response of the filter. Overlay the unit circle and the pole and zero locations.

[hw,fw] = zerophase(b,a,1024,"whole");

z = roots(b);
p = roots(a);

plot3(cos(fw),sin(fw),hw)
hold on
plot3(cos(fw),sin(fw),zeros(size(fw)),'--')
plot3(real(z),imag(z),zeros(size(z)),'o')
plot3(real(p),imag(p),zeros(size(p)),'x')
hold off
xlabel("Real")
ylabel("Imaginary")
view(35,40)
grid

Zero-Pole Plot from Cascaded Transfer Functions

Since R2024b

Design a 40th-order lowpass Chebyshev type II digital filter with a stopband edge frequency of 0.4 and stopband attenuation of 50 dB. Plot the zeros and poles of the filter in the z-plane using the filter coefficients in the CTF format.

[B,A] = cheby2(40,50,0.4,"ctf");

zplane(B,A,"ctf")

Input Arguments

z, p — Zeros and poles

column vectors | matrices

Zeros and poles, specified as column vectors or matrices. If z and p are matrices, then zplane plots the poles and zeros in the columns of z and p in different colors.

Data Types: single | double
Complex Number Support: Yes

b, a — Transfer function coefficients

row vectors

Transfer function coefficients, specified as row vectors. The transfer function is defined in terms of z^–1:

$$H(z)=\frac{B(z)}{A(z)}=\frac{b(1)+b(2)z^{-1}+\cdots +b(n+1)z^{-n}}{a(1)+a(2)z^{-1}+\cdots +a(m+1)z^{-m}}$$

Example: b = [1 3 3 1]/6 and a = [3 0 1 0]/3 specify a third-order Butterworth filter with normalized 3 dB frequency 0.5π rad/sample.

Data Types: single | double
Complex Number Support: Yes

B,A — Cascaded transfer function (CTF) coefficients

scalars | vectors | matrices

Cascaded transfer function (CTF) coefficients, specified as scalars, vectors, or matrices. B and A list the numerator and denominator coefficients of the cascaded transfer function, respectively.

B must be of size L-by-(m + 1) and A must be of size L-by-(n + 1), where:

• L represents the number of filter sections.

• m represents the order of the filter numerators.

• n represents the order of the filter denominators.

For more information about the cascaded transfer function format and coefficient matrices, see Specify Digital Filters in CTF Format.

Note

If any element of A(:,1) is not equal to 1, then zplane normalizes the filter coefficients by A(:,1). In this case, A(:,1) must be nonzero.

Example: B = [2 4 2;3 3 0] and A = [6 0 2;6 0 0] specify a third-order Butterworth filter with normalized 3 dB frequency 0.5π rad/sample.

Data Types: double | single
Complex Number Support: Yes

d — Digital filter

digitalFilter object

Digital filter, specified as a digitalFilter object. Use designfilt to generate a digital filter based on frequency-response specifications.

Example: d = designfilt("lowpassiir",FilterOrder=3,HalfPowerFrequency=0.5) specifies a third-order Butterworth filter with normalized 3 dB frequency 0.5π rad/sample.

Output Arguments

hz, hp, ht — Vectors of handles

vectors

Vectors of handles to the zero lines, hz, and the pole lines, hp, of the pole-zero plot. ht is a vector of handles to the axes/unit circle line and to text objects, which are present when there are multiple zeros or poles. If there are no zeros or no poles, hz or hp is the empty matrix, [].

vz, vp, vk — Zeros, poles, and gain

column vectors and scalar

Zeros, poles, and gain of a digital filter, d, returned as column vectors and a scalar.

More About

Cascaded Transfer Functions

Partitioning an IIR digital filter into cascaded sections improves its numerical stability and reduces its susceptibility to coefficient quantization errors. The cascaded form of a transfer function H(z) in terms of the L transfer functions H₁(z), H₂(z), …, H_L(z) is

$$H(z)={\displaystyle \prod _{l=1}^L{H}_l(z)}=H_1(z)\times H_2(z)\times \cdots \times H_L(z).$$

Specify Digital Filters in CTF Format

You can specify digital filters in the CTF format for analysis, visualization, and signal filtering. Specify a filter by listing its coefficients B and A. You can also include the filter scaling gain across sections by specifying a scalar or vector g.

Filter Coefficients

When you specify the coefficients as L-row matrices,

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1,m+1}\\ b_{21}& b_{22}& \cdots & b_{2,m+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{L1}& b_{L2}& \cdots & b_{L,m+1}\end{array}\right],A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1,n+1}\\ a_{21}& a_{22}& \cdots & a_{2,n+1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{L,n+1}\end{array}\right],$$

it is assumed that you have specified the filter as a sequence of L cascaded transfer functions, such that the full transfer function of the filter is

$$H\left(z\right)=\frac{b_{11}+b_{12}{z}^{-1}+\cdots +b_{1,m+1}{z}^{-m}}{a_{11}+a_{12}{z}^{-1}+\cdots +a_{1,n+1}{z}^{-n}}\times \frac{b_{21}+b_{22}{z}^{-1}+\cdots +b_{2,m+1}{z}^{-m}}{a_{21}+a_{22}{z}^{-1}+\cdots +a_{2,n+1}{z}^{-n}}\times \cdots \times \frac{b_{L1}+b_{L2}{z}^{-1}+\cdots +b_{L,m+1}{z}^{-m}}{a_{L1}+a_{L2}{z}^{-1}+\cdots +a_{L,n+1}{z}^{-n}},$$

where m ≥ 0 is the numerator order of the filter and n ≥ 0 is the denominator order.

• If you specify both B and A as vectors, it is assumed that the underlying system is a one-section IIR filter (L = 1), with B representing the numerator of the transfer function and A representing its denominator.

• If B is scalar, it is assumed that the filter is a cascade of all-pole IIR filters with each section having an overall system gain equal to B.

• If A is scalar, it is assumed that the filter is a cascade of FIR filters with each section having an overall system gain equal to 1/A.

Note

• To convert second-order section matrices to cascaded transfer functions, use the sos2ctf function.

• To convert a zero-pole-gain filter representation to cascaded transfer functions, use the zp2ctf function.

Coefficients and Gain

If you have an overall scaling gain or multiple scaling gains factored out from the coefficient values, you can specify the coefficients and gain as a cell array of the form {B,A,g}. Scaling filter sections is especially important when you work with fixed-point arithmetic to ensure that the output of each filter section has similar amplitude levels, which helps avoid inaccuracies in the filter response due to limited numeric precision.

The gain can be a scalar overall gain or a vector of section gains.

• If the gain is scalar, the value applies uniformly to all the cascade filter sections.

• If the gain is a vector, it must have one more element than the number of filter sections L in the cascade. Each of the first L scale values applies to the corresponding filter section, and the last value applies uniformly to all the cascade filter sections.

If you specify the coefficient matrices and gain vector as

$$B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1,m+1}\\ b_{21}& b_{22}& \cdots & b_{2,m+1}\\ ⋮& ⋮& \ddots & ⋮\\ b_{L1}& b_{L2}& \cdots & b_{L,m+1}\end{array}\right],A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1,n+1}\\ a_{21}& a_{22}& \cdots & a_{2,n+1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{L,n+1}\end{array}\right],g=\left[\begin{array}{ccccc}{g}_1& g_2& \cdots & g_L& g_{\text{S}}\end{array}\right],$$

it is assumed that the transfer function of the filter system is

$$H\left(z\right)=g_{\text{S}}\left(g_1\frac{b_{11}+b_{12}{z}^{-1}+\cdots +b_{1,m+1}{z}^{-m}}{a_{11}+a_{12}{z}^{-1}+\cdots +a_{1,n+1}{z}^{-n}}\times g_2\frac{b_{21}+b_{22}{z}^{-1}+\cdots +b_{2,m+1}{z}^{-m}}{a_{21}+a_{22}{z}^{-1}+\cdots +a_{2,n+1}{z}^{-n}}\times \cdots \times g_L\frac{b_{L1}+b_{L2}{z}^{-1}+\cdots +b_{L,m+1}{z}^{-m}}{a_{L1}+a_{L2}{z}^{-1}+\cdots +a_{L,n+1}{z}^{-n}}\right).$$

Tips

• You can override the automatic scaling of zplane using

  axis([xmin xmax ymin ymax])

  after calling zplane. This scaling is useful when one or more zeros or poles have such a large magnitude that the others are grouped tightly around the origin and are hard to distinguish.

References

[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.

Version History

Introduced before R2006a

R2025a: Visualize cascaded transfer functions using Create Plot Live Editor task

You can use cascaded transfer functions (CTF) in the Create Plot Live Editor task to visualize the output of zplane interactively.

R2024b: Analyze filters using cascaded transfer functions

The zplane function supports inputs in the cascaded transfer function (CTF) format.

R2023a: Visualize function outputs using Create Plot Live Editor task

You can now use the Create Plot Live Editor task to visualize the output of zplane interactively. You can select different chart types and set optional parameters. The task also automatically generates code that becomes part of your live script.