Slew Rate of Triangular Waveform
This example shows how to use the slew rate as an estimate of the rising and falling slopes of a triangular waveform. Create three triangular waveforms. One waveform has rising-falling slopes of , one waveform has rising-falling slopes of , and one waveform has a rising slope of and a falling slope of . Use slewrate to find the slopes of the waveforms.
Use tripuls to create a triangular waveform with rising-falling slopes of . Set the sampling interval to 0.01 seconds, which corresponds to a sample rate of 100 hertz.
dt = 0.01; t = -2:dt:2; x = tripuls(t);
Compute and plot the slew rate for the triangular waveform. Input the sample rate (100 Hz) to obtain the correct positive and negative slope values.
slewrate(x,1/dt)
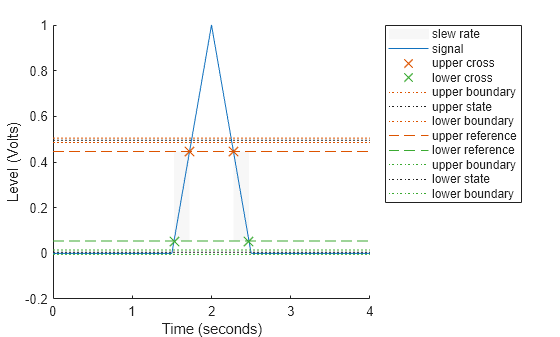
ans = 1×2
2.0000 -2.0000
Change the width of the triangular waveform so it has slopes of . Compute and plot the slew rate.
x = tripuls(t,4); slewrate(x,1/dt)

ans = 1×2
0.5000 -0.5000
Create a triangular waveform with a rising slope of and a falling slope of . Compute the slew rate.
x = tripuls(t,5/2,-3/5); s = slewrate(x,1/dt)
s = 1×2
2.0000 -0.5000
The first element of s is the rising slope and the second element is the falling slope. Plot the result.
slewrate(x,1/dt);
