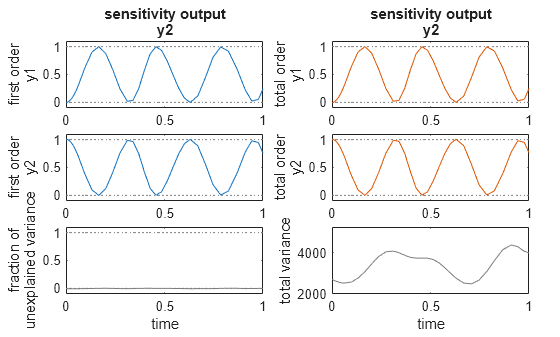
resample
Resample Sobol indices or elementary effects to new time vector
Description
results = resample(gsaObj,timeVector)interp1q interpolation method.
results = resample(gsaObj,timeVector,method)method.
Examples
Input Arguments
Output Arguments
Version History
Introduced in R2020a