sbiosobol
Perform global sensitivity analysis by computing first- and total-order Sobol indices (requires Statistics and Machine Learning Toolbox)
Syntax
Description
sobolResults = sbiosobol(modelObj,params,observables)modelObj by decomposing the variances of
observables with respect to the sensitivity inputs
params.
sobolResults = sbiosobol(modelObj,scenarios,observables)scenarios, a SimBiology.Scenarios
object, to perform the analysis.
sobolResults = sbiosobol(modelObj,params,observables,Name,Value)
Examples
Load the tumor growth model.
sbioloadproject tumor_growth_vpop_sa.sbprojGet a variant with the estimated parameters and the dose to apply to the model.
v = getvariant(m1);
d = getdose(m1,'interval_dose');Get the active configset and set the tumor weight as the response.
cs = getconfigset(m1);
cs.RuntimeOptions.StatesToLog = 'tumor_weight';Simulate the model and plot the tumor growth profile.
sbioplot(sbiosimulate(m1,cs,v,d));
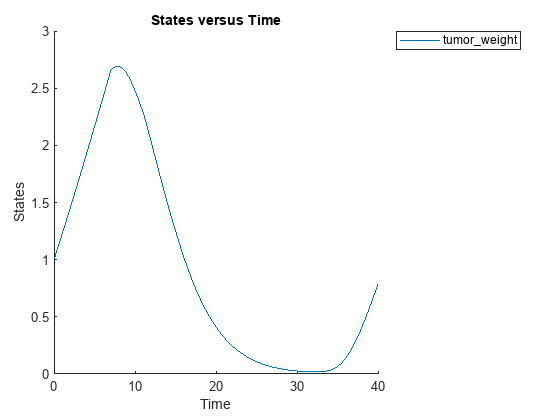
Perform global sensitivity analysis (GSA) on the model to find the model parameters that the tumor growth is sensitive to.
First, retrieve model parameters of interest that are involved in the pharmacodynamics of the tumor growth. Define the model response as the tumor weight.
modelParamNames = {'L0','L1','w0','k1','k2'};
outputName = 'tumor_weight';Then perform GSA by computing the first- and total-order Sobol indices using sbiosobol. Set 'ShowWaitBar' to true to show the simulation progress. By default, the function uses 1000 parameter samples to compute the Sobol indices [1].
rng('default');
sobolResults = sbiosobol(m1,modelParamNames,outputName,Variants=v,Doses=d,ShowWaitBar=true)sobolResults =
Sobol with properties:
Time: [444×1 double]
SobolIndices: [5×1 struct]
Variance: [444×1 table]
ParameterSamples: [1000×5 table]
Observables: {'[Tumor Growth].tumor_weight'}
SimulationInfo: [1×1 struct]
You can change the number of samples by specifying the 'NumberSamples' name-value pair argument. The function requires a total of (number of input parameters + 2) * NumberSamples model simulations.
Show the mean model response, the simulation results, and a shaded region covering 90% of the simulation results.
plotData(sobolResults,ShowMedian=true,ShowMean=false);
![Figure contains an axes object. The axes object with xlabel time, ylabel [Tumor Growth].tumor indexOf w baseline eight contains 12 objects of type line, patch. These objects represent model simulation, 90.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_02.png)
You can adjust the quantile region to a different percentage by specifying 'Alphas' for the lower and upper quantiles of all model responses. For instance, an alpha value of 0.1 plots a shaded region between the 100 * alpha and 100 * (1 - alpha) quantiles of all simulated model responses.
plotData(sobolResults,Alphas=0.1,ShowMedian=true,ShowMean=false);
![Figure contains an axes object. The axes object with xlabel time, ylabel [Tumor Growth].tumor indexOf w baseline eight contains 12 objects of type line, patch. These objects represent model simulation, 80.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_03.png)
Plot the time course of the first- and total-order Sobol indices.
h = plot(sobolResults);
% Resize the figure.
h.Position(:) = [100 100 1280 800];![Figure contains 12 axes objects. Axes object 1 with xlabel time, ylabel total variance contains an object of type line. Axes object 2 with xlabel time, ylabel fraction of unexplained variance contains 3 objects of type line. Axes object 3 with ylabel total order k2 contains 3 objects of type line. Axes object 4 with ylabel first order k2 contains 3 objects of type line. Axes object 5 with ylabel total order k1 contains 3 objects of type line. Axes object 6 with ylabel first order k1 contains 3 objects of type line. Axes object 7 with ylabel total order w0 contains 3 objects of type line. Axes object 8 with ylabel first order w0 contains 3 objects of type line. Axes object 9 with ylabel total order L1 contains 3 objects of type line. Axes object 10 with ylabel first order L1 contains 3 objects of type line. Axes object 11 with title sensitivity output [Tumor Growth].tumor_weight, ylabel total order L0 contains 3 objects of type line. Axes object 12 with title sensitivity output [Tumor Growth].tumor_weight, ylabel first order L0 contains 3 objects of type line.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_04.png)
The first-order Sobol index of an input parameter gives the fraction of the overall response variance that can be attributed to variations in the input parameter alone. The total-order index gives the fraction of the overall response variance that can be attributed to any joint parameter variations that include variations of the input parameter.
From the Sobol indices plots, parameters L1 and w0 seem to be the most sensitive parameters to the tumor weight before the dose was applied at t = 7. But after the dose is applied, k1 and k2 become more sensitive parameters and contribute most to the after-dosing stage of the tumor weight. The total variance plot also shows a larger variance for the after-dose stage at t > 35 than for the before-dose stage of the tumor growth, indicating that k1 and k2 might be more important parameters to investigate further. The fraction of unexplained variance shows some variance at around t = 33, but the total variance plot shows little variance at t = 33, meaning the unexplained variance could be insignificant. The fraction of unexplained variance is calculated as 1 - (sum of all the first-order Sobol indices), and the total variance is calculated using var(response), where response is the model response at every time point.
You can also display the magnitudes of the sensitivities in a bar plot. Darker colors mean that those values occur more often over the whole time course.
bar(sobolResults);
![Figure contains an axes object. The axes object with title sensitivity output [Tumor Growth].tumor_weight, xlabel Sobol Index, ylabel sensitivity input contains 22 objects of type patch, line. These objects represent first order, total order.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_05.png)
You can specify more samples to increase the accuracy of the Sobol indices, but the simulation can take longer to finish. Use addsamples to add more samples. For example, if you specify 1500 samples, the function performs 1500 * (2 + number of input parameters) simulations.
gsaMoreSamples = addsamples(gsaResults,1500)
The SimulationInfo property of the result object contains various information for computing the Sobol indices. For instance, the model simulation data (SimData) for each simulation using a set of parameter samples is stored in the SimData field of the property. This field is an array of SimData objects.
sobolResults.SimulationInfo.SimData
SimBiology SimData Array : 1000-by-7 Index: Name: ModelName: DataCount: 1 - Tumor Growth Model 1 2 - Tumor Growth Model 1 3 - Tumor Growth Model 1 ... 7000 - Tumor Growth Model 1
You can find out if any model simulation failed during the computation by checking the ValidSample field of SimulationInfo. In this example, the field shows no failed simulation runs.
all(sobolResults.SimulationInfo.ValidSample)
ans = 1×7 logical array
1 1 1 1 1 1 1
SimulationInfo.ValidSample is a table of logical values. It has the same size as SimulationInfo.SimData. If ValidSample indicates that any simulations failed, you can get more information about those simulation runs and the samples used for those runs by extracting information from the corresponding column of SimulationInfo.SimData. Suppose that the fourth column contains one or more failed simulation runs. Get the simulation data and sample values used for that simulation using getSimulationResults.
[samplesUsed,sd,validruns] = getSimulationResults(sobolResults,4);
You can add custom expressions as observables and compute Sobol indices for the added observables. For example, you can compute the Sobol indices for the maximum tumor weight by defining a custom expression as follows.
% Suppress an information warning that is issued during simulation. warnSettings = warning('off', 'SimBiology:sbservices:SB_DIMANALYSISNOTDONE_MATLABFCN_UCON'); % Add the observable expression. sobolObs = addobservable(sobolResults,'Maximum tumor_weight','max(tumor_weight)','Units','gram');
Plot the computed simulation results showing the 90% quantile region.
h2 = plotData(sobolObs,ShowMedian=true,ShowMean=false); h2.Position(:) = [100 100 1280 800];
![Figure contains 2 axes objects. Axes object 1 with ylabel Maximum tumor_weight contains 12 objects of type line, patch. One or more of the lines displays its values using only markers These objects represent model simulation, 90.0% region, median value. Axes object 2 with xlabel time, ylabel [Tumor Growth].tumor_weight contains 12 objects of type line, patch. These objects represent model simulation, 90.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_06.png)
You can also remove the observable by specifying its name.
gsaNoObs = removeobservable(sobolObs,'Maximum tumor_weight');Restore the warning settings.
warning(warnSettings);
Input Arguments
SimBiology model, specified as a SimBiology model object.
Names of model parameters, species, or compartments, specified as a character vector, string, string vector, or cell array of character vectors.
Example: ["k1","k2"]
Data Types: char | string | cell
Model responses, specified as a character vector, string, string vector, or cell
array of character vectors. Specify the names of species, parameters, compartments, or
observables.
Example: ["tumor_growth"]
Data Types: char | string | cell
Source for drawing samples, specified as a SimBiology.Scenarios object.
You must combine entries of the object elementwise.
Entries must be independent random variables. If there are multiple entries, they must be uncorrelated.
SamplingMethodof any entry must not becopula.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: sobolResults =
sbiosobol(modelObj,params,observables,'ShowWaitbar',true) specifies to show a
simulation progress bar.
Parameter bounds, specified as a numeric matrix with two columns. The first column contains
the lower bounds and the second column contains the upper
bounds. The number of rows must be equal to the number of
parameters in params.
If a parameter has a nonzero value, the default bounds are ±10% of the value. If the
parameter value is zero, the default bounds are [0 1].
Example: [0.5 5]
Data Types: double
Doses to use during model simulations, specified as a ScheduleDose or
RepeatDose object or a vector of
dose objects.
Variants to apply before model simulations, specified as a variant object or vector of variant objects.
When you specify multiple variants with duplicate specifications for a property's value, the last occurrence for the property value in the array of variants is used during simulation.
Number of samples to compute Sobol indices, specified as the comma-separated pair
consisting of 'NumberSamples' and a positive integer. The function
requires (number of input model simulations to compute the first- and total-order
Sobol indices.params + 2) *
NumberSamples
Data Types: double
Probability distributions used to draw samples, specified as a
prob.ProbabilityDistribution object or vector of these objects.
Specify a scalar prob.ProbabilityDistribution or vector of length
N, where N is the number of input parameters. You
can create distribution objects to sample from various distributions, such as uniform,
normal, or lognormal distributions, using makedist (Statistics and Machine Learning Toolbox).
If you specify a scalar prob.ProbabilityDistribution object, and there are multiple input parameters, sbiosobol uses the same distribution object to draw samples for each parameter.
You cannot specify this argument together with Bounds.
You cannot specify this argument when a SimBiology.Scenarios object is an input.
Method to generate parameter samples, specified as a character vector or string. Valid options are:
'Sobol'— Use the low-discrepancy Sobol sequence to generate samples.'Halton'— Use the low-discrepancy Halton sequence to generate samples.'lhs'— Use the low-discrepancy Latin hypercube samples.'random'— Use uniformly distributed random samples.
Data Types: char | string
Options for the sampling method, specified as a scalar struct. The options differ depending on
the sampling method: sobol, halton, or
lhs.
For sobol and halton, specify each field name and value
of the structure according to each name-value argument of the sobolset (Statistics and Machine Learning Toolbox) or haltonset (Statistics and Machine Learning Toolbox) function. SimBiology uses the
default value of 1 for the Skip argument for both
methods. For all other name-value arguments, the software uses the same default values of
sobolset or haltonset. For instance, set up a
structure for the Leap and Skip options with
nondefault values as
follows.
s1.Leap = 50; s1.Skip = 0;
For lhs, there are three samplers that support different sampling options.
If you specify a covariance matrix, SimBiology uses
lhsnorm(Statistics and Machine Learning Toolbox) for sampling.SamplingOptionsargument is not allowed.Otherwise, use the field name
UseLhsdesignto select a sampler.If the value is
true, SimBiology useslhsdesign(Statistics and Machine Learning Toolbox). You can use the name-value arguments oflhsdesignto specify the field names and values.If the value is
false(default), SimBiology uses a nonconfigurable Latin hypercube sampler that is different fromlhsdesign. This sampler does not require Statistics and Machine Learning Toolbox™.SamplingOptionscannot contain any other options, exceptUseLhsdesign.
For instance, set up a structure to use lhsdesign with the Criterion and Iterations options.
s2.UseLhsdesign = true;
s2.Criterion = "correlation";
s2.Iterations = 10;You cannot specify this argument when a SimBiology.Scenarios
object is an input.
Simulation stop time, specified as a nonnegative scalar. If you specify neither
StopTime nor OutputTimes, the function uses
the stop time from the active configuration set of the model. You cannot specify both
StopTime and OutputTimes.
Data Types: double
Simulation output times, specified as the comma-separated pair consisting of
'OutputTimes' and a numeric vector. The function computes the
Sobol indices at these output time points. You cannot specify both
StopTime and OutputTimes. By default, the
function uses the output times of the first model simulation.
Example: [0 1 2 3.5 4 5 5.5]
Data Types: double
Flag to run model simulations in parallel, specified as true or
false. When the value is true and Parallel Computing Toolbox™ is available, the function runs simulations in parallel.
Data Types: logical
Flag to turn on model acceleration, specified as true or
false.
Data Types: logical
Method for interpolation of model responses to a common set of output times, specified as a character vector or string. The valid options follow.
Data Types: char | string
Flag to show the progress of model simulations by displaying a progress bar,
specified as the comma-separated pair consisting of 'ShowWaitbar'
and true or false. By default, no wait bar is
displayed.
Data Types: logical
Output Arguments
Results containing the first- and total-order Sobol indices, returned as a SimBiology.gsa.Sobol object. The object also contains the parameter sample
values and model simulation data used to compute the Sobol indices.
The results object can contain a significant amount of
simulation data (SimData). The size of the object exceeds (1 + number of observables) *
number of output time points * (2 + number of parameters) * number of samples * 8
bytes. For example, if you have one observable, 500 output time points, 8 parameters, and
100,000 samples, the object size is (1 + 1) * 500 * (2 + 8) * 100000 * 8
bytes = 8 GB. If you need to save such large objects, use this syntax:
save(fileName,variableName,'-v7.3');More About
sbiosobol implements the Saltelli method [1] to compute Sobol
indices.
Consider a SimBiology model response Y expressed as a mathematical model , where Xi is a model parameter
and i = 1,…,k.
The first-order Sobol index (Si) gives the fraction
of the overall response variance V(Y) that can be
attributed to variations in Xi alone.
Si is defined as follows.
The total-order Sobol index (STi) gives the fraction
of the overall response variance V(Y) that can be
attributed to any joint parameter variations that include variations of
Xi.
STi is defined as follows.
To compute individual values for Y corresponding to samples of parameters X1, X1, …, Xk, consider two independent sampling matrices A and B.
n is the sample size. Each row of the matrices A and B corresponds to one parameter sample set, which is a single realization of model parameter values.
Estimates for Si and
STi are obtained from model simulation
results using sample values from the matrices A, B,
and , which is a matrix where all columns are from A except
the ith column, which is from B for i = 1, 2,
…, params.
The formulas to approximate the first- and total-order Sobol indices are as follows.
f(A), f(B), and are the model simulation results using the parameter sample values from
matrices A, B, and .
The matrix A corresponds to the ParameterSamples property of the Sobol results object (resultsObj.ParameterSamples). The matrix B corresponds to the SupportSamples property (resultsObj.SimulationInfo.SupportSamples).
The matrices are stored in the SimData structure of the
SimulationInfo property
(resultsObj.SimulationInfo.SimData). The size of
SimulationInfo.SimData is
NumberSamples-by-params +
2, where NumberSamples is the number of samples and param is the number of input parameters. The number of columns is
2 + params because the first column of
SimulationInfo.SimData contains the model simulation results using
the sample matrix A. The second column contains simulation results using
SupportSamples, which is another sample matrix
B. The rest of the columns contain simulation results using , , …, , …, . See getSimulationResults to retrieve the model simulation results and samples
for a specified ith index () from the SimulationInfo.SimData array.
References
[1] Saltelli, Andrea, Paola Annoni, Ivano Azzini, Francesca Campolongo, Marco Ratto, and Stefano Tarantola. “Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index.” Computer Physics Communications 181, no. 2 (February 2010): 259–70. https://doi.org/10.1016/j.cpc.2009.09.018.
Version History
Introduced in R2020a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)