Specifying Custom Inertias
Key Inertia Conventions
Simscape Multibody software adopts a number of conventions in its inertia definitions. Take note of these as they may impact your inertia calculations if you perform them manually. The conventions may also bear on what additional processing, if any, your inertia data needs—for example, if it was sourced from a CAD application or other third-party software. In particular:
The products of inertia are defined using a negated convention, one with a minus sign inserted, explicitly, in the mass integrals. An alternate convention exists in which a minus sign does not accompany the mass integrals. Recall that the products of inertia are the off-diagonal elements of the inertia matrix.
The center of mass is defined with respect to the local reference frame of the block. In solids with imported CAD shapes, this frame is generally that assumed by your CAD application in its inertia calculations. It is possible, however, to modify a solid geometry file so that the two frames no longer match.
Inertia Matrix Definitions
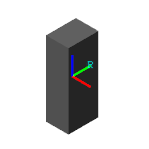
The inertia matrix captures the spatial distribution of matter about a local frame referred to here as the inertia frame of resolution. This frame is labeled I in the figure. Its axes are parallel to those of the local reference frame, associated with frame port R and correspondingly labeled R. However, its origin coincides instead with the local center of mass.

The inertia matrix comprises the moments and products of inertia. The moments of inertia occupy the diagonal matrix positions and measure the dispersion, or spread, of the mass distribution about the axes of the inertia frame of resolution. The greater the spread about an axis, the larger the moment of inertia corresponding to that axis.
The products of inertia occupy the off-diagonal positions and measure the asymmetry of the mass distribution with respect to the planes of the inertia frame of resolution. The greater the asymmetry about a plane, the larger the products of inertia associated with any axis in that plane. The figure illustrates these relationships.

The Inertia Equations
The matrix is symmetric with respect to the main diagonal line: off-diagonal elements whose indices are reciprocals of each other share the same value. This constraint reduces the number of unique products of inertia from the original six (all those in off-diagonal positions) to the three that you must specify in a block (those with a unique combination of indices):
The products of inertia, Iij, are defined using the prevalent, negated, convention adopted by a number of CAD applications:
where ρ is mass density, v is volume, and V is the total volume of integration. The x, y, and z coordinates are the Cartesian components of the distance vector spanning from the center of mass to an infinitesimal element of mass ρdv. The moments of inertia, Iii, are similarly defined:
When applied to simple shapes such as cylindrical shells and rectangular beams, these definitions give rise to well-known algebraic equations that are often published in standard engineering tables. You can reference such tables when specifying the inertia parameters explicitly. The complete inertia matrix, according to the Simscape Multibody convention, is:
Principal Axes of Inertia
The moments of inertia are by definition positive numbers. However, the products of inertia can be either positive, negative, or zero. They are zero if the axes of the inertia frame of resolution happen to coincide with the principal axes of inertia. The moments of inertia are then called the principal moments of inertia and the inertia matrix is said to be diagonal:
The number of nontrivial inertia matrix elements that you must specify is in this case reduced to three—the principal moments of inertia. For this reason, the principal axes of inertia can be a convenient frame in which to specify the inertia matrix elements. This is the inertia frame of resolution assumed in the highly symmetrical preset shapes of the solid blocks.
The same, however, is not generally true of Extruded Solid or Revolved Solid solid shapes, nor is it of those imported via STEP or STL files. In Extruded Solid and Revolved Solid shapes, the frame placement depends closely on how you define the geometrical cross-sections. In imported shapes, it depends on how, relative to the local zero coordinate, the part geometries were modeled.
As a best practice, always consider the placement of the inertia frame of resolution when specifying the elements of the inertia matrix explicitly, particularly when using a solid block. The frame position is always that of the center of mass, but its orientation relative to a solid geometry, when using a solid block, may not always coincide with the principal axes of inertia.
Try It: Specify a Custom Inertia
Consider the rectangular beam shown in the figure. Determine its mass, center of mass, moments of inertia, and products of inertia. Specify the calculated parameters explicitly in a Brick Solid block using a Custom inertia parameterization.
Material and Dimensions. Assume a construction of aluminum and a corresponding mass density of 0.09754 lbm/in^3. Use the beam dimensions:
Width x = 3 in
Height y = 4 in
Length z = 10 in
Prepare the Beam Model. Add a Brick Solid block to a Simscape Multibody model. In the Brick Solid block dialog box, specify the beam geometry: set the Geometry > Dimensions parameter to [3 4 10] in. This array corresponds to the beam dimensions [x y z].
The geometry type affects the placement of the local reference frame (R) and therefore the inertia calculations themselves. In the visualization toolstrip, click the Toggle visibility of frames button. Frame R is located at the center of mass and its axes are parallel to the beam dimensions (x, y, and z).
Specify the Inertia Parameters. Calculate the inertia parameters from the density and dimensions of the beam. Then, specify the calculated values in the Inertia section of the Brick Solid block parameters:
Mass — Product of mass density (ρ) and volume (x · y · z):
Center of Mass — Centroid coordinates with respect to the local reference frame (R):
Moments of Inertia — From standard expressions with respect to the inertia frame of resolution (I):
Products of Inertia — From symmetry with respect to the inertia frame of resolution (I):
CAD as an Inertia Data Source
CAD applications often provide the inertia data for your part models. Examples include SolidWorks software, through its Mass Properties tool, and Onshape software, through its version of the same tool. You can reference this data and specify it manually in the Simscape Multibody environment.
Alternate Inertia Conventions
Some CAD applications, SolidWorks among them, use an alternate inertia convention to define the elements of the inertia matrix. This convention removes the minus sign from the product-of-inertia definitions. The Iyz product of inertia, for example, becomes:
If your source of inertia data adopts this convention, you must explicitly negate the products of inertia before specifying their values in the Simscape Multibody environment. As an example, consider a SolidWorks inertia matrix given as:
To correctly specify the matrix elements in the Simscape Multibody environment, you must treat them as follows:
CAD Import as an Alternative
Rather than reference the inertia data in a CAD assembly model, you can import that model into the Simscape Multibody environment. CAD import is based on the smimport function, which parses a multibody description file in XML format and generates an equivalent block diagram with all block parameters prespecified—inertia parameters included.
You must export your CAD model in a valid XML format, meaning one that conforms to the Simscape Multibody XML schema, before you can import it. This option may suit you only if you have a complete CAD assembly model. For individual CAD parts, use the STEP file import feature of the solid block and set the Inertia > Type parameter to Calculate from Geometry.
For more information, see Convert CAD Assembly into Simscape Multibody Model.
Try It: Reference a SolidWorks Model
Determine the inertia parameters for the L-beam shape shown in the figure. Then, specify them explicitly in a solid block by setting the inertia parameterization to Custom. Use the mass properties data provided in this example for a SolidWorks model of the beam.
Open the Solid Model. At the MATLAB® command prompt, enter
openExample("sm/DocLBeamInertiaExample"). A
simple model opens with a File Solid
block representing the L-beam solid. Open the File
Solid block and explore its
Geometry parameters. The beam geometry is
imported from a STEP file previously exported from a SolidWorks model.
This geometry is shown in the figure.

In the visualization pane, click the Toggle visibility of frames button. The visualization pane shows two frames, one labeled R and the other I.
Frame R is the local reference frame of the solid. It coincides with what SolidWorks users refer to as the output coordinate system of the part model. This frame is located at the lower corner of the L-shape on one of the two longitudinal ends of the beam. You must specify the center of mass relative to this frame.
Frame I is a custom solid frame included for your convenience. This frame coincides with the inertia frame of resolution. Its origin is at the center of mass and its axes are parallel to those of the local reference frame. You must specify the moments and products of inertia relative to this frame.
Review the SolidWorks Data. The SolidWorks model provides for the L-beam part the following mass properties data:
Mass properties of l_beam_solid
Configuration: Default
Coordinate system: -- default --
Density = 0.10 pounds per cubic inch
Mass = 2.19 pounds
Volume = 22.41 cubic inches
Surface area = 101.91 square inches
Center of mass: ( inches )
X = 0.58
Y = 1.08
Z = 5.00
Principal axes of inertia and principal moments of inertia:
( pounds * square inches )
Taken at the center of mass.
Ix = ( 0.00, 0.00, 1.00) Px = 2.49
Iy = ( 0.38, -0.92, 0.00) Py = 18.65
Iz = ( 0.92, 0.38, 0.00) Pz = 20.35
Moments of inertia: ( pounds * square inches )
Taken at the center of mass and aligned with
the output coordinate system.
Lxx = 20.10 Lxy = -0.60 Lxz = 0.00
Lyx = -0.60 Lyy = 18.89 Lyz = 0.00
Lzx = 0.00 Lzy = 0.00 Lzz = 2.49
Moments of inertia: ( pounds * square inches )
Taken at the output coordinate system.
Ixx = 77.40 Ixy = 0.76 Ixz = 6.33
Iyx = 0.76 Iyy = 74.39 Iyz = 11.79
Izx = 6.33 Izy = 11.79 Izz = 5.76The data includes the coordinates of the center of mass with respect to the “output coordinate system.” This coordinate system coincides with the local reference frame (R) of the corresponding Simscape Multibody solid.
The data includes also a matrix with the moments and products of inertia “taken at the center of mass and aligned with the output coordinate system.” This coordinate system coincides with the inertia frame of resolution (I) of the Simscape Multibody solid.
Specify the Inertia Parameters. Expand the Inertia parameters section of the File Solid block dialog box. Then, change the inertia parameterization by setting the Inertia > Type parameter to Custom. The complete set of inertia parameters appears for you to specify.
Set the Mass parameter to
2.19 lb. This is the mass corresponding to the density of aluminum.Set the Center of Mass parameter to
[0.58 1.08 5.00] in. These are the [x y z] coordinates of the center of mass shown in the SolidWorks report.Set the Moments of Inertia parameter to
[20.10 18.89 2.49] lbm*in^2. These are the [Lxx Lyy Lzz] moments of inertia shown in the SolidWorks report.Set the Products of Inertia parameter to
[0 0 0.6] lbm*in^2. These are the negated [Lyz Lzx Lxy ] products of inertia shown in the SolidWorks report.
Automatic Inertia Calculation
The solid blocks provides an option to automatically compute the majority of inertia parameters given a solid geometry. This option, available from the Inertia > Type drop-down list and by default on, requires you to specify only the geometry parameters and either the mass or mass density.
The block uses the geometry and mass parameters to compute the remaining inertia parameters—the center of mass, moments of inertia, and products of inertia—relative to the appropriate frame of reference. The calculations are based on the assumption of a mass density that is constant and uniform.
You can view the calculation results inside the solid block, in an expandable section named Display Inertia. The center of mass is given relative to the local reference frame (R), and the moments and products of inertia relative to the inertia frame of resolution (I). These are the same frames relative to which you might specify these parameters.
Try It: Display the Calculated Inertia Results
Configure the File Solid block of the
DocLBeamInertiaExample model to calculate the inertia
parameters from the solid geometry and its mass density. Then, view the
calculated parameters.
In the dialog box of the File Solid block, switch the Inertia > Type parameter to
Calculate from Geometry. A Display Inertia node appears below the Density parameter.Set the Density parameter to
0.09754 lbm/in^2. This value corresponds to a solid of aluminum construction and it is the same assumed in the SolidWorks data provided in Review the SolidWorks Data.Expand the Display Inertia node and click the Update button. The inertia parameters under Display Inertia are populated with the calculated values. Compare them to the values provided in the SolidWorks mass properties data.
