anova2

Two-way analysis of variance

Syntax

p = anova2(y,reps)

p = anova2(y,reps,displayopt)

[p,tbl] = anova2(___)

[p,tbl,stats] = anova2(___)

Description

anova2 performs two-way analysis of variance (ANOVA) with balanced designs. To perform two-way ANOVA with unbalanced designs, see anovan.

p = anova2(y,reps) returns the p-values for a balanced two-way ANOVA for comparing the means of two or more columns and two or more rows of the observations in y.

reps is the number of replicates for each combination of factor groups, which must be constant, indicating a balanced design. For unbalanced designs, use anovan. The anova2 function tests the main effects for column and row factors and their interaction effect. To test the interaction effect, reps must be greater than 1.

anova2 also displays the standard ANOVA table.

p = anova2(y,reps,displayopt) enables the ANOVA table display when displayopt is 'on' (default) and suppresses the display when displayopt is 'off'.

[p,tbl] = anova2(___) returns the ANOVA table (including column and row labels) in cell array tbl. To copy a text version of the ANOVA table to the clipboard, select Edit > Copy Text menu.

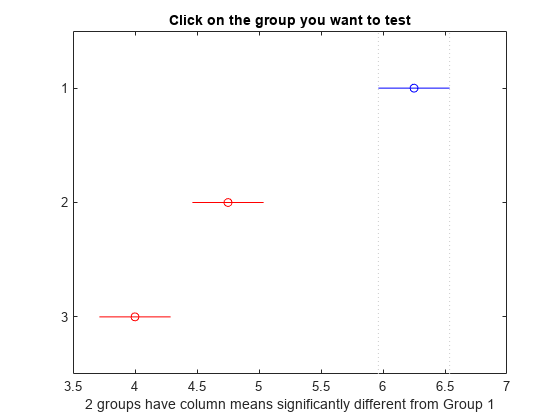
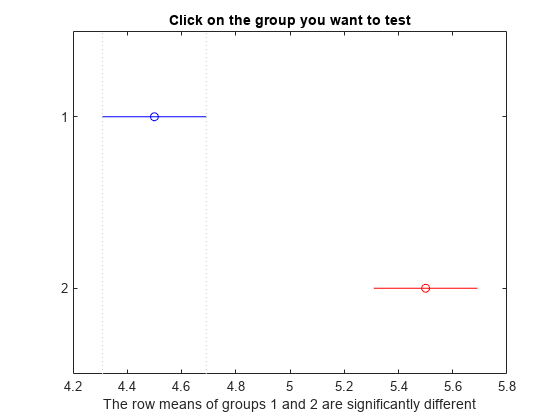
[p,tbl,stats] = anova2(___) returns a stats structure, which you can use to perform a multiple comparison test. A multiple comparison test enables you to determine which pairs of group means are significantly different. To perform this test, use multcompare, providing the stats structure as input.

Examples

Two-Way ANOVA

Load the sample data.

load popcorn
popcorn

popcorn = 6×3

    5.5000    4.5000    3.5000
    5.5000    4.5000    4.0000
    6.0000    4.0000    3.0000
    6.5000    5.0000    4.0000
    7.0000    5.5000    5.0000
    7.0000    5.0000    4.5000

The data is from a study of popcorn brands and popper types (Hogg 1987). The columns of the matrix popcorn are brands, Gourmet, National, and Generic, respectively. The rows are popper types, oil and air. In the study, researchers popped a batch of each brand three times with each popper, that is, the number of replications is 3. The first three rows correspond to the oil popper, and the last three rows correspond to the air popper. The response values are the yield in cups of popped popcorn.

Perform a two-way ANOVA. Save the ANOVA table in the cell array tbl for easy access to results.

[p,tbl] = anova2(popcorn,3);

The column Prob>F shows the p-values for the three brands of popcorn (0.0000), the two popper types (0.0001), and the interaction between brand and popper type (0.7462). These values indicate that popcorn brand and popper type affect the yield of popcorn, but there is no evidence of an interaction effect of the two.

Display the cell array containing the ANOVA table.

tbl

tbl=6×6 cell array
    {'Source'     }    {'SS'     }    {'df'}    {'MS'      }    {'F'       }    {'Prob>F'    }
    {'Columns'    }    {[15.7500]}    {[ 2]}    {[  7.8750]}    {[ 56.7000]}    {[7.6790e-07]}
    {'Rows'       }    {[ 4.5000]}    {[ 1]}    {[  4.5000]}    {[ 32.4000]}    {[1.0037e-04]}
    {'Interaction'}    {[ 0.0833]}    {[ 2]}    {[  0.0417]}    {[  0.3000]}    {[    0.7462]}
    {'Error'      }    {[ 1.6667]}    {[12]}    {[  0.1389]}    {0x0 double}    {0x0 double  }
    {'Total'      }    {[     22]}    {[17]}    {0x0 double}    {0x0 double}    {0x0 double  }

Store the F-statistic for the factors and factor interaction in separate variables.

Fbrands = tbl{2,5}

Fbrands = 56.7000

Fpoppertype = tbl{3,5}

Fpoppertype = 32.4000

Finteraction = tbl{4,5}

Finteraction = 0.3000

Multiple Comparisons for Two-Way ANOVA

Load the sample data.

load popcorn
popcorn

popcorn = 6×3

    5.5000    4.5000    3.5000
    5.5000    4.5000    4.0000
    6.0000    4.0000    3.0000
    6.5000    5.0000    4.0000
    7.0000    5.5000    5.0000
    7.0000    5.0000    4.5000

The data is from a study of popcorn brands and popper types (Hogg 1987). The columns of the matrix popcorn are brands (Gourmet, National, and Generic). The rows are popper types oil and air. The first three rows correspond to the oil popper, and the last three rows correspond to the air popper. In the study, researchers popped a batch of each brand three times with each popper. The values are the yield in cups of popped popcorn.

Perform a two-way ANOVA. Also compute the statistics that you need to perform a multiple comparison test on the main effects.

[~,~,stats] = anova2(popcorn,3,"off")

stats = struct with fields:
      source: 'anova2'
     sigmasq: 0.1389
    colmeans: [6.2500 4.7500 4]
        coln: 6
    rowmeans: [4.5000 5.5000]
        rown: 9
       inter: 1
        pval: 0.7462
          df: 12

The stats structure includes

• The mean squared error (sigmasq)

• The estimates of the mean yield for each popcorn brand (colmeans)

• The number of observations for each popcorn brand (coln)

• The estimate of the mean yield for each popper type (rowmeans)

• The number of observations for each popper type (rown)

• The number of interactions (inter)

• The p-value that shows the significance level of the interaction term (pval)

• The error degrees of freedom (df).

Perform a multiple comparison test to see if the popcorn yield differs between pairs of popcorn brands (columns).

c1 = multcompare(stats);

Note: Your model includes an interaction term.  A test of main effects can be 
difficult to interpret when the model includes interactions.

The figure shows the multiple comparisons of the means. By default, the group 1 mean is highlighted and the comparison interval is in blue. Because the comparison intervals for the other two groups do not intersect with the intervals for the group 1 mean, they are highlighted in red. This lack of intersection indicates that both means are different than group 1 mean. Select other group means to confirm that all group means are significantly different from each other.

Display the multiple comparison results in a table.

tbl1 = array2table(c1,"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"])

tbl1=3×6 table
    Group A    Group B    Lower Limit    A-B     Upper Limit     P-value  
    _______    _______    ___________    ____    ___________    __________

       1          2         0.92597       1.5       2.074       4.1188e-05
       1          3           1.676      2.25       2.824       6.1588e-07
       2          3         0.17597      0.75       1.324         0.011591

The first two columns of c1 show the groups that are compared. The fourth column shows the difference between the estimated group means. The third and fifth columns show the lower and upper limits for 95% confidence intervals for the true mean difference. The sixth column contains the p-value for a hypothesis test that the corresponding mean difference is equal to zero. All p-values are very small, which indicates that the popcorn yield differs across all three brands.

Perform a multiple comparison test to see the popcorn yield differs between the two popper types (rows).

c2 = multcompare(stats,"Estimate","row");

Note: Your model includes an interaction term.  A test of main effects can be 
difficult to interpret when the model includes interactions.

tbl2 = array2table(c2,"VariableNames", ...
    ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"])

tbl2=1×6 table
    Group A    Group B    Lower Limit    A-B    Upper Limit     P-value  
    _______    _______    ___________    ___    ___________    __________

       1          2         -1.3828      -1      -0.61722      0.00010037

The small p-value indicates that the popcorn yield differs between the two popper types (air and oil). The figure shows the same results. The disjoint comparison intervals indicate that the group means are significantly different from each other.

Input Arguments

y — Sample data

matrix

Sample data, specified as a matrix. The columns correspond to groups of one factor, and the rows correspond to the groups of the other factor and the replications. Replications are the measurements or observations for each combination of groups (levels) of the row and column factor. For example, in the following data the row factor A has three levels, column factor B has two levels, and there are two replications (reps = 2). The subscripts indicate row, column, and replication, respectively.

$$\begin{array}{c}\begin{array}{cc}B=1& B=2\end{array}\\ \left[\begin{array}{cc}{y}_{111}& y_{121}\\ y_{112}& y_{122}\\ y_{211}& y_{221}\\ y_{212}& y_{222}\\ y_{311}& y_{321}\\ y_{312}& y_{322}\end{array}\right]\end{array}\begin{array}{c}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\}A=1\\ \begin{array}{c}\\ \end{array}\}A=2\\ \begin{array}{c}\\ \end{array}\}A=3\end{array}\end{array}$$

Data Types: single | double

reps — Number of replications

1 (default) | an integer number

Number of replications for each combination of groups, specified as an integer number. For example, the following data has two replications (reps = 2) for each group combination of row factor A and column factor B.

$$\begin{array}{c}\begin{array}{cc}B=1& B=2\end{array}\\ \left[\begin{array}{cc}{y}_{111}& y_{121}\\ y_{112}& y_{122}\\ y_{211}& y_{221}\\ y_{212}& y_{222}\\ y_{311}& y_{321}\\ y_{312}& y_{322}\end{array}\right]\end{array}\begin{array}{c}\\ \begin{array}{c}\begin{array}{c}\\ \end{array}\}A=1\\ \begin{array}{c}\\ \end{array}\}A=2\\ \begin{array}{c}\\ \end{array}\}A=3\end{array}\end{array}$$

• When reps is 1 (default), anova2 returns two p-values in vector p:

  • The p-value for the null hypothesis that all samples from factor B (i.e., all column samples in y) are drawn from the same population.

  • The p-value for the null hypothesis, that all samples from factor A (i.e., all row samples in y) are drawn from the same population.

• When reps is greater than 1, anova2 also returns the p-value for the null hypothesis that factors A and B have no interaction (i.e., the effects due to factors A and B are additive).

Example: p = anova(y,3) specifies that each combination of groups (levels) has three replications.

Data Types: single | double

displayopt — Indicator to display the ANOVA table

'on' (default) | 'off'

Indicator to display the ANOVA table as a figure, specified as 'on' or 'off'.

Output Arguments

p — p-value

scalar value

p-value for the F-test, returned as a scalar value. A small p-value indicates that the results are statistically significant. Common significance levels are 0.05 or 0.01. For example:

• A sufficiently small p-value for the null hypothesis for group means of row factor A suggests that at least one row-sample mean is significantly different from the other row-sample means; i.e., there is a main effect due to factor A

• A sufficiently small p-value for the null hypothesis for group (level) means of column factor B suggests that at least one column-sample mean is significantly different from the other column-sample means; i.e., there is a main effect due to factor B.

• A sufficiently small p-value for combinations of groups (levels) of factors A and B suggests that there is an interaction between factors A and B.

tbl — ANOVA table

cell array

ANOVA table, returned as a cell array. tbl has six columns.

Column name	Definition
source	Source of the variability.
SS	Sum of squares due to each source.
df	Degrees of freedom associated with each source.
MS	Mean squares for each source, which is the ratio SS/df.
F	F-statistic, which is the ratio of the mean squares.
Prob>F	p-value, which is the probability that the F-statistic can take a value larger than the computed test-statistic value. anova2 derives this probability from the cdf of the F-distribution.

The rows of the ANOVA table show the variability in the data, divided by the source into three or four parts, depending on the value of reps.

Row	Definition
Columns	Variability due to the differences among the column means
Rows	Variability due to the differences among the row means
Interaction	Variability due to the interaction between rows and columns (if reps is greater than its default value of 1)
Error	Remaining variability not explained by any systematic source

Data Types: cell

stats — Statistics for multiple comparison test

structure

Statistics for multiple comparisons tests, returned as a structure. Use multcompare to perform multiple comparison tests, supplying stats as an input argument. stats has nine fields.

Field	Definition
source	Source of the stats output
sigmasq	Mean squared error
colmeans	Estimated values of the column means
coln	Number of observations for each group in columns
rowmeans	Estimated values of the row means
rown	Number of observations for each group in rows
inter	Number of interactions
pval	p-value for the interaction term
df	Error degrees of freedom (reps — 1)*r*c where reps is the number of replications and c and r are the number of groups in factors, respectively.

Data Types: struct

References

[1] Hogg, R. V., and J. Ledolter. Engineering Statistics. New York: MacMillan, 1987.

Version History

Introduced before R2006a