ClassificationTree
Binary decision tree for multiclass classification
Description
A ClassificationTree object represents a
decision tree with binary splits for classification. An object of this class can predict
responses for new data using predict. The object contains the data used
for training, so it can also compute resubstitution predictions using resubPredict.
Creation
Create a ClassificationTree object by using fitctree.
Properties
Tree Properties
This property is read-only.
Categorical splits, returned as an n-by-2 cell array, where
n is the number of categorical splits in
tree. Each row in CategoricalSplit gives
left and right values for a categorical split. For each branch node with categorical
split j based on a categorical predictor variable
z, the left child is chosen if z is in
CategoricalSplit(j,1) and the right child is chosen if
z is in CategoricalSplit(j,2). The splits are
in the same order as nodes of the tree. Nodes for these splits can be found by running
cuttype and selecting 'categorical' cuts from
top to bottom.
Data Types: cell
This property is read-only.
Numbers of the child nodes for each node in the tree, returned as an
n-by-2 array, where n is the number of nodes.
Leaf nodes have child node 0.
Data Types: double
This property is read-only.
Class counts for the nodes in tree, returned as an
n-by-k array, where n is
the number of nodes and k is the number of classes. For any node
number i, the class counts ClassCount(i,:) are
counts of observations (from the data used in fitting the tree) from each class
satisfying the conditions for node i.
Data Types: double
This property is read-only.
Class probabilities for the nodes in tree, returned as an
n-by-k array, where n is
the number of nodes and k is the number of classes. For any node
number i, the class probabilities
ClassProbability(i,:) are the estimated probabilities for each
class for a point satisfying the conditions for node i.
Data Types: double
This property is read-only.
Categories used at branches in tree, returned as an
n-by-2 cell array, where n is the number of
nodes. For each branch node i based on a categorical predictor
variable X, the left child is chosen if X is among
the categories listed in CutCategories{i,1}, and the right child is
chosen if X is among those listed in
CutCategories{i,2}. Both columns of
CutCategories are empty for branch nodes based on continuous
predictors and for leaf nodes.
CutPoint contains the cut points for
'continuous' cuts, and CutCategories contains
the set of categories.
Data Types: cell
This property is read-only.
Values used as cut points in tree, returned as an
n-element vector, where n is the number of
nodes. For each branch node i based on a continuous predictor
variable X, the left child is chosen if
X<CutPoint(i) and the right child is chosen if
X>=CutPoint(i). CutPoint is
NaN for branch nodes based on categorical predictors and for leaf
nodes.
CutPoint contains the cut points for
'continuous' cuts, and CutCategories contains
the set of categories.
Data Types: double
This property is read-only.
Names of the variables used for branching in each node in tree, returned as an n-element cell array, where n is the number of nodes. These variables are sometimes known as cut variables. For leaf nodes, CutPredictor contains an empty character vector.
CutPoint contains the cut points for 'continuous' cuts, and CutCategories contains the set of categories.
Data Types: cell
This property is read-only.
Indices of variables used for branching in each node in tree,
returned as an n-element array, where n is the
number of nodes. For more information, see CutPredictor.
Data Types: double
This property is read-only.
Type of cut at each node in tree, returned as an
n-element cell array, where n is the number of
nodes. For each node i, CutType{i} is:
'continuous'— If the cut is defined in the formX < vfor a variableXand cut pointv.'categorical'— If the cut is defined by whether a variableXtakes a value in a set of categories.''— Ifiis a leaf node.
CutPoint contains the cut points for
'continuous' cuts, and CutCategories contains
the set of categories.
Data Types: cell
This property is read-only.
Indicator of branch nodes, returned as an n-element logical vector that is true for each branch node and false for each leaf node of tree.
Data Types: logical
This property is read-only.
Parameters used in training tree, returned as a
TreeParams object. To display all parameter
values, enter tree.ModelParameters. To access a
particular parameter, use dot notation.
This property is read-only.
Name of most probably class in each node of tree, returned as a cell array with n elements, where n is the number of nodes in the tree. Each element of this array is a character vector equal to one of the class names in ClassNames.
Data Types: cell
This property is read-only.
Misclassification probability for each node in tree, returned as an n-element vector, where n is the number of nodes in the tree.
Data Types: double
This property is read-only.
Proportion of observations in original data that satisfy the conditions for each node in tree, returned as an n-element vector, where n is the number of nodes in the tree. The NodeProbability values are adjusted for any prior probabilities assigned to each class.
Data Types: double
This property is read-only.
Impurity of each node in tree, weighted by the node probability, returned as an n-element vector, where n is the number of nodes in the tree. The measure of impurity is the Gini index or deviance for the node, weighted by the node probability. If the tree is grown by twoing, the risk for each node is zero.
Data Types: double
This property is read-only.
Size of the nodes in tree, returned as an n-element vector, where n is the number of nodes in the tree. The size of a node is the number of observations from the data used to create the tree that satisfy the conditions for the node.
Data Types: double
This property is read-only.
The number of nodes in tree, returned as a positive integer.
Data Types: double
This property is read-only.
Number of parents of each node in tree, returned as an n-element integer vector, where n is the number of nodes in the tree. The parent of the root node is 0.
Data Types: double
Alpha values for pruning the tree, returned as a real vector with one element per pruning level. If the pruning level ranges from 0 to M, then PruneAlpha has M + 1 elements sorted in ascending order. PruneAlpha(1) is for pruning level 0 (no pruning), PruneAlpha(2) is for pruning level 1, and so on.
For the meaning of the ɑ values, see How Decision Trees Create a Pruning Sequence.
Data Types: double
Pruning levels of each node in the tree, returned as an integer vector with NumNodes elements. The pruning levels range from 0 (no pruning) to M, where M is the distance between the deepest leaf and the root node.
For details, see Pruning.
Data Types: double
This property is read-only.
Categories used for surrogate splits, returned as an n-element cell
array, where n is the number of nodes in tree.
For each node k, SurrogateCutCategories{k} is a
cell array. The length of SurrogateCutCategories{k} is equal to the
number of surrogate predictors found at this node. Every element of
SurrogateCutCategories{k} is either an empty character vector for
a continuous surrogate predictor, or is a two-element cell array with categories for a
categorical surrogate predictor. The first element of this two-element cell array lists
categories assigned to the left child by this surrogate split and the second element of
this two-element cell array lists categories assigned to the right child by this
surrogate split. The order of the surrogate split variables at each node is matched to
the order of variables in SurrogateCutVar. The optimal-split variable
at this node does not appear. For nonbranch (leaf) nodes,
SurrogateCutCategories contains an empty cell.
Data Types: cell
This property is read-only.
Numeric cut assignments used for surrogate splits in tree, returned as an n-element cell array, where n is the number of nodes in tree. For each node k, SurrogateCutFlip{k} is a numeric vector. The length of SurrogateCutFlip{k} is equal to the number of surrogate predictors found at this node. Every element of SurrogateCutFlip{k} is either zero for a categorical surrogate predictor, or a numeric cut assignment for a continuous surrogate predictor. The numeric cut assignment can be either –1 or +1. For every surrogate split with a numeric cut C based on a continuous predictor variable Z, the left child is chosen if Z<C and the cut assignment for this surrogate split is +1, or if Z≥C and the cut assignment for this surrogate split is –1. Similarly, the right child is chosen if Z≥C and the cut assignment for this surrogate split is +1, or if Z<C and the cut assignment for this surrogate split is –1. The order of the surrogate split variables at each node is matched to the order of variables in SurrogateCutPredictor. The optimal-split variable at this node does not appear. For nonbranch (leaf) nodes, SurrogateCutFlip contains an empty array.
Data Types: cell
This property is read-only.
Numeric values used for surrogate splits in tree, returned as an
n-element cell array, where n is the number of
nodes in tree. For each node k,
SurrogateCutPoint{k} is a numeric vector. The length of
SurrogateCutPoint{k} is equal to the number of surrogate
predictors found at this node. Every element of SurrogateCutPoint{k}
is either NaN for a categorical surrogate predictor, or a numeric cut
for a continuous surrogate predictor. For every surrogate split with a numeric cut
C based on a continuous predictor variable Z,
the left child is chosen if Z<C and SurrogateCutFlip for this surrogate split is
+1, or if Z≥C and
SurrogateCutFlip for this surrogate split is –1. Similarly, the
right child is chosen if Z≥C and SurrogateCutFlip for this surrogate split is
+1, or if Z<C and SurrogateCutFlip for this surrogate split is
–1. The order of the surrogate split variables at each node is matched to the order of
variables returned by SurrogateCutPredictor. The optimal-split
variable at this node does not appear. For nonbranch (leaf) nodes,
SurrogateCutPoint contains an empty cell.
Data Types: cell
This property is read-only.
Names of the variables used for surrogate splits in each node in
tree, returned as an n-element cell array,
where n is the number of nodes in tree. Every
element of SurrogateCutPredictor is a cell array with the names of
the surrogate split variables at this node. The variables are sorted by the predictive
measure of association with the optimal predictor in the descending order, and only
variables with the positive predictive measure are included. The optimal-split variable
at this node does not appear. For nonbranch (leaf) nodes,
SurrogateCutPredictor contains an empty cell.
Data Types: cell
This property is read-only.
Types of surrogate splits at each node in tree, returned as an
n-element cell array, where n is the number of
nodes in tree. For each node k,
SurrogateCutType{k} is a cell array with the types of the
surrogate split variables at this node. The variables are sorted by the predictive
measure of association with the optimal predictor in the descending order, and only
variables with the positive predictive measure are included. The order of the surrogate
split variables at each node is matched to the order of variables in
SurrogateCutPredictor. The optimal-split variable at this node
does not appear. For nonbranch (leaf) nodes, SurrogateCutType
contains an empty cell. A surrogate split type can be either
'continuous' if the cut is defined in the form
Z<V for a variable Z and
cut point V or 'categorical' if the cut is defined
by whether Z takes a value in a set of categories.
Data Types: cell
This property is read-only.
Predictive measures of association for surrogate splits in tree, returned as an n-element cell array, where n is the number of nodes in tree. For each node k, SurrogatePredictorAssociation{k} is a numeric vector. The length of SurrogatePredictorAssociation{k} is equal to the number of surrogate predictors found at this node. Every element of SurrogatePredictorAssociation{k} gives the predictive measure of association between the optimal split and this surrogate split. The order of the surrogate split variables at each node is the order of variables in SurrogateCutPredictor. The optimal-split variable at this node does not appear. For nonbranch (leaf) nodes, SurrogatePredictorAssociation contains an empty cell.
Data Types: cell
Predictor Properties
This property is read-only.
Bin edges for numeric predictors, specified as a cell array of p numeric vectors, where p is the number of predictors. Each vector includes the bin edges for a numeric predictor. The element in the cell array for a categorical predictor is empty because the software does not bin categorical predictors.
The software bins numeric predictors only if you specify the NumBins
name-value argument as a positive integer scalar when training a model with tree learners.
The BinEdges property is empty if the NumBins value
is empty (default).
You can reproduce the binned predictor data Xbinned by using the
BinEdges property of the trained model
mdl.
X = mdl.X; % Predictor data
Xbinned = zeros(size(X));
edges = mdl.BinEdges;
% Find indices of binned predictors.
idxNumeric = find(~cellfun(@isempty,edges));
if iscolumn(idxNumeric)
idxNumeric = idxNumeric';
end
for j = idxNumeric
x = X(:,j);
% Convert x to array if x is a table.
if istable(x)
x = table2array(x);
end
% Group x into bins by using the discretize function.
xbinned = discretize(x,[-inf; edges{j}; inf]);
Xbinned(:,j) = xbinned;
endXbinned contains the bin indices, ranging from 1
to the number of bins, for the numeric predictors. Xbinned values are 0
for categorical predictors. If X contains NaNs, then
the corresponding Xbinned values are NaNs.Data Types: cell
This property is read-only.
Categorical predictor
indices, specified as a vector of positive integers. CategoricalPredictors
contains index values indicating that the corresponding predictors are categorical. The index
values are between 1 and p, where p is the number of
predictors used to train the model. If none of the predictors are categorical, then this
property is empty ([]).
Data Types: single | double
This property is read-only.
Expanded predictor names, returned as a cell array of character vectors.
If the model uses encoding for categorical variables, then
ExpandedPredictorNames includes the names that describe the
expanded variables. Otherwise, ExpandedPredictorNames is the same as
PredictorNames.
Data Types: cell
This property is read-only.
Predictor names, specified as a cell array of character vectors. The order of the
entries in PredictorNames is the same as in the training data.
Data Types: cell
This property is read-only.
Predictor values, returned as a real matrix or table. Each column of
X represents one variable (predictor), and each row represents
one observation.
Data Types: double | table
Response Properties
This property is read-only.
List of the elements in Y with duplicates removed, returned as a
categorical array, cell array of character vectors, character array, logical vector, or
numeric vector. ClassNames has the same data type as the data in the
argument Y. (The software treats string arrays as cell arrays of character
vectors.)
Data Types: double | logical | char | cell | categorical
This property is read-only.
Name of the response variable, returned as a character vector.
Data Types: char
This property is read-only.
Class labels corresponding to the observations in X, returned as
a categorical array, cell array of character vectors, character array, logical vector,
or numeric vector. Each row of Y represents the classification of the
corresponding row of X.
Data Types: single | double | logical | char | string | cell | categorical
Other Data Properties
This property is read-only.
Description of the cross-validation optimization of hyperparameters, returned as a
BayesianOptimization object or a table of
hyperparameters and associated values. This property is nonempty if the
OptimizeHyperparameters name-value argument is nonempty when you
create the model. The value of HyperparameterOptimizationResults
depends on the setting of the Optimizer option in
HyperparameterOptimizationOptions when you create the
model.
"bayesopt"(default) — Object of classBayesianOptimization"gridsearch"or"randomsearch"— Table of hyperparameters used, observed objective function values (cross-validation loss), and rank of observations from lowest (best) to highest (worst)
This property is read-only.
Number of observations in the training data, returned as a positive integer.
NumObservations can be less than the number of rows of input data
when there are missing values in the input data or response data.
Data Types: double
This property is read-only.
Rows of the original predictor data X used for fitting, returned as
an n-element logical vector, where n is the number
of rows of X. If the software uses all rows of X
to create the object, then RowsUsed is an empty array
([]).
Data Types: logical
This property is read-only.
Scaled weights in tree, returned as a numeric vector.
W has length n, the number of rows in the
training data.
Data Types: double
Other Classification Properties
This property is read-only.
Misclassification costs, returned as a square numeric matrix.
Cost has K rows and columns, where
K is the number of classes.
Cost(i,j) is the cost of classifying a point into class
j if its true class is i. The order of the
rows and columns of Cost corresponds to the order of the classes in
ClassNames.
Data Types: double
This property is read-only.
Prior probabilities for each class, returned as a K-element numeric
vector, where K is the number of unique classes in the response. The
order of the elements of Prior corresponds to the order of the
classes in ClassNames.
Data Types: double
Function for transforming scores, specified as a function handle or the name of a built-in
transformation function. "none" means no transformation;
equivalently, "none" means @(x)x. For a list of
built-in transformation functions and the syntax of custom transformation functions, see
ScoreTransform (for
trees) or ScoreTransform (for
ensembles).
Add or change a ScoreTransform function using dot notation:
Mdl.ScoreTransform = "function" % or Mdl.ScoreTransform = @function
Data Types: char | string | function_handle
Object Functions
compact | Reduce size of machine learning model |
compareHoldout | Compare accuracies of two classification models using new data |
crossval | Cross-validate machine learning model |
cvloss | Classification error by cross-validation for classification tree model |
edge | Classification edge for classification tree model |
gather | Gather properties of Statistics and Machine Learning Toolbox object from GPU |
lime | Local interpretable model-agnostic explanations (LIME) |
loss | Classification loss for classification tree model |
margin | Classification margins for classification tree model |
nodeVariableRange | Retrieve variable range of decision tree node |
partialDependence | Compute partial dependence |
plotPartialDependence | Create partial dependence plot (PDP) and individual conditional expectation (ICE) plots |
predict | Predict labels using classification tree model |
predictorImportance | Estimates of predictor importance for classification tree |
prune | Produce sequence of classification subtrees by pruning classification tree |
resubEdge | Resubstitution classification edge for classification tree model |
resubLoss | Resubstitution classification loss for classification tree model |
resubMargin | Resubstitution classification margins for classification tree model |
resubPredict | Classify observations in classification tree by resubstitution |
shapley | Shapley values |
surrogateAssociation | Mean predictive measure of association for surrogate splits in classification tree |
testckfold | Compare accuracies of two classification models by repeated cross-validation |
view | View classification tree |
Examples
Grow a classification tree using the ionosphere data set.
load ionosphere
tc = fitctree(X,Y)tc =
ClassificationTree
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'b' 'g'}
ScoreTransform: 'none'
NumObservations: 351
Properties, Methods
You can control the depth of the trees using the MaxNumSplits, MinLeafSize, or MinParentSize name-value pair parameters. fitctree grows deep decision trees by default. You can grow shallower trees to reduce model complexity or computation time.
Load the ionosphere data set.
load ionosphereThe default values of the tree depth controllers for growing classification trees are:
n - 1forMaxNumSplits.nis the training sample size.1forMinLeafSize.10forMinParentSize.
These default values tend to grow deep trees for large training sample sizes.
Train a classification tree using the default values for tree depth control. Cross-validate the model by using 10-fold cross-validation.
rng(1); % For reproducibility MdlDefault = fitctree(X,Y,'CrossVal','on');
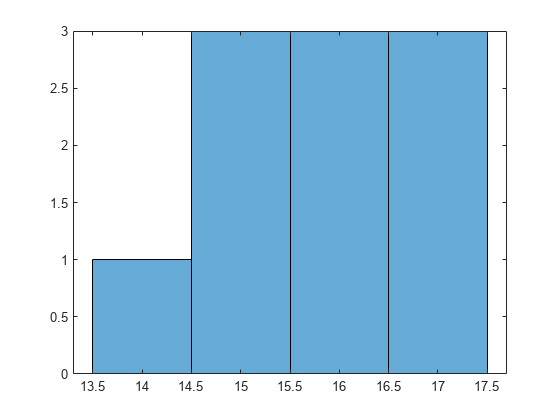
Draw a histogram of the number of imposed splits on the trees. Also, view one of the trees.
numBranches = @(x)sum(x.IsBranch); mdlDefaultNumSplits = cellfun(numBranches, MdlDefault.Trained); figure; histogram(mdlDefaultNumSplits)
view(MdlDefault.Trained{1},'Mode','graph')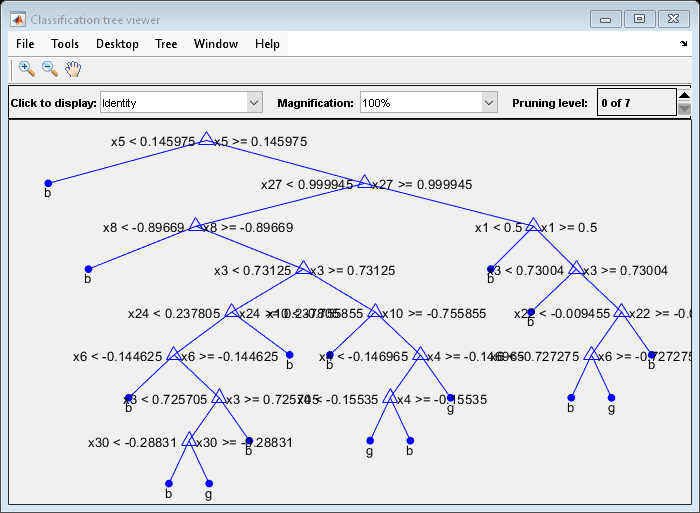
The average number of splits is around 15.
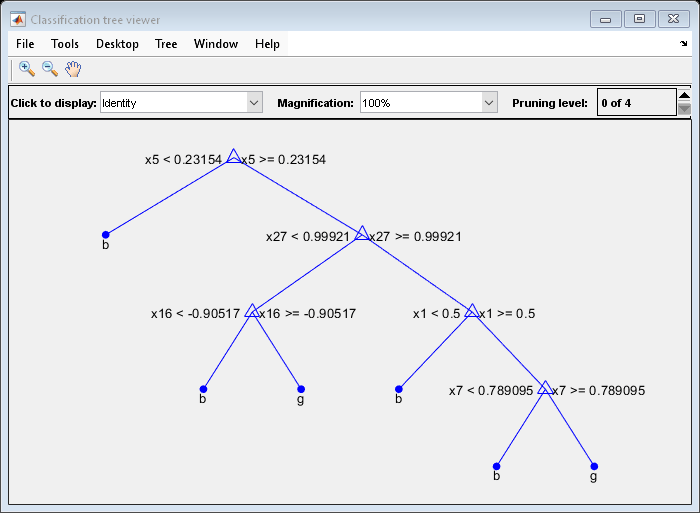
Suppose that you want a classification tree that is not as complex (deep) as the ones trained using the default number of splits. Train another classification tree, but set the maximum number of splits at 7, which is about half the mean number of splits from the default classification tree. Cross-validate the model by using 10-fold cross-validation.
Mdl7 = fitctree(X,Y,'MaxNumSplits',7,'CrossVal','on'); view(Mdl7.Trained{1},'Mode','graph')
Compare the cross-validation classification errors of the models.
classErrorDefault = kfoldLoss(MdlDefault)
classErrorDefault = 0.1168
classError7 = kfoldLoss(Mdl7)
classError7 = 0.1311
Mdl7 is much less complex and performs only slightly worse than MdlDefault.
More About
A decision tree splits nodes based on either impurity or node error.
Impurity means one of several things, depending on your choice of the
SplitCriterion name-value
argument:
Gini's Diversity Index (
gdi) — The Gini index of a node iswhere the sum is over the classes i at the node, and p(i) is the observed fraction of classes with class i that reach the node. A node with just one class (a pure node) has Gini index
0; otherwise, the Gini index is positive. So the Gini index is a measure of node impurity.Deviance (
"deviance") — With p(i) defined the same as for the Gini index, the deviance of a node isA pure node has deviance
0; otherwise, the deviance is positive.Twoing rule (
"twoing") — Twoing is not a purity measure of a node, but is a different measure for deciding how to split a node. Let L(i) denote the fraction of members of class i in the left child node after a split, and R(i) denote the fraction of members of class i in the right child node after a split. Choose the split criterion to maximizewhere P(L) and P(R) are the fractions of observations that split to the left and right, respectively. If the expression is large, the split made each child node purer. Similarly, if the expression is small, the split made each child node similar to each other and, therefore, similar to the parent node. The split did not increase node purity.
Node error — The node error is the fraction of misclassified classes at a node. If j is the class with the largest number of training samples at a node, the node error is
1 – p(j).
References
[1] Breiman, L., J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Boca Raton, FL: CRC Press, 1984.
Extended Capabilities
Usage notes and limitations:
To integrate the prediction of a classification tree model into Simulink®, you can use the ClassificationTree Predict block in the Statistics and Machine Learning Toolbox™ library or a MATLAB® Function block with the
predictfunction.When you train a classification tree using
fitctree, the following restrictions apply.The value of the
'ScoreTransform'name-value pair argument cannot be an anonymous function. For fixed-point code generation, the'ScoreTransform'value cannot be'invlogit'.You cannot use surrogate splits; that is, the value of the
'Surrogate'name-value pair argument must be'off'.For fixed-point code generation and code generation with a coder configurer, the following additional restrictions apply.
Categorical predictors (
logical,categorical,char,string, orcell) are not supported. You cannot use theCategoricalPredictorsname-value argument. To include categorical predictors in a model, preprocess them by usingdummyvarbefore fitting the model.Class labels with the
categoricaldata type are not supported. Both the class label value in the training data (TblorY) and the value of theClassNamesname-value argument cannot be an array with thecategoricaldata type.
For more information, see Introduction to Code Generation.
Usage notes and limitations:
The following object functions fully support GPU arrays:
The following object functions offer limited support for GPU arrays:
The object functions execute on a GPU if at least one of the following applies:
The model was fitted with GPU arrays.
The predictor data that you pass to the object function is a GPU array.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2011a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)