Generating Quasi-Random Numbers
Quasi-Random Sequences
Quasi-random number generators (QRNGs) produce highly uniform samples of the unit hypercube. QRNGs minimize the discrepancy between the distribution of generated points and a distribution with equal proportions of points in each sub-cube of a uniform partition of the hypercube. As a result, QRNGs systematically fill the “holes” in any initial segment of the generated quasi-random sequence.
Unlike the pseudorandom sequences described in Common Pseudorandom Number Generation Methods, quasi-random sequences fail many statistical tests for randomness. Approximating true randomness, however, is not their goal. Quasi-random sequences seek to fill space uniformly, and to do so in such a way that initial segments approximate this behavior up to a specified density.
QRNG applications include:
Quasi-Monte Carlo (QMC) integration. Monte Carlo techniques are often used to evaluate difficult, multi-dimensional integrals without a closed-form solution. QMC uses quasi-random sequences to improve the convergence properties of these techniques.
Space-filling experimental designs. In many experimental settings, taking measurements at every factor setting is expensive or infeasible. Quasi-random sequences provide efficient, uniform sampling of the design space.
Global optimization. Optimization algorithms typically find a local optimum in the neighborhood of an initial value. By using a quasi-random sequence of initial values, searches for global optima uniformly sample the basins of attraction of all local minima.
Example: Using Scramble, Leap, and Skip
Imagine a simple 1-D sequence that produces the integers from 1 to 10. This is the basic
sequence and the first three points are [1,2,3]:
![]()
Now look at how Scramble, Skip, and
Leap work together:
Scramble— Scrambling shuffles the points in one of several different ways. In this example, assume a scramble turns the sequence into1,3,5,7,9,2,4,6,8,10. The first three points are now[1,3,5]:
Skip— ASkipvalue specifies the number of initial points to ignore. In this example, set theSkipvalue to 2. The sequence is now5,7,9,2,4,6,8,10and the first three points are[5,7,9]:
Leap— ALeapvalue specifies the number of points to ignore for each one you take. Continuing the example with theSkipset to 2, if you set theLeapto 1, the sequence uses every other point. In this example, the sequence is now5,9,4,8and the first three points are[5,9,4]:
Quasi-Random Point Sets
Statistics and Machine Learning Toolbox™ functions support these quasi-random sequences:
Halton sequences. Produced by the
haltonsetfunction. These sequences use different prime bases to form successively finer uniform partitions of the unit interval in each dimension.Sobol sequences. Produced by the
sobolsetfunction. These sequences use a base of 2 to form successively finer uniform partitions of the unit interval, and then reorder the coordinates in each dimension.Latin hypercube sequences. Produced by the
lhsdesignfunction. Though not quasi-random in the sense of minimizing discrepancy, these sequences nevertheless produce sparse uniform samples useful in experimental designs.
Quasi-random sequences are functions from the positive integers to the unit hypercube. To be
useful in application, an initial point set of a sequence must be generated. Point sets are
matrices of size n-by-d, where n is
the number of points and d is the dimension of the hypercube being
sampled. The functions haltonset and sobolset construct point sets with properties of a specified quasi-random
sequence. Initial segments of the point sets are generated by the net method of the haltonset and sobolset classes, but points can be generated and accessed more generally using
parenthesis indexing.
Because of the way in which quasi-random sequences are generated, they may contain undesirable
correlations, especially in their initial segments, and especially in higher dimensions. To
address this issue, quasi-random point sets often skip, leap over, or scramble values in a sequence. The haltonset and sobolset functions allow you to specify both a
Skip and a Leap property of a quasi-random sequence,
and the scramble method of the haltonset and sobolset classes allows you apply a variety of
scrambling techniques. Scrambling reduces correlations while also improving
uniformity.
Generate a Quasi-Random Point Set
This example shows how to use haltonset to construct a 2-D Halton quasi-random point set.
Create a haltonset object p, that skips the first 1000 values of the sequence and then retains every 101st point.
rng default % For reproducibility p = haltonset(2,'Skip',1e3,'Leap',1e2)
p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : none
The object p encapsulates properties of the specified quasi-random sequence. The point set is finite, with a length determined by the Skip and Leap properties and by limits on the size of point set indices.
Use scramble to apply reverse-radix scrambling.
p = scramble(p,'RR2')p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : RR2
Use net to generate the first 500 points.
X0 = net(p,500);
This is equivalent to
X0 = p(1:500,:);
Values of the point set X0 are not generated and stored in memory until you access p using net or parenthesis indexing.
To appreciate the nature of quasi-random numbers, create a scatter plot of the two dimensions in X0.
scatter(X0(:,1),X0(:,2),5,'r') axis square title('{\bf Quasi-Random Scatter}')
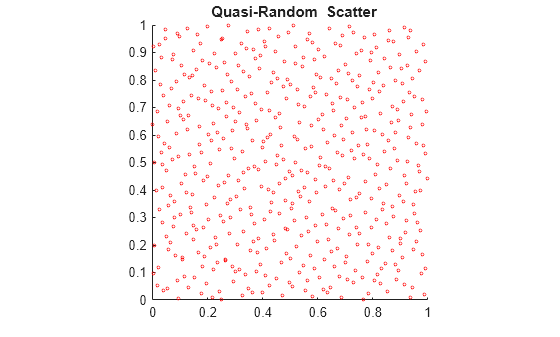
Compare this to a scatter of uniform pseudorandom numbers generated by the rand function.
X = rand(500,2); scatter(X(:,1),X(:,2),5,'b') axis square title('{\bf Uniform Random Scatter}')

The quasi-random scatter appears more uniform, avoiding the clumping in the pseudorandom scatter.
In a statistical sense, quasi-random numbers are too uniform to pass traditional tests of randomness. For example, a Kolmogorov-Smirnov test, performed by kstest, is used to assess whether or not a point set has a uniform random distribution. When performed repeatedly on uniform pseudorandom samples, such as those generated by rand, the test produces a uniform distribution of p-values.
nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = rand(sampSize,1); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end histogram(PVALS,100) h = findobj(gca,'Type','patch'); xlabel('{\it p}-values') ylabel('Number of Tests')

The results are quite different when the test is performed repeatedly on uniform quasi-random samples.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end histogram(PVALS,100) xlabel('{\it p}-values') ylabel('Number of Tests')

Small p-values call into question the null hypothesis that the data are uniformly distributed. If the hypothesis is true, about 5% of the p-values are expected to fall below 0.05. The results are remarkably consistent in their failure to challenge the hypothesis.
Quasi-Random Streams
Quasi-random streams, produced by the qrandstream function, are used to generate sequential quasi-random outputs,
rather than point sets of a specific size. Streams are used like pseudorandom number
generators, such as rand, when client applications require a
source of quasi-random numbers of indefinite size that can be accessed intermittently.
Properties of a quasi-random stream, such as its type (Halton or Sobol), dimension, skip,
leap, and scramble, are set when the stream is constructed.
In implementation, quasi-random streams are essentially very large quasi-random point sets,
though they are accessed differently. The state of a quasi-random stream is the scalar index of the
next point to be taken from the stream. Use the qrand method of the qrandstream
class to generate points from the stream, starting from the current state. Use the reset method to reset the state to 1. Unlike point sets,
streams do not support parenthesis indexing.
Generate a Quasi-Random Stream
This example shows how to generate samples from a quasi-random point set.
Use haltonset to create a quasi-random point set p, then repeatedly increment the index into the point set test to generate different samples.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end
The same results are obtained by using qrandstream to construct a quasi-random stream q based on the point set p and letting the stream take care of increments to the index.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); q = qrandstream(p); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests X = qrand(q,sampSize); [h,pval] = kstest(X,[X,X]); PVALS(test) = pval; end