Improve an Engine Cooling Fan Using Design for Six Sigma Techniques
This example shows how to improve the performance of an engine cooling fan through a Design for Six Sigma approach using Define, Measure, Analyze, Improve, and Control (DMAIC). The initial fan does not circulate enough air through the radiator to keep the engine cool during difficult conditions. First the example shows how to design an experiment to investigate the effect of three performance factors: fan distance from the radiator, blade-tip clearance, and blade pitch angle. It then shows how to estimate optimum values for each factor, resulting in a design that produces airflows beyond the goal of 875 ft per minute using test data. Finally it shows how to use simulations to verify that the new design produces airflow according to the specifications in more than 99.999% of the fans manufactured.
Define the Problem
This example addresses an engine cooling fan design that is unable to pull enough air through the radiator to keep the engine cool during difficult conditions, such as stop-and-go traffic or hot weather. Suppose you estimate that you need airflow of at least 875 ft/min to keep the engine cool during difficult conditions. You need to evaluate the current design and develop an alternative design that can achieve the target airflow.
Assess Cooling Fan Performance
Load the sample data, which is available when you run this example.
load("OriginalFan.mat")The data consists of 10,000 measurements (historical production data) of the existing cooling fan performance.
Plot the data to analyze the current fan's performance.
plot(originalfan) xlabel("Observation") ylabel("Max Airflow (ft^3/min)") title("Historical Production Data")
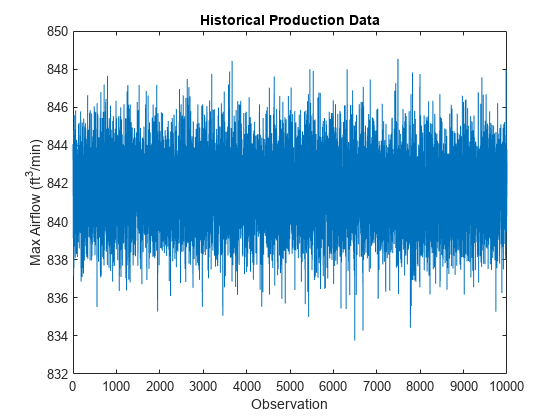
The data is centered around 842 ft/min and most values fall within the range of about 8 ft/min. The plot does not tell much about the underlying distribution of data, however. Plot the histogram and fit a normal distribution to the data.
figure histfit(originalfan) % Plot histogram with normal distribution fit format shortg xlabel("Airflow (ft^3/min)") ylabel("Frequency (counts)") title("Airflow Histogram")
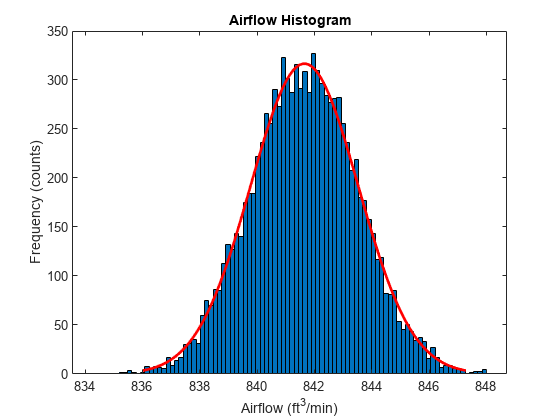
pd = fitdist(originalfan,"normal") % Fit normal distribution to data
pd =
NormalDistribution
Normal distribution
mu = 841.652 [841.616, 841.689]
sigma = 1.8768 [1.85114, 1.90318]
fitdist fits a normal distribution to data and estimates the parameters from data. The estimate for the mean airflow speed is 841.652 ft/min, and the 95% confidence interval for the mean airflow speed is (841.616, 841.689). This estimate makes it clear that the current fan is not close to the required 875 ft/min. There is need to improve the fan design to achieve the target airflow.
Determine Factors That Affect Fan Performance
Evaluate the factors that affect cooling fan performance using design of experiments (DOE). The response is the cooling fan airflow rate (ft/min). Suppose that the factors that you can modify and control are:
Distance from radiator
Pitch angle
Blade tip clearance
In general, fluid systems have nonlinear behavior. Therefore, use a response surface design to estimate any nonlinear interactions among the factors. Generate the experimental runs for a Box-Behnken design in coded (normalized) variables [-1, 0, +1]; see Box-Behnken Designs.
CodedValue = bbdesign(3)
CodedValue = 15×3
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
⋮
The first column is for the distance from radiator, the second column is for the pitch angle, and the third column is for the blade tip clearance. Suppose you want to test the effects of the variables at the following minimum and maximum values.
Distance from radiator: 1 to 1.5 inches
Pitch angle: 15 to 35 degrees
Blade tip clearance: 1 to 2 inches
Randomize the order of the runs, convert the coded design values to real-world units, and perform the experiment in the order specified.
runorder = randperm(15); % Random permutation of the runs bounds = [1 1.5;15 35;1 2]; % Min and max values for each factor RealValue = zeros(size(CodedValue)); for i = 1:size(CodedValue,2) % Convert coded values to real-world units zmax = max(CodedValue(:,i)); zmin = min(CodedValue(:,i)); RealValue(:,i) = interp1([zmin zmax],bounds(i,:),CodedValue(:,i)); end
Suppose that at the end of the experiments, you collect the following response values in the variable TestResult.
TestResult = [837 864 829 856 880 879 872 874 834 833 860 859 874 876 875]';
Save the design values and the response in a table.
Expmt = table(runorder', CodedValue(:,1), CodedValue(:,2), CodedValue(:,3), ... TestResult,'VariableNames',{'RunNumber','D','P','C','Airflow'});
Display the design values and the response.
disp(Expmt)
RunNumber D P C Airflow
_________ __ __ __ _______
6 -1 -1 0 837
3 -1 1 0 864
11 1 -1 0 829
7 1 1 0 856
14 -1 0 -1 880
8 -1 0 1 879
5 1 0 -1 872
15 1 0 1 874
1 0 -1 -1 834
2 0 -1 1 833
4 0 1 -1 860
13 0 1 1 859
9 0 0 0 874
10 0 0 0 876
12 0 0 0 875
D stands for Distance, P stands for Pitch, and C stands for Clearance. Based on the experimental test results, the airflow rate is sensitive to the changing factors values. Also, four experimental runs meet or exceed the target airflow rate of 875 ft/min (runs 2, 4,12, and 14). However, it is not clear which, if any, of these runs is the optimal one. In addition, it is not obvious how robust the design is to variation in the factors. Create a model based on the current experimental data and use the model to estimate the optimal factor settings.
Improve the Cooling Fan Performance
The Box-Behnken design enables you to test for nonlinear (quadratic) effects. The form of the quadratic model is:
where AF is the airflow rate and is the coefficient for the term . Estimate the coefficients of this model using the fitlm function.
mdl = fitlm(Expmt,"Airflow~D*P*C-D:P:C+D^2+P^2+C^2");Display the magnitudes of the coefficients (for normalized values) in a bar chart.
figure h = bar(mdl.Coefficients.Estimate(2:10)); set(h,"facecolor",[0.8 0.8 0.9]) legend("Coefficient") set(gcf,"units","normalized","position",[0.05 0.4 0.35 0.4]) set(gca,"xticklabel",mdl.CoefficientNames(2:10)) ylabel("Airflow (ft^3/min)") xlabel("Normalized Coefficient") title("Quadratic Model Coefficients")
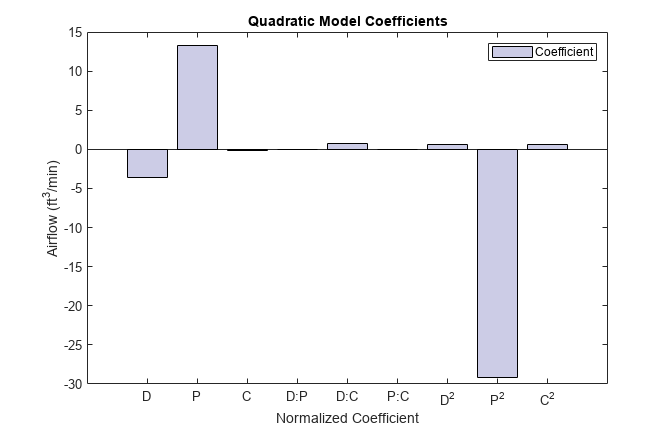
The bar chart shows that Pitch and Pitch are dominant factors. You can look at the relationship between multiple input variables and one output variable by generating a response surface plot. Use plotSlice to generate response surface plots for the model mdl interactively.
plotSlice(mdl)
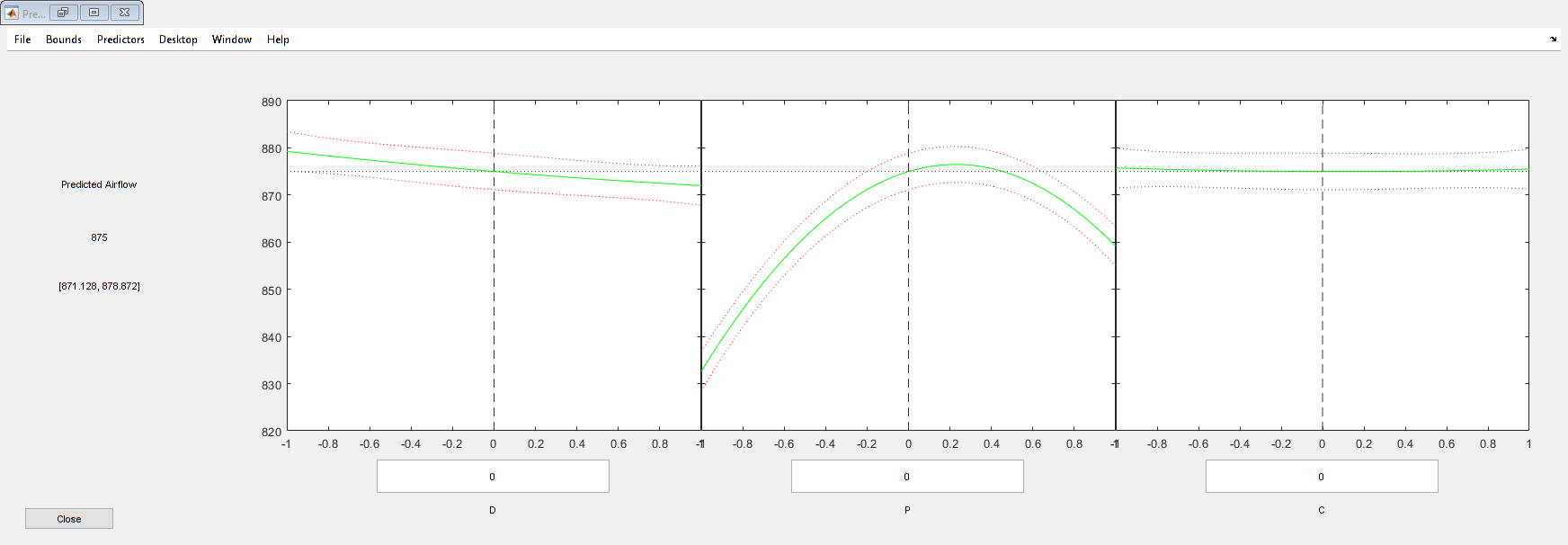
The plot shows the nonlinear relationship of airflow with pitch. Move the blue dashed lines around and see the effect the different factors have on airflow. Although you can use plotSlice to determine the optimum factor settings, you can also use Optimization Toolbox™ to automate the task.
Optimize Factor Settings
Find the optimal factor settings using the Problem-Based Optimization Workflow (Optimization Toolbox). First, define an optimization problem for maximization.
prob = optimproblem("ObjectiveSense","max");
Write the objective function using the x2fx function to convert the predictor matrix to a design matrix. Multiply the result by the model coefficient estimates.
fun = @(x) x2fx(x,"quadratic")*mdl.Coefficients.Estimate;Create an optimization variable named factors that is bounded between –1 and 1, and has three components, which represent the three factors.
factors = optimvar("factors",1,3,LowerBound=-1,UpperBound=1);Convert the objective function to an optimization expression in factors by using the fcn2optimexpr (Optimization Toolbox) function.
objective = fcn2optimexpr(fun,factors);
Place the objective function expression into the problem prob.
prob.Objective = objective;
Set the initial point to be the center of the design of the experimental test matrix, meaning the vector [0 0 0]. For the problem-based approach, the initial point must be a structure with the variable name as the name field.
x0 = struct("factors",[0 0 0]);Find the optimal design.
[sol,fval] = solve(prob,x0);
Solving problem using fmincon. Feasible point with lower objective function value found. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
Convert the results to real-world units.
maxloc = (sol.factors + 1)'; maxloc = bounds(:,1)+maxloc .* ((bounds(:,2) - bounds(:,1))/2); fprintf("Optimal Values:\n" + ... "Distance Pitch Clearance Airflow\n" + ... " %g %g %g %g\n",maxloc',fval);
Optimal Values: Distance Pitch Clearance Airflow 1 27.2747 1 882.257
The optimization result suggests placing the new fan one inch from the radiator, with pitch angle 27.3, and with a one-inch clearance between the tips of the fan blades and the shroud.
Because pitch angle has such a significant effect on airflow, perform additional analysis to verify that a 27.3 degree pitch angle is optimal.
load("AirflowData.mat") tbl = table(pitch,airflow); mdl2 = fitlm(tbl,"airflow~pitch^2"); mdl2.Rsquared.Ordinary
ans =
0.99632
The results show that a quadratic model explains the effect of pitch on the airflow well.
Plot the pitch angle against airflow and impose the fitted model.
figure plot(pitch,airflow,".r") hold on ylim([840 885]) line(pitch,mdl2.Fitted,"color","b") title("Fitted Model and Data") xlabel("Pitch angle (degrees)") ylabel("Airflow (ft^3/min)") legend("Test data","Quadratic model","Location","se") hold off
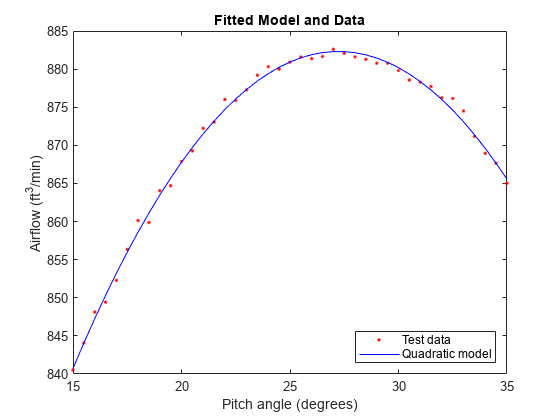
Find the pitch value that corresponds to the maximum airflow.
pitch(find(airflow==max(airflow)))
ans =
27
The additional analysis confirms that a 27.3 degree pitch angle is optimal.
The improved cooling fan design meets the airflow requirements. You also have a model that approximates the fan performance well based on the factors you can modify in the design. Ensure that the fan performance is robust to variability in manufacturing and installation by performing a sensitivity analysis.
Sensitivity Analysis
Suppose that, based on historical experience, the manufacturing uncertainty is as follows.
table(["Distance from radiator";"Blade pitch angle";"Blade tip clearance"],... ["1.00 +/- 0.05 inch";"27.3 +/- 0.25 degrees";"1.00 +/- 0.125 inch"],... ["1.00 +/- 0.20 inch";"0.227 +/- 0.028 degrees";"-1.00 +/- 0.25 inch"],... 'VariableNames',{'Factor' 'Real Values' 'Coded Values'})
ans=3×3 table
Factor Real Values Coded Values
________________________ _______________________ _________________________
"Distance from radiator" "1.00 +/- 0.05 inch" "1.00 +/- 0.20 inch"
"Blade pitch angle" "27.3 +/- 0.25 degrees" "0.227 +/- 0.028 degrees"
"Blade tip clearance" "1.00 +/- 0.125 inch" "-1.00 +/- 0.25 inch"
Verify that these variations in factors will enable to maintain a robust design around the target airflow. The philosophy of Six Sigma targets a defect rate of no more than 3.4 per 1,000,000 fans. That is, the fans must hit the 875 ft/min target 99.999% of the time.
You can verify the design using Monte Carlo simulation. Generate 10,000 random numbers for three factors with the specified tolerance. Include a noise variable that is proportional to the noise in the fitted model, mdl (that is, the RMS error of the model). Because the model coefficients are in coded variables, you must generate dist, pitch, and clearance using the coded definition.
dist = random("normal",sol.factors(1),0.20,[10000 1]); pitch = random("normal",sol.factors(2),0.028,[10000 1]); clearance = random("normal",sol.factors(3),0.25,[10000 1]); noise = random("normal",0,mdl2.RMSE,[10000 1]);
Calculate airflow for 10,000 random factor combinations using the model.
simfactor = [dist pitch clearance];
X = x2fx(simfactor,"quadratic");Add noise to the model (the variation in the data that the model did not account for).
simflow = X*mdl.Coefficients.Estimate+noise;
Evaluate the variation in the model's predicted airflow using a histogram. To estimate the mean and standard deviation, fit a normal distribution to data.
pd = fitdist(simflow,"normal"); figure histfit(simflow) hold on text(pd.mu+2,300,["Mean: " num2str(round(pd.mu))]) text(pd.mu+2,280,["Standard deviation: " num2str(round(pd.sigma))]) hold off xlabel("Airflow (ft^3/min)") ylabel("Frequency") title("Monte Carlo Simulation Results") hold off
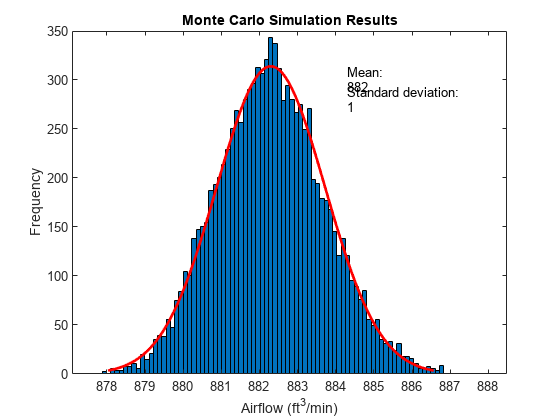
The results look promising. The average airflow is 882 ft/min and appears to be better than 875 ft/min for most of the data.
Determine the probability that the airflow is at 875 ft/min or below.
format long
pfail = cdf(pd,875)pfail =
1.454076873131737e-07
pass = (1-pfail)*100
pass = 99.999985459231269
The design appears to achieve at least 875 ft/min of airflow 99.999% of the time.
Use the simulation results to estimate the process capability.
S = capability(simflow,[875.0 890])
S = struct with fields:
mu: 8.822983078353724e+02
sigma: 1.422865134786495
P: 0.999999823569868
Pl: 1.454076873131737e-07
Pu: 3.102244433021162e-08
Cp: 1.757018243598422
Cpl: 1.709768001886212
Cpu: 1.804268485310632
Cpk: 1.709768001886212
pass = (1-S.Pl)*100
pass = 99.999985459231269
The Cp value is 1.75. A process is considered high quality when Cp is greater than or equal to 1.6. The Cpk is similar to the Cp value, which indicates that the process is centered. Now implement this design. Monitor to verify the design process and to ensure that the cooling fan delivers high-quality performance.
Control Manufacturing of the Improved Cooling Fan
You can monitor and evaluate the manufacturing and installation process of the new fan using control charts. Evaluate the first 30 days of production of the new cooling fan. Initially, five cooling fans per day were produced. First, load the sample data from the new process.
load("spcdata.mat")Plot the X-bar and S charts.
figure controlchart(spcflow,"chart",{'xbar','s'}) % Reshape the data into daily sets xlabel("Day")
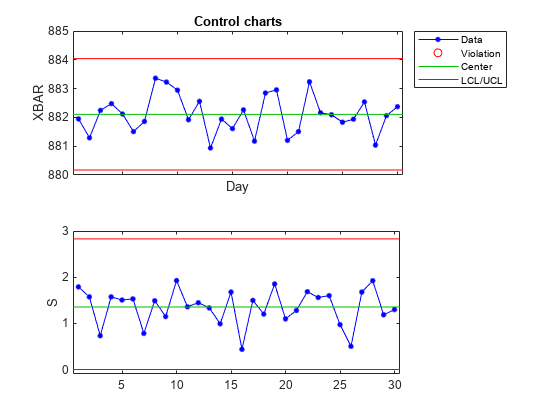
According to the results, the manufacturing process is in statistical control, as indicated by the absence of violations of control limits or nonrandom patterns in the data over time. You can also run a capability analysis on the data to evaluate the process.
[row,col] = size(spcflow); S2 = capability(reshape(spcflow,row*col,1),[875.0 890])
S2 = struct with fields:
mu: 8.821061141685465e+02
sigma: 1.423887508874697
P: 0.999999684316149
Pl: 3.008932155898586e-07
Pu: 1.479063578225176e-08
Cp: 1.755756676295137
Cpl: 1.663547652525458
Cpu: 1.847965700064817
Cpk: 1.663547652525458
pass = (1-S.Pl)*100
pass = 99.999985459231269
The Cp value of 1.755 is very similar to the estimated value of 1.73. The Cpk value of 1.66 is smaller than the Cp value. However, only a Cpk value less than 1.33, which indicates that the process shifted significantly toward one of the process limits, is a concern. The process is well within the limits and it achieves the target airflow (875 ft/min) more than 99.999% of the time.
See Also
bbdesign | fitlm | x2fx | solve (Optimization Toolbox) | controlchart | capability
Topics
- Box-Behnken Designs
- Problem-Based Optimization Workflow (Optimization Toolbox)