Select Predictors for Random Forests
This example shows how to choose the appropriate split predictor selection technique for your data set when growing a random forest of regression trees. This example also shows how to decide which predictors are most important to include in the training data.
Load and Preprocess Data
Load the carbig data set. Consider a model that predicts the fuel economy of a car given its number of cylinders, engine displacement, horsepower, weight, acceleration, model year, and country of origin. Consider Cylinders, Model_Year, and Origin as categorical variables.
load carbig
Cylinders = categorical(Cylinders);
Model_Year = categorical(Model_Year);
Origin = categorical(cellstr(Origin));
X = table(Cylinders,Displacement,Horsepower,Weight,Acceleration,Model_Year,Origin);Determine Levels in Predictors
The standard CART algorithm tends to split predictors with many unique values (levels), e.g., continuous variables, over those with fewer levels, e.g., categorical variables. If your data is heterogeneous, or your predictor variables vary greatly in their number of levels, then consider using the curvature or interaction tests for split-predictor selection instead of standard CART.
For each predictor, determine the number of levels in the data. One way to do this is define an anonymous function that:
Converts all variables to the categorical data type using
categoricalDetermines all unique categories while ignoring missing values using
categoriesCounts the categories using
numel
Then, apply the function to each variable using varfun.
countLevels = @(x)numel(categories(categorical(x))); numLevels = varfun(countLevels,X,'OutputFormat','uniform');
Compare the number of levels among the predictor variables.
figure bar(numLevels) title('Number of Levels Among Predictors') xlabel('Predictor variable') ylabel('Number of levels') h = gca; h.XTickLabel = X.Properties.VariableNames(1:end-1); h.XTickLabelRotation = 45; h.TickLabelInterpreter = 'none';
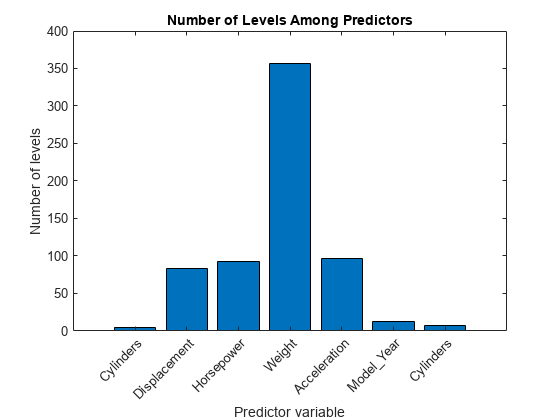
The continuous variables have many more levels than the categorical variables. Because the number of levels among the predictors varies so much, using standard CART to select split predictors at each node of the trees in a random forest can yield inaccurate predictor importance estimates. In this case, use the curvature test or interaction test. Specify the algorithm by using the 'PredictorSelection' name-value pair argument. For more details, see Choose Split Predictor Selection Technique.
Train Bagged Ensemble of Regression Trees
Train a bagged ensemble of 200 regression trees to estimate predictor importance values. Define a tree learner using these name-value pair arguments:
'NumVariablesToSample','all'— Use all predictor variables at each node to ensure that each tree uses all predictor variables.'PredictorSelection','interaction-curvature'— Specify usage of the interaction test to select split predictors.'Surrogate','on'— Specify usage of surrogate splits to increase accuracy because the data set includes missing values.
t = templateTree('NumVariablesToSample','all',... 'PredictorSelection','interaction-curvature','Surrogate','on'); rng(1); % For reproducibility Mdl = fitrensemble(X,MPG,'Method','Bag','NumLearningCycles',200, ... 'Learners',t);
Mdl is a RegressionBaggedEnsemble model.
Estimate the model using out-of-bag predictions.
yHat = oobPredict(Mdl); R2 = corr(Mdl.Y,yHat)^2
R2 = 0.8744
Mdl explains 87% of the variability around the mean.
Predictor Importance Estimation
Estimate predictor importance values by permuting out-of-bag observations among the trees.
impOOB = oobPermutedPredictorImportance(Mdl);
impOOB is a 1-by-7 vector of predictor importance estimates corresponding to the predictors in Mdl.PredictorNames. The estimates are not biased toward predictors containing many levels.
Compare the predictor importance estimates.
figure bar(impOOB) title('Unbiased Predictor Importance Estimates') xlabel('Predictor variable') ylabel('Importance') h = gca; h.XTickLabel = Mdl.PredictorNames; h.XTickLabelRotation = 45; h.TickLabelInterpreter = 'none';
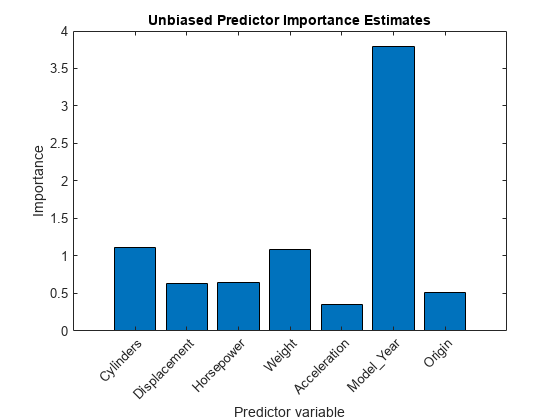
Greater importance estimates indicate more important predictors. The bar graph suggests that Model_Year is the most important predictor, followed by Cylinders and Weight. The Model_Year and Cylinders variables have only 13 and 5 distinct levels, respectively, whereas the Weight variable has over 300 levels.
Compare predictor importance estimates by permuting out-of-bag observations and those estimates obtained by summing gains in the mean squared error due to splits on each predictor. Also, obtain predictor association measures estimated by surrogate splits.
[impGain,predAssociation] = predictorImportance(Mdl); figure plot(1:numel(Mdl.PredictorNames),[impOOB' impGain']) title('Predictor Importance Estimation Comparison') xlabel('Predictor variable') ylabel('Importance') h = gca; h.XTickLabel = Mdl.PredictorNames; h.XTickLabelRotation = 45; h.TickLabelInterpreter = 'none'; legend('OOB permuted','MSE improvement') grid on
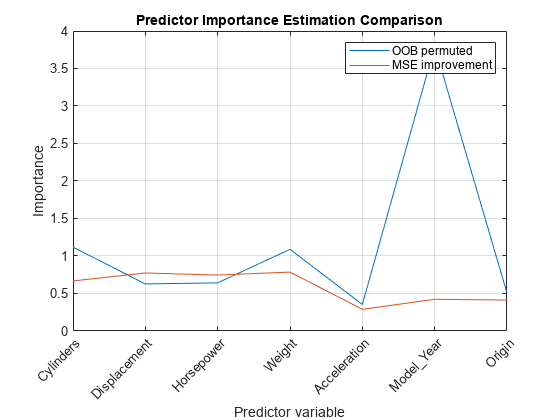
According to the values of impGain, the variables Displacement, Horsepower, and Weight appear to be equally important.
predAssociation is a 7-by-7 matrix of predictor association measures. Rows and columns correspond to the predictors in Mdl.PredictorNames. The Predictive Measure of Association is a value that indicates the similarity between decision rules that split observations. The best surrogate decision split yields the maximum predictive measure of association. You can infer the strength of the relationship between pairs of predictors using the elements of predAssociation. Larger values indicate more highly correlated pairs of predictors.
figure imagesc(predAssociation) title('Predictor Association Estimates') colorbar h = gca; h.XTickLabel = Mdl.PredictorNames; h.XTickLabelRotation = 45; h.TickLabelInterpreter = 'none'; h.YTickLabel = Mdl.PredictorNames;
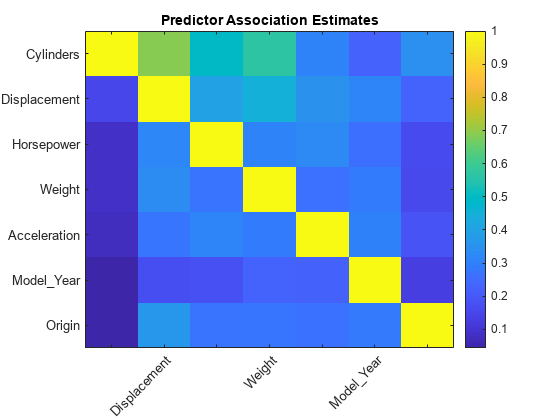
predAssociation(1,2)
ans = 0.6871
The largest association is between Cylinders and Displacement, but the value is not high enough to indicate a strong relationship between the two predictors.
Grow Random Forest Using Reduced Predictor Set
Because prediction time increases with the number of predictors in random forests, a good practice is to create a model using as few predictors as possible.
Grow a random forest of 200 regression trees using the best two predictors only. The default 'NumVariablesToSample' value of templateTree is one third of the number of predictors for regression, so fitrensemble uses the random forest algorithm.
t = templateTree('PredictorSelection','interaction-curvature','Surrogate','on', ... 'Reproducible',true); % For reproducibility of random predictor selections MdlReduced = fitrensemble(X(:,{'Model_Year' 'Weight'}),MPG,'Method','Bag', ... 'NumLearningCycles',200,'Learners',t);
Compute the of the reduced model.
yHatReduced = oobPredict(MdlReduced); r2Reduced = corr(Mdl.Y,yHatReduced)^2
r2Reduced = 0.8653
The for the reduced model is close to the of the full model. This result suggests that the reduced model is sufficient for prediction.
See Also
templateTree | fitrensemble | oobPredict | oobPermutedPredictorImportance | predictorImportance | corr