fitrensemble
Fit ensemble of learners for regression
Syntax
Description
Mdl = fitrensemble(Tbl,ResponseVarName)Mdl. By
default, Mdl contains the results of boosting 100
regression trees using LSBoost and the predictor and response data in the table
Tbl. ResponseVarName is the name of
the response variable in Tbl.
Mdl = fitrensemble(Tbl,formula)formula to fit the model to the predictor and
response data in the table Tbl. formula is
an explanatory model of the response and a subset of predictor variables in
Tbl used to fit Mdl. For example,
'Y~X1+X2+X3' fits the response variable
Tbl.Y as a function of the predictor variables
Tbl.X1, Tbl.X2, and
Tbl.X3.
Mdl = fitrensemble(___,Name,Value)Name,Value
pair arguments and any of the input arguments in the previous syntaxes. For
example, you can specify the number of learning cycles, the ensemble aggregation
method, or to implement 10-fold cross-validation.
[
also returns Mdl,AggregateOptimizationResults] = fitrensemble(___)AggregateOptimizationResults, which contains
hyperparameter optimization results when you specify the
OptimizeHyperparameters and
HyperparameterOptimizationOptions name-value arguments.
You must also specify the ConstraintType and
ConstraintBounds options of
HyperparameterOptimizationOptions. You can use this
syntax to optimize on compact model size instead of cross-validation loss, and
to perform a set of multiple optimization problems that have the same options
but different constraint bounds.
Examples
Create a regression ensemble that predicts the fuel economy of a car given the number of cylinders, volume displaced by the cylinders, horsepower, and weight. Then, train another ensemble using fewer predictors. Compare the in-sample predictive accuracies of the ensembles.
Load the carsmall data set. Store the variables to be used in training in a table.
load carsmall
Tbl = table(Cylinders,Displacement,Horsepower,Weight,MPG);Train a regression ensemble.
Mdl1 = fitrensemble(Tbl,'MPG');Mdl1 is a RegressionEnsemble model. Some notable characteristics of Mdl1 are:
The ensemble aggregation algorithm is
'LSBoost'.Because the ensemble aggregation method is a boosting algorithm, regression trees that allow a maximum of 10 splits compose the ensemble.
One hundred trees compose the ensemble.
Because MPG is a variable in the MATLAB® Workspace, you can obtain the same result by entering
Mdl1 = fitrensemble(Tbl,MPG);
Use the trained regression ensemble to predict the fuel economy for a four-cylinder car with a 200-cubic inch displacement, 150 horsepower, and weighing 3000 lbs.
pMPG = predict(Mdl1,[4 200 150 3000])
pMPG = 25.6467
Train a new ensemble using all predictors in Tbl except Displacement.
formula = 'MPG ~ Cylinders + Horsepower + Weight';
Mdl2 = fitrensemble(Tbl,formula);Compare the resubstitution MSEs between Mdl1 and Mdl2.
mse1 = resubLoss(Mdl1)
mse1 = 0.3096
mse2 = resubLoss(Mdl2)
mse2 = 0.5861
The in-sample MSE for the ensemble that trains on all predictors is lower.
Train an ensemble of boosted regression trees by using fitrensemble. Reduce training time by specifying the 'NumBins' name-value pair argument to bin numeric predictors. After training, you can reproduce binned predictor data by using the BinEdges property of the trained model and the discretize function.
Generate a sample data set.
rng('default') % For reproducibility N = 1e6; X1 = randi([-1,5],[N,1]); X2 = randi([5,10],[N,1]); X3 = randi([0,5],[N,1]); X4 = randi([1,10],[N,1]); X = [X1 X2 X3 X4]; y = X1 + X2 + X3 + X4 + normrnd(0,1,[N,1]);
Train an ensemble of boosted regression trees using least-squares boosting (LSBoost, the default value). Time the function for comparison purposes.
tic Mdl1 = fitrensemble(X,y); toc
Elapsed time is 78.662954 seconds.
Speed up training by using the 'NumBins' name-value pair argument. If you specify the 'NumBins' value as a positive integer scalar, then the software bins every numeric predictor into a specified number of equiprobable bins, and then grows trees on the bin indices instead of the original data. The software does not bin categorical predictors.
tic
Mdl2 = fitrensemble(X,y,'NumBins',50);
tocElapsed time is 43.353208 seconds.
The process is about two times faster when you use binned data instead of the original data. Note that the elapsed time can vary depending on your operating system.
Compare the regression errors by resubstitution.
rsLoss = resubLoss(Mdl1)
rsLoss = 1.0134
rsLoss2 = resubLoss(Mdl2)
rsLoss2 = 1.0133
In this example, binning predictor values reduces training time without a significant loss of accuracy. In general, when you have a large data set like the one in this example, using the binning option speeds up training but causes a potential decrease in accuracy. If you want to reduce training time further, specify a smaller number of bins.
Reproduce binned predictor data by using the BinEdges property of the trained model and the discretize function.
X = Mdl2.X; % Predictor data Xbinned = zeros(size(X)); edges = Mdl2.BinEdges; % Find indices of binned predictors. idxNumeric = find(~cellfun(@isempty,edges)); if iscolumn(idxNumeric) idxNumeric = idxNumeric'; end for j = idxNumeric x = X(:,j); % Convert x to array if x is a table. if istable(x) x = table2array(x); end % Group x into bins by using the discretize function. xbinned = discretize(x,[-inf; edges{j}; inf]); Xbinned(:,j) = xbinned; end
Xbinned contains the bin indices, ranging from 1 to the number of bins, for numeric predictors. Xbinned values are 0 for categorical predictors. If X contains NaNs, then the corresponding Xbinned values are NaNs.
Estimate the generalization error of an ensemble of boosted regression trees.
Load the carsmall data set. Choose the number of cylinders, volume displaced by the cylinders, horsepower, and weight as predictors of fuel economy.
load carsmall
X = [Cylinders Displacement Horsepower Weight];Cross-validate an ensemble of regression trees using 10-fold cross-validation. Using a decision tree template, specify that each tree should be a split once only.
rng(1); % For reproducibility t = templateTree('MaxNumSplits',1); Mdl = fitrensemble(X,MPG,'Learners',t,'CrossVal','on');
Mdl is a RegressionPartitionedEnsemble model.
Plot the cumulative, 10-fold cross-validated, mean-squared error (MSE). Display the estimated generalization error of the ensemble.
kflc = kfoldLoss(Mdl,'Mode','cumulative'); figure; plot(kflc); ylabel('10-fold cross-validated MSE'); xlabel('Learning cycle');
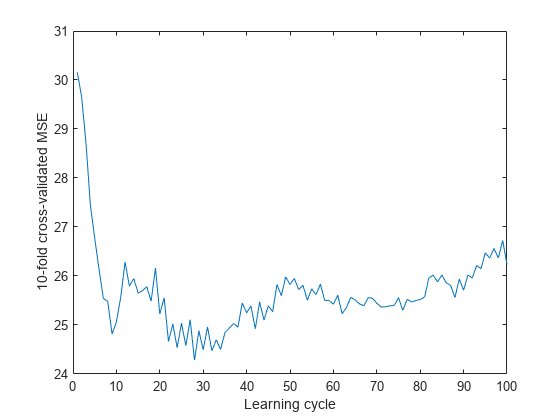
estGenError = kflc(end)
estGenError = 26.2356
kfoldLoss returns the generalization error by default. However, plotting the cumulative loss allows you to monitor how the loss changes as weak learners accumulate in the ensemble.
The ensemble achieves an MSE of around 23.5 after accumulating about 30 weak learners.
If you are satisfied with the generalization error of the ensemble, then, to create a predictive model, train the ensemble again using all of the settings except cross-validation. However, it is good practice to tune hyperparameters such as the maximum number of decision splits per tree and the number of learning cycles..
This example shows how to optimize hyperparameters automatically using fitrensemble. The example uses the carsmall data.
Load the data.
load carsmallYou can find hyperparameters that minimize five-fold cross-validation loss by using automatic hyperparameter optimization.
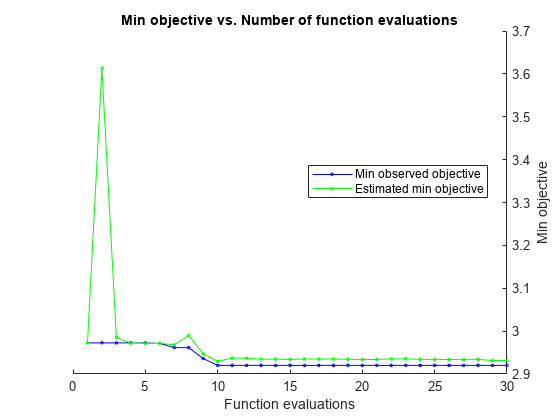
Mdl = fitrensemble([Horsepower,Weight],MPG,'OptimizeHyperparameters','auto')
In this example, for reproducibility, set the random seed and use the 'expected-improvement-plus' acquisition function. Also, for reproducibility of random forest algorithm, specify the 'Reproducible' name-value pair argument as true for tree learners.
rng('default') t = templateTree('Reproducible',true); Mdl = fitrensemble([Horsepower,Weight],MPG,'OptimizeHyperparameters','auto','Learners',t, ... 'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName','expected-improvement-plus'))
|===================================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Method | NumLearningC-| LearnRate | MinLeafSize |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | ycles | | |
|===================================================================================================================================|
| 1 | Best | 2.9726 | 5.3926 | 2.9726 | 2.9726 | Bag | 413 | - | 1 |
| 2 | Accept | 6.2619 | 1.2117 | 2.9726 | 3.6133 | LSBoost | 57 | 0.0016067 | 6 |
| 3 | Accept | 2.9975 | 0.42937 | 2.9726 | 2.9852 | Bag | 32 | - | 2 |
| 4 | Accept | 4.1897 | 0.62946 | 2.9726 | 2.972 | Bag | 55 | - | 40 |
| 5 | Accept | 6.3321 | 0.99489 | 2.9726 | 2.9715 | LSBoost | 55 | 0.001005 | 2 |
| 6 | Best | 2.9714 | 0.49119 | 2.9714 | 2.9715 | Bag | 39 | - | 1 |
| 7 | Best | 2.9615 | 0.66561 | 2.9615 | 2.9681 | Bag | 55 | - | 1 |
| 8 | Accept | 3.017 | 0.24581 | 2.9615 | 2.98 | Bag | 17 | - | 1 |
| 9 | Accept | 4.1881 | 2.937 | 2.9615 | 2.9801 | LSBoost | 164 | 0.93989 | 50 |
| 10 | Accept | 3.6972 | 0.34811 | 2.9615 | 2.98 | LSBoost | 12 | 0.99469 | 1 |
| 11 | Accept | 3.3742 | 0.57845 | 2.9615 | 2.9801 | LSBoost | 15 | 0.13227 | 1 |
| 12 | Accept | 4.1881 | 3.636 | 2.9615 | 2.9799 | LSBoost | 205 | 0.083595 | 48 |
| 13 | Accept | 5.0943 | 0.92811 | 2.9615 | 2.9799 | LSBoost | 48 | 0.014581 | 1 |
| 14 | Accept | 5.5926 | 0.90861 | 2.9615 | 2.9796 | LSBoost | 47 | 0.010771 | 50 |
| 15 | Accept | 6.39 | 0.53215 | 2.9615 | 2.9793 | LSBoost | 27 | 0.0010688 | 50 |
| 16 | Accept | 3.3304 | 1.4184 | 2.9615 | 2.9793 | LSBoost | 78 | 0.32479 | 7 |
| 17 | Accept | 4.6487 | 0.38207 | 2.9615 | 2.9795 | LSBoost | 17 | 0.055039 | 5 |
| 18 | Accept | 3.264 | 0.27432 | 2.9615 | 2.9796 | LSBoost | 11 | 0.29878 | 1 |
| 19 | Accept | 4.1904 | 0.29445 | 2.9615 | 2.9621 | LSBoost | 13 | 0.26663 | 50 |
| 20 | Accept | 3.5279 | 8.6465 | 2.9615 | 2.9626 | LSBoost | 499 | 0.25522 | 1 |
|===================================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Method | NumLearningC-| LearnRate | MinLeafSize |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | ycles | | |
|===================================================================================================================================|
| 21 | Best | 2.9162 | 4.6697 | 2.9162 | 2.9178 | Bag | 423 | - | 2 |
| 22 | Best | 2.9009 | 5.478 | 2.9009 | 2.9043 | Bag | 499 | - | 3 |
| 23 | Accept | 2.9064 | 5.6002 | 2.9009 | 2.9053 | Bag | 499 | - | 3 |
| 24 | Accept | 2.909 | 5.6418 | 2.9009 | 2.9065 | Bag | 494 | - | 3 |
| 25 | Accept | 2.9011 | 6.2361 | 2.9009 | 2.9051 | Bag | 499 | - | 3 |
| 26 | Accept | 3.1863 | 0.29822 | 2.9009 | 2.9048 | LSBoost | 10 | 0.99529 | 10 |
| 27 | Accept | 3.5444 | 9.3008 | 2.9009 | 2.9049 | LSBoost | 476 | 0.97599 | 5 |
| 28 | Accept | 3.2334 | 0.33247 | 2.9009 | 2.9048 | LSBoost | 12 | 0.55679 | 4 |
| 29 | Best | 2.8547 | 5.3697 | 2.8547 | 2.8575 | Bag | 487 | - | 5 |
| 30 | Best | 2.84 | 5.6298 | 2.84 | 2.8436 | Bag | 499 | - | 6 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 90.6421 seconds
Total objective function evaluation time: 79.5016
Best observed feasible point:
Method NumLearningCycles LearnRate MinLeafSize
______ _________________ _________ ___________
Bag 499 NaN 6
Observed objective function value = 2.84
Estimated objective function value = 2.8436
Function evaluation time = 5.6298
Best estimated feasible point (according to models):
Method NumLearningCycles LearnRate MinLeafSize
______ _________________ _________ ___________
Bag 499 NaN 6
Estimated objective function value = 2.8436
Estimated function evaluation time = 5.683
Mdl =
RegressionBaggedEnsemble
ResponseName: 'Y'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
NumTrained: 499
Method: 'Bag'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: []
FitInfoDescription: 'None'
Regularization: []
FResample: 1
Replace: 1
UseObsForLearner: [94×499 logical]
Properties, Methods
The optimization searched over the methods for regression (Bag and LSBoost), over NumLearningCycles, over the LearnRate for LSBoost, and over the tree learner MinLeafSize. The output is the ensemble regression with the minimum estimated cross-validation loss.
One way to create an ensemble of boosted regression trees that has satisfactory predictive performance is to tune the decision tree complexity level using cross-validation. While searching for an optimal complexity level, tune the learning rate to minimize the number of learning cycles as well.
This example manually finds optimal parameters by using the cross-validation option (the 'KFold' name-value pair argument) and the kfoldLoss function. Alternatively, you can use the 'OptimizeHyperparameters' name-value pair argument to optimize hyperparameters automatically. See Optimize Regression Ensemble.
Load the carsmall data set. Choose the number of cylinders, volume displaced by the cylinders, horsepower, and weight as predictors of fuel economy.
load carsmall
Tbl = table(Cylinders,Displacement,Horsepower,Weight,MPG);The default values of the tree depth controllers for boosting regression trees are:
10forMaxNumSplits.5forMinLeafSize10forMinParentSize
To search for the optimal tree-complexity level:
Cross-validate a set of ensembles. Exponentially increase the tree-complexity level for subsequent ensembles from decision stump (one split) to at most n - 1 splits. n is the sample size. Also, vary the learning rate for each ensemble between 0.1 to 1.
Estimate the cross-validated mean-squared error (MSE) for each ensemble.
For tree-complexity level , , compare the cumulative, cross-validated MSE of the ensembles by plotting them against number of learning cycles. Plot separate curves for each learning rate on the same figure.
Choose the curve that achieves the minimal MSE, and note the corresponding learning cycle and learning rate.
Cross-validate a deep regression tree and a stump. Because the data contain missing values, use surrogate splits. These regression trees serve as benchmarks.
rng(1) % For reproducibility MdlDeep = fitrtree(Tbl,'MPG','CrossVal','on','MergeLeaves','off', ... 'MinParentSize',1,'Surrogate','on'); MdlStump = fitrtree(Tbl,'MPG','MaxNumSplits',1,'CrossVal','on', ... 'Surrogate','on');
Cross-validate an ensemble of 150 boosted regression trees using 5-fold cross-validation. Using a tree template:
Vary the maximum number of splits using the values in the sequence . m is such that is no greater than n - 1.
Turn on surrogate splits.
For each variant, adjust the learning rate using each value in the set {0.1, 0.25, 0.5, 1}.
n = size(Tbl,1); m = floor(log2(n - 1)); learnRate = [0.1 0.25 0.5 1]; numLR = numel(learnRate); maxNumSplits = 2.^(0:m); numMNS = numel(maxNumSplits); numTrees = 150; Mdl = cell(numMNS,numLR); for k = 1:numLR for j = 1:numMNS t = templateTree('MaxNumSplits',maxNumSplits(j),'Surrogate','on'); Mdl{j,k} = fitrensemble(Tbl,'MPG','NumLearningCycles',numTrees, ... 'Learners',t,'KFold',5,'LearnRate',learnRate(k)); end end
Estimate the cumulative, cross-validated MSE of each ensemble.
kflAll = @(x)kfoldLoss(x,'Mode','cumulative'); errorCell = cellfun(kflAll,Mdl,'Uniform',false); error = reshape(cell2mat(errorCell),[numTrees numel(maxNumSplits) numel(learnRate)]); errorDeep = kfoldLoss(MdlDeep); errorStump = kfoldLoss(MdlStump);
Plot how the cross-validated MSE behaves as the number of trees in the ensemble increases. Plot the curves with respect to learning rate on the same plot, and plot separate plots for varying tree-complexity levels. Choose a subset of tree complexity levels to plot.
mnsPlot = [1 round(numel(maxNumSplits)/2) numel(maxNumSplits)]; figure; for k = 1:3 subplot(2,2,k) plot(squeeze(error(:,mnsPlot(k),:)),'LineWidth',2) axis tight hold on h = gca; plot(h.XLim,[errorDeep errorDeep],'-.b','LineWidth',2) plot(h.XLim,[errorStump errorStump],'-.r','LineWidth',2) plot(h.XLim,min(min(error(:,mnsPlot(k),:))).*[1 1],'--k') h.YLim = [10 50]; xlabel('Number of trees') ylabel('Cross-validated MSE') title(sprintf('MaxNumSplits = %0.3g', maxNumSplits(mnsPlot(k)))) hold off end hL = legend([cellstr(num2str(learnRate','Learning Rate = %0.2f')); ... 'Deep Tree';'Stump';'Min. MSE']); hL.Position(1) = 0.6;
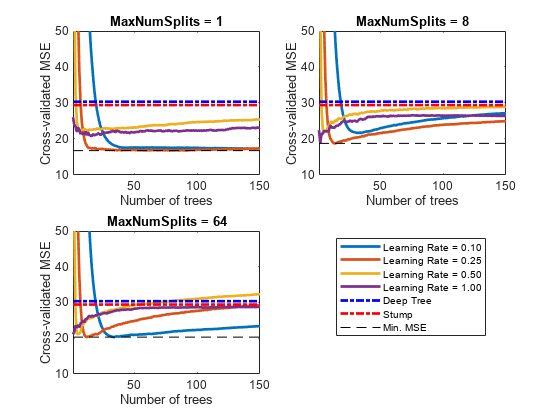
Each curve contains a minimum cross-validated MSE occurring at the optimal number of trees in the ensemble.
Identify the maximum number of splits, number of trees, and learning rate that yields the lowest MSE overall.
[minErr,minErrIdxLin] = min(error(:));
[idxNumTrees,idxMNS,idxLR] = ind2sub(size(error),minErrIdxLin);
fprintf('\nMin. MSE = %0.5f',minErr)Min. MSE = 16.77593
fprintf('\nOptimal Parameter Values:\nNum. Trees = %d',idxNumTrees);Optimal Parameter Values: Num. Trees = 78
fprintf('\nMaxNumSplits = %d\nLearning Rate = %0.2f\n',... maxNumSplits(idxMNS),learnRate(idxLR))
MaxNumSplits = 1 Learning Rate = 0.25
Create a predictive ensemble based on the optimal hyperparameters and the entire training set.
tFinal = templateTree('MaxNumSplits',maxNumSplits(idxMNS),'Surrogate','on'); MdlFinal = fitrensemble(Tbl,'MPG','NumLearningCycles',idxNumTrees, ... 'Learners',tFinal,'LearnRate',learnRate(idxLR))
MdlFinal =
RegressionEnsemble
PredictorNames: {'Cylinders' 'Displacement' 'Horsepower' 'Weight'}
ResponseName: 'MPG'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
NumTrained: 78
Method: 'LSBoost'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [78×1 double]
FitInfoDescription: {2×1 cell}
Regularization: []
Properties, Methods
MdlFinal is a RegressionEnsemble. To predict the fuel economy of a car given its number of cylinders, volume displaced by the cylinders, horsepower, and weight, you can pass the predictor data and MdlFinal to predict.
Instead of searching optimal values manually by using the cross-validation option ('KFold') and the kfoldLoss function, you can use the 'OptimizeHyperparameters' name-value pair argument. When you specify 'OptimizeHyperparameters', the software finds optimal parameters automatically using Bayesian optimization. The optimal values obtained by using 'OptimizeHyperparameters' can be different from those obtained using manual search.
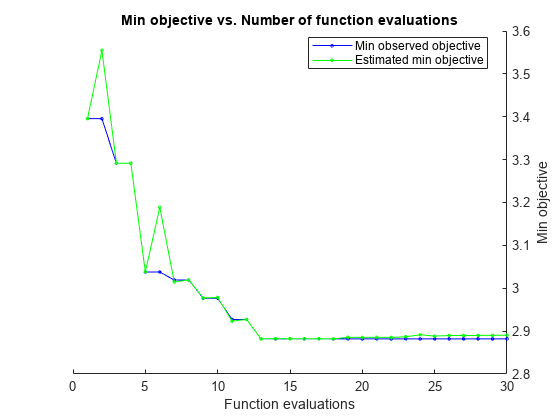
t = templateTree('Surrogate','on'); mdl = fitrensemble(Tbl,'MPG','Learners',t, ... 'OptimizeHyperparameters',{'NumLearningCycles','LearnRate','MaxNumSplits'})
|====================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | NumLearningC-| LearnRate | MaxNumSplits |
| | result | log(1+loss) | runtime | (observed) | (estim.) | ycles | | |
|====================================================================================================================|
| 1 | Best | 3.3955 | 0.94402 | 3.3955 | 3.3955 | 26 | 0.072054 | 3 |
| 2 | Accept | 6.0976 | 3.9117 | 3.3955 | 3.5549 | 170 | 0.0010295 | 70 |
| 3 | Best | 3.2914 | 6.0968 | 3.2914 | 3.2917 | 273 | 0.61026 | 6 |
| 4 | Accept | 6.1839 | 1.7989 | 3.2914 | 3.2915 | 80 | 0.0016871 | 1 |
| 5 | Best | 3.0273 | 0.57588 | 3.0273 | 3.0278 | 15 | 0.21599 | 10 |
| 6 | Accept | 3.3234 | 0.45074 | 3.0273 | 3.1684 | 10 | 0.18084 | 4 |
| 7 | Best | 2.9751 | 0.72605 | 2.9751 | 3.1054 | 10 | 0.26528 | 2 |
| 8 | Accept | 3.0367 | 0.87606 | 2.9751 | 3.0847 | 10 | 0.27397 | 32 |
| 9 | Best | 2.9587 | 0.85912 | 2.9587 | 2.9669 | 10 | 0.2779 | 6 |
| 10 | Accept | 3.0926 | 0.63378 | 2.9587 | 2.9681 | 13 | 0.96319 | 1 |
| 11 | Best | 2.9368 | 1.4893 | 2.9368 | 2.9372 | 28 | 0.40597 | 1 |
| 12 | Accept | 2.9838 | 0.88098 | 2.9368 | 2.9577 | 10 | 0.48395 | 2 |
| 13 | Accept | 3.1625 | 0.87138 | 2.9368 | 3.0327 | 17 | 0.42369 | 38 |
| 14 | Accept | 2.959 | 0.43069 | 2.9368 | 2.9387 | 10 | 0.4064 | 1 |
| 15 | Accept | 5.9673 | 0.3728 | 2.9368 | 2.9368 | 10 | 0.023931 | 88 |
| 16 | Best | 2.9188 | 9.3029 | 2.9188 | 2.919 | 475 | 0.19759 | 1 |
| 17 | Best | 2.9151 | 5.0215 | 2.9151 | 2.9014 | 280 | 0.27661 | 1 |
| 18 | Accept | 3.0182 | 0.34635 | 2.9151 | 2.9145 | 10 | 0.70662 | 1 |
| 19 | Accept | 3.1713 | 4.4133 | 2.9151 | 2.8988 | 207 | 0.11131 | 98 |
| 20 | Accept | 2.9327 | 0.70644 | 2.9151 | 2.9141 | 18 | 0.301 | 1 |
|====================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | NumLearningC-| LearnRate | MaxNumSplits |
| | result | log(1+loss) | runtime | (observed) | (estim.) | ycles | | |
|====================================================================================================================|
| 21 | Accept | 3.2178 | 2.8981 | 2.9151 | 2.9192 | 133 | 0.23864 | 20 |
| 22 | Best | 2.9118 | 0.35284 | 2.9118 | 2.9079 | 10 | 0.32758 | 1 |
| 23 | Accept | 6.3194 | 0.27751 | 2.9118 | 2.9079 | 10 | 0.0061881 | 91 |
| 24 | Accept | 6.3858 | 0.30949 | 2.9118 | 2.9088 | 10 | 0.0028347 | 98 |
| 25 | Accept | 6.4221 | 0.29272 | 2.9118 | 2.9088 | 10 | 0.0010219 | 1 |
| 26 | Accept | 6.2046 | 0.28315 | 2.9118 | 2.9094 | 10 | 0.012343 | 1 |
| 27 | Accept | 5.6755 | 0.34641 | 2.9118 | 2.9173 | 10 | 0.039622 | 1 |
| 28 | Accept | 3.4559 | 0.38746 | 2.9118 | 2.9064 | 10 | 0.99683 | 98 |
| 29 | Accept | 2.9564 | 0.37626 | 2.9118 | 2.9316 | 10 | 0.31556 | 1 |
| 30 | Accept | 2.9309 | 0.94302 | 2.9118 | 2.9309 | 45 | 0.13675 | 1 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 72.9074 seconds
Total objective function evaluation time: 47.1757
Best observed feasible point:
NumLearningCycles LearnRate MaxNumSplits
_________________ _________ ____________
10 0.32758 1
Observed objective function value = 2.9118
Estimated objective function value = 2.9309
Function evaluation time = 0.35284
Best estimated feasible point (according to models):
NumLearningCycles LearnRate MaxNumSplits
_________________ _________ ____________
10 0.32758 1
Estimated objective function value = 2.9309
Estimated function evaluation time = 0.44588
mdl =
RegressionEnsemble
PredictorNames: {'Cylinders' 'Displacement' 'Horsepower' 'Weight'}
ResponseName: 'MPG'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
NumTrained: 10
Method: 'LSBoost'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [10×1 double]
FitInfoDescription: {2×1 cell}
Regularization: []
Properties, Methods
Input Arguments
Sample data used to train the model, specified as a table. Each
row of Tbl corresponds to one observation, and
each column corresponds to one predictor variable. Tbl can
contain one additional column for the response variable. Multicolumn
variables and cell arrays other than cell arrays of character vectors
are not allowed.
If
Tblcontains the response variable and you want to use all remaining variables as predictors, then specify the response variable usingResponseVarName.If
Tblcontains the response variable, and you want to use a subset of the remaining variables only as predictors, then specify a formula usingformula.If
Tbldoes not contain the response variable, then specify the response data usingY. The length of response variable and the number of rows ofTblmust be equal.
Note
To save memory and execution time, supply X and Y instead
of Tbl.
Data Types: table
Response variable name, specified as the name of the response variable in
Tbl.
You must specify ResponseVarName as a character
vector or string scalar. For example, if Tbl.Y is the
response variable, then specify ResponseVarName as
'Y'. Otherwise, fitrensemble
treats all columns of Tbl as predictor
variables.
Data Types: char | string
Explanatory model of the response variable and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y~x1+x2+x3". In this form, Y represents the
response variable, and x1, x2, and
x3 represent the predictor variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Predictor data, specified as numeric matrix.
Each row corresponds to one observation, and each column corresponds to one predictor variable.
The length of Y and the number of rows
of X must be equal.
To specify the names of the predictors in the order of their
appearance in X, use the PredictorNames name-value
pair argument.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'NumLearningCycles',500,'Method','Bag','Learners',templateTree(),'CrossVal','on'
cross-validates an ensemble of 500 bagged regression trees using 10-fold
cross-validation.
Note
You cannot use any cross-validation name-value argument together with the
OptimizeHyperparameters name-value argument. You can modify the
cross-validation for OptimizeHyperparameters only by using the
HyperparameterOptimizationOptions name-value argument.
General Ensemble Options
Ensemble aggregation method, specified as the comma-separated pair
consisting of 'Method' and
'LSBoost' or
'Bag'.
| Value | Method | Notes |
|---|---|---|
'LSBoost' | Least-squares boosting (LSBoost) | You can specify the learning rate for shrinkage
by using the 'LearnRate'
name-value pair argument. |
'Bag' | Bootstrap aggregation (bagging, for example, random forest [2]) | fitrensemble uses bagging
with random predictor selections at each split
(random forest) by default. To use bagging without
the random selections, use tree learners whose
'NumVariablesToSample' value is
'all'. |
For details about ensemble aggregation algorithms and examples, see Algorithms, Ensemble Algorithms, and Choose an Applicable Ensemble Aggregation Method.
Example: 'Method','Bag'
Number of ensemble learning cycles, specified as the comma-separated
pair consisting of 'NumLearningCycles' and a positive
integer. At every learning cycle, the software trains one weak learner
for every template object in Learners.
Consequently, the software trains
NumLearningCycles*numel(Learners)
learners.
The software composes the ensemble using all trained learners and
stores them in Mdl.Trained.
For more details, see Tips.
Example: 'NumLearningCycles',500
Data Types: single | double
Weak learners to use in the ensemble, specified as the comma-separated
pair consisting of 'Learners' and
'tree', a tree template object, or a cell vector
of tree template objects.
'tree'(default) —fitrensembleuses default regression tree learners, which is the same as usingtemplateTree(). The default values oftemplateTree()depend on the value of'Method'.For bagged decision trees, the maximum number of decision splits (
'MaxNumSplits') isn–1, wherenis the number of observations. The number of predictors to select at random for each split ('NumVariablesToSample') is one third of the number of predictors. Therefore,fitrensemblegrows deep decision trees. You can grow shallower trees to reduce model complexity or computation time.For boosted decision trees,
'MaxNumSplits'is 10 and'NumVariablesToSample'is'all'. Therefore,fitrensemblegrows shallow decision trees. You can grow deeper trees for better accuracy.
See
templateTreefor the default settings of a weak learner.Tree template object —
fitrensembleuses the tree template object created bytemplateTree. Use the name-value pair arguments oftemplateTreeto specify settings of the tree learners.Cell vector of m tree template objects —
fitrensemblegrows m regression trees per learning cycle (seeNumLearningCycles). For example, for an ensemble composed of two types of regression trees, supply{t1 t2}, wheret1andt2are regression tree template objects returned bytemplateTree.
To obtain reproducible results, you must specify the 'Reproducible' name-value pair argument of
templateTree as true if
'NumVariablesToSample' is not
'all'.
For details on the number of learners to train, see
NumLearningCycles and Tips.
Example: 'Learners',templateTree('MaxNumSplits',5)
Printout frequency, specified as a positive integer or "off".
To track the number of weak learners or folds that
fitrensemble trained so far, specify a positive integer. That
is, if you specify the positive integer m:
Without also specifying any cross-validation option (for example,
CrossVal), thenfitrensembledisplays a message to the command line every time it completes training m weak learners.And a cross-validation option, then
fitrensembledisplays a message to the command line every time it finishes training m folds.
If you specify "off", then fitrensemble does not
display a message when it completes training weak learners.
Tip
For fastest training of some boosted decision trees, set NPrint to the
default value "off". This tip holds when the classification
Method is "AdaBoostM1",
"AdaBoostM2", "GentleBoost", or
"LogitBoost", or when the regression Method is
"LSBoost".
Example: NPrint=5
Data Types: single | double | char | string
Number of bins for numeric predictors, specified as a positive integer scalar.
If the
NumBinsvalue is empty (default), thenfitrensembledoes not bin any predictors.If you specify the
NumBinsvalue as a positive integer scalar (numBins), thenfitrensemblebins every numeric predictor into at mostnumBinsequiprobable bins, and then grows trees on the bin indices instead of the original data.The number of bins can be less than
numBinsif a predictor has fewer thannumBinsunique values.fitrensembledoes not bin categorical predictors.
When you use a large training data set, this binning option speeds up training but might cause
a potential decrease in accuracy. You can try "NumBins",50 first, and
then change the value depending on the accuracy and training speed.
A trained model stores the bin edges in the BinEdges property.
Example: "NumBins",50
Data Types: single | double
Categorical predictors list, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the predictor data is a table
(Tbl), fitrensemble assumes that a variable is
categorical if it is a logical vector, unordered categorical vector, character array, string
array, or cell array of character vectors. If the predictor data is a matrix
(X), fitrensemble assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
Example: 'CategoricalPredictors','all'
Data Types: single | double | logical | char | string | cell
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the column order ofX. That is,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitrensembleuses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
Response variable name, specified as a character vector or string scalar.
If you supply
Y, then you can useResponseNameto specify a name for the response variable.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: ResponseName="response"
Data Types: char | string
Function for transforming raw response values, specified as a function handle or
function name. The default is "none", which means
@(y)y, or no transformation. The function should accept a vector
(the original response values) and return a vector of the same size (the transformed
response values).
Example: Suppose you create a function handle that applies an exponential
transformation to an input vector by using myfunction = @(y)exp(y).
Then, you can specify the response transformation as
ResponseTransform=myfunction.
Data Types: char | string | function_handle
Parallel Options
Options for computing in parallel and setting random numbers, specified as a structure. Create
the Options structure using statset.
Note
You need Parallel Computing Toolbox™ to run computations in parallel.
This table describes the option fields and their values.
| Field Name | Value | Default |
|---|---|---|
UseParallel | Set this value to | false |
UseSubstreams | Set this value to To compute reproducibly, set
| false |
Streams | Specify this value as a RandStream object or cell array of such objects. Use a single object except when the UseParallel value is true and the UseSubstreams value is false. In that case, use a cell array that has the same size as the parallel pool. | If you do not specify Streams, fitrensemble uses the
default stream or streams. |
For an example using reproducible parallel training, see Train Classification Ensemble in Parallel.
For dual-core systems and above, fitrensemble parallelizes
training using Intel® Threading Building Blocks (TBB). Therefore, specifying the
UseParallel option as true might not provide a
significant speedup on a single computer. For details on Intel TBB, see https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.html.
Example: Options=statset(UseParallel=true)
Data Types: struct
Cross-Validation Options
Cross-validation flag, specified as the comma-separated pair
consisting of 'Crossval' and 'on' or 'off'.
If you specify 'on', then the software implements
10-fold cross-validation.
To override this cross-validation setting, use one of these
name-value pair arguments: CVPartition, Holdout, KFold,
or Leaveout. To create a cross-validated model,
you can use one cross-validation name-value pair argument at a time
only.
Alternatively, cross-validate later by passing Mdl to crossval.
Example: 'Crossval','on'
Cross-validation partition, specified as a cvpartition object that specifies the type of cross-validation and the
indexing for the training and validation sets.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Suppose you create a random partition for 5-fold cross-validation on 500
observations by using cvp = cvpartition(500,KFold=5). Then, you can
specify the cross-validation partition by setting
CVPartition=cvp.
Fraction of the data used for holdout validation, specified as a scalar value in the range
(0,1). If you specify Holdout=p, then the software completes these
steps:
Randomly select and reserve
p*100% of the data as validation data, and train the model using the rest of the data.Store the compact trained model in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Holdout=0.1
Data Types: double | single
Number of folds to use in the cross-validated model, specified as a positive integer value
greater than 1. If you specify KFold=k, then the software completes
these steps:
Randomly partition the data into
ksets.For each set, reserve the set as validation data, and train the model using the other
k– 1 sets.Store the
kcompact trained models in ak-by-1 cell vector in theTrainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: KFold=5
Data Types: single | double
Leave-one-out cross-validation flag, specified as "on" or
"off". If you specify Leaveout="on", then for
each of the n observations (where n is the number
of observations, excluding missing observations, specified in the
NumObservations property of the model), the software completes
these steps:
Reserve the one observation as validation data, and train the model using the other n – 1 observations.
Store the n compact trained models in an n-by-1 cell vector in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can specify only one of these four name-value
arguments: CVPartition, Holdout,
KFold, or Leaveout.
Example: Leaveout="on"
Data Types: char | string
Other Regression Options
Observation weights, specified as the comma-separated pair consisting
of 'Weights' and a numeric vector of positive values
or name of a variable in Tbl. The software weighs
the observations in each row of X or
Tbl with the corresponding value in
Weights. The size of Weights
must equal the number of rows of X or
Tbl.
If you specify the input data as a table Tbl,
then Weights can be the name of a variable in
Tbl that contains a numeric vector. In this
case, you must specify Weights as a character
vector or string scalar. For example, if the weights vector
W is stored as Tbl.W, then
specify it as 'W'. Otherwise, the software treats all
columns of Tbl, including W, as
predictors or the response when training the model.
By default, Weights is
ones(, where
n,1)n is the number of observations in
X or Tbl.
The software normalizes the values of Weights to
sum to 1. Inf weights are not supported.
Data Types: double | single | char | string
Sampling Options
Fraction of the training set to resample for every weak learner, specified as a positive
scalar in (0,1]. To use 'FResample', set
Resample to 'on'.
Example: 'FResample',0.75
Data Types: single | double
Flag indicating sampling with replacement, specified as the
comma-separated pair consisting of 'Replace' and 'off' or 'on'.
For
'on', the software samples the training observations with replacement.For
'off', the software samples the training observations without replacement. If you setResampleto'on', then the software samples training observations assuming uniform weights. If you also specify a boosting method, then the software boosts by reweighting observations.
Unless you set Method to 'bag' or
set Resample to 'on', Replace has
no effect.
Example: 'Replace','off'
Flag indicating to resample, specified as the comma-separated
pair consisting of 'Resample' and 'off' or 'on'.
If
Methodis a boosting method, then:'Resample','on'specifies to sample training observations using updated weights as the multinomial sampling probabilities.'Resample','off'(default) specifies to reweight observations at every learning iteration.
If
Methodis'bag', then'Resample'must be'on'. The software resamples a fraction of the training observations (seeFResample) with or without replacement (seeReplace).
If you specify to resample using Resample, then it is good
practice to resample to entire data set. That is, use the default setting of 1 for
FResample.
LSBoost Method Options
Learning rate for shrinkage, specified as the comma-separated pair consisting of
'LearnRate' and a numeric scalar in the interval (0,1].
To train an ensemble using shrinkage, set LearnRate to a value less than 1, for example, 0.1 is a popular choice. Training an ensemble using shrinkage requires more learning iterations, but often achieves better accuracy.
Example: 'LearnRate',0.1
Data Types: single | double
Hyperparameter Optimization Options
Parameters to optimize, specified as the comma-separated pair
consisting of 'OptimizeHyperparameters' and one of
the following:
'none'— Do not optimize.'auto'— Use{'Method','NumLearningCycles','LearnRate'}along with the default parameters for the specifiedLearners:Learners='tree'(default) —{'MinLeafSize'}
Note
For hyperparameter optimization,
Learnersmust be a single argument, not a string array or cell array.'all'— Optimize all eligible parameters.String array or cell array of eligible parameter names
Vector of
optimizableVariableobjects, typically the output ofhyperparameters
The optimization attempts to minimize the cross-validation loss
(error) for fitrensemble by varying the parameters. To control the
cross-validation type and other aspects of the optimization, use the
HyperparameterOptimizationOptions name-value argument. When you use
HyperparameterOptimizationOptions, you can use the (compact) model size
instead of the cross-validation loss as the optimization objective by setting the
ConstraintType and ConstraintBounds options.
Note
The values of OptimizeHyperparameters override any values you
specify using other name-value arguments. For example, setting
OptimizeHyperparameters to "auto" causes
fitrensemble to optimize hyperparameters corresponding to the
"auto" option and to ignore any specified values for the
hyperparameters.
The eligible parameters for fitrensemble
are:
Method— Eligible methods are'Bag'or'LSBoost'.NumLearningCycles—fitrensemblesearches among positive integers, by default log-scaled with range[10,500].LearnRate—fitrensemblesearches among positive reals, by default log-scaled with range[1e-3,1].MinLeafSize—fitrensemblesearches among integers log-scaled in the range[1,max(2,floor(NumObservations/2))].MaxNumSplits—fitrensemblesearches among integers log-scaled in the range[1,max(2,NumObservations-1)].NumVariablesToSample—fitrensemblesearches among integers in the range[1,max(2,NumPredictors)].
Set nondefault parameters by passing a vector of
optimizableVariable objects that have nondefault
values. For example,
load carsmall params = hyperparameters('fitrensemble',[Horsepower,Weight],MPG,'Tree'); params(4).Range = [1,20];
Pass params as the value of
OptimizeHyperparameters.
By default, the iterative display appears at the command line,
and plots appear according to the number of hyperparameters in the optimization. For the
optimization and plots, the objective function is log(1 + cross-validation loss). To control the iterative display, set the Verbose option
of the HyperparameterOptimizationOptions name-value argument. To control
the plots, set the ShowPlots option of the
HyperparameterOptimizationOptions name-value argument.
For an example, see Optimize Regression Ensemble.
Example: 'OptimizeHyperparameters',{'Method','NumLearningCycles','LearnRate','MinLeafSize','MaxNumSplits'}
Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument
modifies the effect of the OptimizeHyperparameters name-value
argument. If you specify HyperparameterOptimizationOptions, you must
also specify OptimizeHyperparameters. All the options are optional.
However, you must set ConstraintBounds and
ConstraintType to return
AggregateOptimizationResults. The options that you can set in a
structure are the same as those in the
HyperparameterOptimizationOptions object.
| Option | Values | Default |
|---|---|---|
Optimizer |
| "bayesopt" |
ConstraintBounds | Constraint bounds for N optimization problems,
specified as an N-by-2 numeric matrix or
| [] |
ConstraintTarget | Constraint target for the optimization problems, specified as
| If you specify ConstraintBounds and
ConstraintType, then the default value is
"matlab". Otherwise, the default value is
[]. |
ConstraintType | Constraint type for the optimization problems, specified as
| [] |
AcquisitionFunctionName | Type of acquisition function:
Acquisition functions whose names include
| "expected-improvement-per-second-plus" |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. If you specify multiple
optimization problems using ConstraintBounds, the value of
MaxObjectiveEvaluations applies to each optimization
problem individually. | 30 for "bayesopt" and
"randomsearch", and the entire grid for
"gridsearch" |
MaxTime | Time limit for the optimization, specified as a nonnegative real
scalar. The time limit is in seconds, as measured by | Inf |
NumGridDivisions | For Optimizer="gridsearch", the number of values in each
dimension. The value can be a vector of positive integers giving the number of
values for each dimension, or a scalar that applies to all dimensions. The
software ignores this option for categorical variables. | 10 |
ShowPlots | Logical value indicating whether to show plots of the optimization progress.
If this option is true, the software plots the best observed
objective function value against the iteration number. If you use Bayesian
optimization (Optimizer="bayesopt"), the
software also plots the best estimated objective function value. The best
observed objective function values and best estimated objective function values
correspond to the values in the BestSoFar (observed) and
BestSoFar (estim.) columns of the iterative display,
respectively. You can find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of
Mdl.HyperparameterOptimizationResults. If the problem
includes one or two optimization parameters for Bayesian optimization, then
ShowPlots also plots a model of the objective function
against the parameters. | true |
SaveIntermediateResults | Logical value indicating whether to save the optimization results. If this
option is true, the software overwrites a workspace variable
named "BayesoptResults" at each iteration. The variable is a
BayesianOptimization object. If you
specify multiple optimization problems using
ConstraintBounds, the workspace variable is an AggregateBayesianOptimization object named
"AggregateBayesoptResults". | false |
Verbose | Display level at the command line:
For details, see the | 1 |
UseParallel | Logical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization. | false |
Repartition | Logical value indicating whether to repartition the cross-validation at
every iteration. If this option is A value of
| false |
| Specify only one of the following three options. | ||
CVPartition | cvpartition object created by cvpartition | KFold=5 if you do not specify a
cross-validation option |
Holdout | Scalar in the range (0,1) representing the holdout
fraction | |
KFold | Integer greater than 1 | |
Example: HyperparameterOptimizationOptions=struct(UseParallel=true)
Output Arguments
Trained ensemble model, returned as one of the model objects in this table.
| Model Object | Specify Any Cross-Validation Options? | Method
Setting | Resample
Setting |
|---|---|---|---|
RegressionBaggedEnsemble | No | 'Bag' | 'on' |
RegressionEnsemble | No | 'LSBoost' | 'off' |
RegressionPartitionedEnsemble | Yes | 'LSBoost' or
'Bag' | 'off' or
'on' |
The name-value pair arguments that control cross-validation
are CrossVal, Holdout,
KFold, Leaveout, and
CVPartition.
To reference properties of Mdl, use dot notation. For
example, to access or display the cell vector of weak learner model objects
for an ensemble that has not been cross-validated, enter
Mdl.Trained at the command line.
If you specify OptimizeHyperparameters and
set the ConstraintType and ConstraintBounds options of
HyperparameterOptimizationOptions, then Mdl is an
N-by-1 cell array of model objects, where N is equal
to the number of rows in ConstraintBounds. If none of the optimization
problems yields a feasible model, then each cell array value is [].
Aggregate optimization results for multiple optimization problems, returned as an AggregateBayesianOptimization object. To return
AggregateOptimizationResults, you must specify
OptimizeHyperparameters and
HyperparameterOptimizationOptions. You must also specify the
ConstraintType and ConstraintBounds
options of HyperparameterOptimizationOptions. For an example that
shows how to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.
Tips
NumLearningCyclescan vary from a few dozen to a few thousand. Usually, an ensemble with good predictive power requires from a few hundred to a few thousand weak learners. However, you do not have to train an ensemble for that many cycles at once. You can start by growing a few dozen learners, inspect the ensemble performance and then, if necessary, train more weak learners usingresume.Ensemble performance depends on the ensemble setting and the setting of the weak learners. That is, if you specify weak learners with default parameters, then the ensemble can perform poorly. Therefore, like ensemble settings, it is good practice to adjust the parameters of the weak learners using templates, and to choose values that minimize generalization error.
If you specify to resample using
Resample, then it is good practice to resample to entire data set. That is, use the default setting of1forFResample.After training a model, you can generate C/C++ code that predicts responses for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
For details of ensemble aggregation algorithms, see Ensemble Algorithms.
If you specify
'Method','LSBoost', then the software grows shallow decision trees by default. You can adjust tree depth by specifying theMaxNumSplits,MinLeafSize, andMinParentSizename-value pair arguments usingtemplateTree.For dual-core systems and above,
fitrensembleparallelizes training using Intel Threading Building Blocks (TBB). For details on Intel TBB, see https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.html.
References
[1] Breiman, L. “Bagging Predictors.” Machine Learning. Vol. 26, pp. 123–140, 1996.
[2] Breiman, L. “Random Forests.” Machine Learning. Vol. 45, pp. 5–32, 2001.
[3] Freund, Y. and R. E. Schapire. “A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting.” J. of Computer and System Sciences, Vol. 55, pp. 119–139, 1997.
[4] Friedman, J. “Greedy function approximation: A gradient boosting machine.” Annals of Statistics, Vol. 29, No. 5, pp. 1189–1232, 2001.
[5] Hastie, T., R. Tibshirani, and J. Friedman. The Elements of Statistical Learning section edition, Springer, New York, 2008.
Extended Capabilities
fitrensemble supports parallel training
using the 'Options' name-value argument. Create options using statset, such as options = statset('UseParallel',true).
Parallel ensemble training requires you to set the 'Method' name-value
argument to 'Bag'. Parallel training is available only for tree learners, the
default type for 'Bag'.
To perform parallel hyperparameter optimization, use the UseParallel=true
option in the HyperparameterOptimizationOptions name-value argument in
the call to the fitrensemble function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Usage notes and limitations:
fitrensembledoes not support bootstrap aggregation. You can specify the name-value argumentMethodonly as"LSBoost".If you use
templateTreeto create a learner template object or cell vector of learner template objects, you can specify the name-value argumentsSurrogateandPredictorSelectiononly as"off"and"allsplits", respectively.If you use
templateTreeand the data contains categorical predictors, you can specify the name-value argumentNumVariablesToSampleonly as"all".fitrensemblefits the model on a GPU if at least one of the following applies:The input argument
Xis agpuArrayobject.The input argument
Yis agpuArrayobject.The input argument
TblcontainsgpuArraypredictor or response variables.
If you use
templateTreeto specifyMaxNumSplits, note thatfitrensemblemight not execute faster on a GPU than a CPU for deeper decision trees.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2016bfitrensemble defaults to serial hyperparameter optimization when
HyperparameterOptimizationOptions includes
UseParallel=true and the software cannot open a parallel pool.
In previous releases, the software issues an error under these circumstances.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)