templateTree
Create decision tree template
Description
t = templateTreet as a learner using:
fitcensemblefor classification ensemblesfitrensemblefor regression ensemblesfitcecocfor ECOC model classification
If you specify a default decision tree template, then the software uses default values for all input arguments during training. It is good practice to specify the type of decision tree, e.g., for a classification tree template, specify 'Type','classification'. If you specify the type of decision tree and display t in the Command Window, then all options except Type appear empty ([]).
t = templateTree(Name,Value)
For example, you can specify the algorithm used to find the best split on a categorical predictor, the split criterion, or the number of predictors selected for each split.
If you display t in the Command Window, then all options appear empty ([]), except those that you specify using name-value pair arguments. During training, the software uses default values for empty options.
Examples
Create a decision tree template with surrogate splits, and use the template to train an ensemble using sample data.
Load Fisher's iris data set.
load fisheririsCreate a decision tree template of tree stumps with surrogate splits.
t = templateTree('Surrogate','on','MaxNumSplits',1)
t =
Fit template for Tree.
Surrogate: 'on'
MaxNumSplits: 1
Options for the template object are empty except for Surrogate and MaxNumSplits. When you pass t to the training function, the software fills in the empty options with their respective default values.
Specify t as a weak learner for a classification ensemble.
Mdl = fitcensemble(meas,species,'Method','AdaBoostM2','Learners',t)
Mdl =
ClassificationEnsemble
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
NumTrained: 100
Method: 'AdaBoostM2'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [100×1 double]
FitInfoDescription: {2×1 cell}
Properties, Methods
Display the in-sample (resubstitution) misclassification error.
L = resubLoss(Mdl)
L = 0.0333
One way to create an ensemble of boosted regression trees that has satisfactory predictive performance is to tune the decision tree complexity level using cross-validation. While searching for an optimal complexity level, tune the learning rate to minimize the number of learning cycles as well.
This example manually finds optimal parameters by using the cross-validation option (the 'KFold' name-value pair argument) and the kfoldLoss function. Alternatively, you can use the 'OptimizeHyperparameters' name-value pair argument to optimize hyperparameters automatically. See Optimize Regression Ensemble.
Load the carsmall data set. Choose the number of cylinders, volume displaced by the cylinders, horsepower, and weight as predictors of fuel economy.
load carsmall
Tbl = table(Cylinders,Displacement,Horsepower,Weight,MPG);The default values of the tree depth controllers for boosting regression trees are:
10forMaxNumSplits.5forMinLeafSize10forMinParentSize
To search for the optimal tree-complexity level:
Cross-validate a set of ensembles. Exponentially increase the tree-complexity level for subsequent ensembles from decision stump (one split) to at most n - 1 splits. n is the sample size. Also, vary the learning rate for each ensemble between 0.1 to 1.
Estimate the cross-validated mean-squared error (MSE) for each ensemble.
For tree-complexity level , , compare the cumulative, cross-validated MSE of the ensembles by plotting them against number of learning cycles. Plot separate curves for each learning rate on the same figure.
Choose the curve that achieves the minimal MSE, and note the corresponding learning cycle and learning rate.
Cross-validate a deep regression tree and a stump. Because the data contain missing values, use surrogate splits. These regression trees serve as benchmarks.
rng(1) % For reproducibility MdlDeep = fitrtree(Tbl,'MPG','CrossVal','on','MergeLeaves','off', ... 'MinParentSize',1,'Surrogate','on'); MdlStump = fitrtree(Tbl,'MPG','MaxNumSplits',1,'CrossVal','on', ... 'Surrogate','on');
Cross-validate an ensemble of 150 boosted regression trees using 5-fold cross-validation. Using a tree template:
Vary the maximum number of splits using the values in the sequence . m is such that is no greater than n - 1.
Turn on surrogate splits.
For each variant, adjust the learning rate using each value in the set {0.1, 0.25, 0.5, 1}.
n = size(Tbl,1); m = floor(log2(n - 1)); learnRate = [0.1 0.25 0.5 1]; numLR = numel(learnRate); maxNumSplits = 2.^(0:m); numMNS = numel(maxNumSplits); numTrees = 150; Mdl = cell(numMNS,numLR); for k = 1:numLR for j = 1:numMNS t = templateTree('MaxNumSplits',maxNumSplits(j),'Surrogate','on'); Mdl{j,k} = fitrensemble(Tbl,'MPG','NumLearningCycles',numTrees, ... 'Learners',t,'KFold',5,'LearnRate',learnRate(k)); end end
Estimate the cumulative, cross-validated MSE of each ensemble.
kflAll = @(x)kfoldLoss(x,'Mode','cumulative'); errorCell = cellfun(kflAll,Mdl,'Uniform',false); error = reshape(cell2mat(errorCell),[numTrees numel(maxNumSplits) numel(learnRate)]); errorDeep = kfoldLoss(MdlDeep); errorStump = kfoldLoss(MdlStump);
Plot how the cross-validated MSE behaves as the number of trees in the ensemble increases. Plot the curves with respect to learning rate on the same plot, and plot separate plots for varying tree-complexity levels. Choose a subset of tree complexity levels to plot.
mnsPlot = [1 round(numel(maxNumSplits)/2) numel(maxNumSplits)]; figure; for k = 1:3 subplot(2,2,k) plot(squeeze(error(:,mnsPlot(k),:)),'LineWidth',2) axis tight hold on h = gca; plot(h.XLim,[errorDeep errorDeep],'-.b','LineWidth',2) plot(h.XLim,[errorStump errorStump],'-.r','LineWidth',2) plot(h.XLim,min(min(error(:,mnsPlot(k),:))).*[1 1],'--k') h.YLim = [10 50]; xlabel('Number of trees') ylabel('Cross-validated MSE') title(sprintf('MaxNumSplits = %0.3g', maxNumSplits(mnsPlot(k)))) hold off end hL = legend([cellstr(num2str(learnRate','Learning Rate = %0.2f')); ... 'Deep Tree';'Stump';'Min. MSE']); hL.Position(1) = 0.6;
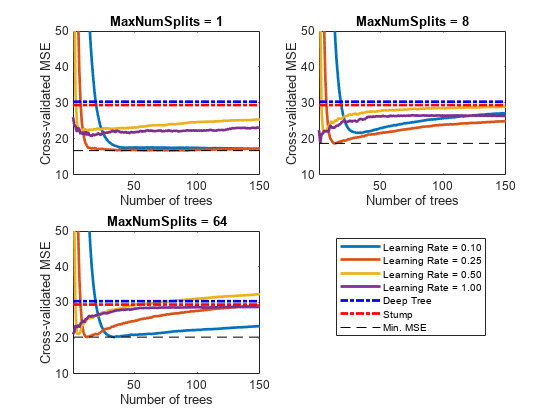
Each curve contains a minimum cross-validated MSE occurring at the optimal number of trees in the ensemble.
Identify the maximum number of splits, number of trees, and learning rate that yields the lowest MSE overall.
[minErr,minErrIdxLin] = min(error(:));
[idxNumTrees,idxMNS,idxLR] = ind2sub(size(error),minErrIdxLin);
fprintf('\nMin. MSE = %0.5f',minErr)Min. MSE = 16.77593
fprintf('\nOptimal Parameter Values:\nNum. Trees = %d',idxNumTrees);Optimal Parameter Values: Num. Trees = 78
fprintf('\nMaxNumSplits = %d\nLearning Rate = %0.2f\n',... maxNumSplits(idxMNS),learnRate(idxLR))
MaxNumSplits = 1 Learning Rate = 0.25
Create a predictive ensemble based on the optimal hyperparameters and the entire training set.
tFinal = templateTree('MaxNumSplits',maxNumSplits(idxMNS),'Surrogate','on'); MdlFinal = fitrensemble(Tbl,'MPG','NumLearningCycles',idxNumTrees, ... 'Learners',tFinal,'LearnRate',learnRate(idxLR))
MdlFinal =
RegressionEnsemble
PredictorNames: {'Cylinders' 'Displacement' 'Horsepower' 'Weight'}
ResponseName: 'MPG'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
NumTrained: 78
Method: 'LSBoost'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [78×1 double]
FitInfoDescription: {2×1 cell}
Regularization: []
Properties, Methods
MdlFinal is a RegressionEnsemble. To predict the fuel economy of a car given its number of cylinders, volume displaced by the cylinders, horsepower, and weight, you can pass the predictor data and MdlFinal to predict.
Instead of searching optimal values manually by using the cross-validation option ('KFold') and the kfoldLoss function, you can use the 'OptimizeHyperparameters' name-value pair argument. When you specify 'OptimizeHyperparameters', the software finds optimal parameters automatically using Bayesian optimization. The optimal values obtained by using 'OptimizeHyperparameters' can be different from those obtained using manual search.
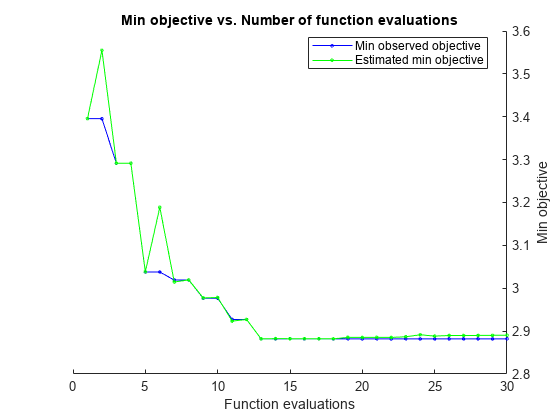
t = templateTree('Surrogate','on'); mdl = fitrensemble(Tbl,'MPG','Learners',t, ... 'OptimizeHyperparameters',{'NumLearningCycles','LearnRate','MaxNumSplits'})
|====================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | NumLearningC-| LearnRate | MaxNumSplits |
| | result | log(1+loss) | runtime | (observed) | (estim.) | ycles | | |
|====================================================================================================================|
| 1 | Best | 3.3955 | 1.3889 | 3.3955 | 3.3955 | 26 | 0.072054 | 3 |
| 2 | Accept | 6.0976 | 5.4197 | 3.3955 | 3.5549 | 170 | 0.0010295 | 70 |
| 3 | Best | 3.2914 | 8.7456 | 3.2914 | 3.2917 | 273 | 0.61026 | 6 |
| 4 | Accept | 6.1839 | 2.6847 | 3.2914 | 3.2915 | 80 | 0.0016871 | 1 |
| 5 | Best | 3.0379 | 0.78465 | 3.0379 | 3.0384 | 18 | 0.21288 | 31 |
| 6 | Accept | 3.3628 | 0.42366 | 3.0379 | 3.1888 | 10 | 0.17826 | 5 |
| 7 | Best | 2.9883 | 0.45569 | 2.9883 | 3.1225 | 10 | 0.27626 | 3 |
| 8 | Accept | 3.0528 | 0.4419 | 2.9883 | 3.102 | 10 | 0.28525 | 83 |
| 9 | Best | 2.9789 | 0.5057 | 2.9789 | 2.975 | 10 | 0.28889 | 4 |
| 10 | Accept | 3.1033 | 0.4265 | 2.9789 | 2.975 | 10 | 0.90615 | 1 |
| 11 | Best | 2.9434 | 0.84123 | 2.9434 | 2.9279 | 22 | 0.42668 | 1 |
| 12 | Accept | 3.0846 | 0.47419 | 2.9434 | 2.9428 | 10 | 0.47213 | 17 |
| 13 | Best | 2.9276 | 3.1248 | 2.9276 | 2.956 | 101 | 0.23375 | 1 |
| 14 | Accept | 3.1607 | 1.2185 | 2.9276 | 3.042 | 32 | 0.34833 | 82 |
| 15 | Accept | 6.1367 | 0.49364 | 2.9276 | 2.9313 | 10 | 0.015396 | 90 |
| 16 | Accept | 5.526 | 0.48262 | 2.9276 | 2.9277 | 10 | 0.046087 | 30 |
| 17 | Best | 2.9196 | 2.6855 | 2.9196 | 2.9195 | 76 | 0.078803 | 1 |
| 18 | Accept | 2.9292 | 1.5843 | 2.9196 | 2.9192 | 46 | 0.13108 | 1 |
| 19 | Accept | 3.0564 | 0.41826 | 2.9196 | 2.922 | 10 | 0.30881 | 21 |
| 20 | Accept | 4.4955 | 0.503 | 2.9196 | 2.9194 | 10 | 0.099393 | 87 |
|====================================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | NumLearningC-| LearnRate | MaxNumSplits |
| | result | log(1+loss) | runtime | (observed) | (estim.) | ycles | | |
|====================================================================================================================|
| 21 | Accept | 3.0934 | 0.97118 | 2.9196 | 2.9192 | 25 | 0.98063 | 2 |
| 22 | Accept | 3.4006 | 0.5528 | 2.9196 | 2.9196 | 10 | 0.98331 | 87 |
| 23 | Accept | 2.9309 | 0.61287 | 2.9196 | 2.9198 | 15 | 0.30805 | 1 |
| 24 | Accept | 2.9966 | 2.1401 | 2.9196 | 2.9196 | 64 | 0.73892 | 1 |
| 25 | Accept | 2.9285 | 0.94985 | 2.9196 | 2.9188 | 26 | 0.22761 | 1 |
| 26 | Best | 2.9052 | 4.704 | 2.9052 | 2.9053 | 146 | 0.12074 | 1 |
| 27 | Accept | 2.9936 | 1.6306 | 2.9052 | 2.906 | 51 | 0.17258 | 6 |
| 28 | Accept | 2.9292 | 5.6109 | 2.9052 | 2.9053 | 164 | 0.043163 | 1 |
| 29 | Best | 2.8925 | 10.047 | 2.8925 | 2.8925 | 311 | 0.0709 | 1 |
| 30 | Accept | 3.0114 | 0.95983 | 2.8925 | 2.8927 | 26 | 0.34547 | 3 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 79.5132 seconds
Total objective function evaluation time: 61.2819
Best observed feasible point:
NumLearningCycles LearnRate MaxNumSplits
_________________ _________ ____________
311 0.0709 1
Observed objective function value = 2.8925
Estimated objective function value = 2.8927
Function evaluation time = 10.0468
Best estimated feasible point (according to models):
NumLearningCycles LearnRate MaxNumSplits
_________________ _________ ____________
311 0.0709 1
Estimated objective function value = 2.8927
Estimated function evaluation time = 9.8137
mdl =
RegressionEnsemble
PredictorNames: {'Cylinders' 'Displacement' 'Horsepower' 'Weight'}
ResponseName: 'MPG'
CategoricalPredictors: []
ResponseTransform: 'none'
NumObservations: 94
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
NumTrained: 311
Method: 'LSBoost'
LearnerNames: {'Tree'}
ReasonForTermination: 'Terminated normally after completing the requested number of training cycles.'
FitInfo: [311×1 double]
FitInfoDescription: {2×1 cell}
Regularization: []
Properties, Methods
Load the carsmall data set. Consider a model that predicts the mean fuel economy of a car given its acceleration, number of cylinders, engine displacement, horsepower, manufacturer, model year, and weight. Consider Cylinders, Mfg, and Model_Year as categorical variables.
load carsmall Cylinders = categorical(Cylinders); Mfg = categorical(cellstr(Mfg)); Model_Year = categorical(Model_Year); X = table(Acceleration,Cylinders,Displacement,Horsepower,Mfg,... Model_Year,Weight,MPG);
Display the number of categories represented in the categorical variables.
numCylinders = numel(categories(Cylinders))
numCylinders = 3
numMfg = numel(categories(Mfg))
numMfg = 28
numModelYear = numel(categories(Model_Year))
numModelYear = 3
Because there are 3 categories only in Cylinders and Model_Year, the standard CART, predictor-splitting algorithm prefers splitting a continuous predictor over these two variables.
Train a random forest of 500 regression trees using the entire data set. To grow unbiased trees, specify usage of the curvature test for splitting predictors. Because there are missing values in the data, specify usage of surrogate splits. To reproduce random predictor selections, set the seed of the random number generator by using rng and specify 'Reproducible',true.
rng('default'); % For reproducibility t = templateTree('PredictorSelection','curvature','Surrogate','on', ... 'Reproducible',true); % For reproducibility of random predictor selections Mdl = fitrensemble(X,'MPG','Method','bag','NumLearningCycles',500, ... 'Learners',t);
Estimate predictor importance measures by permuting out-of-bag observations. Perform calculations in parallel.
options = statset('UseParallel',true); imp = oobPermutedPredictorImportance(Mdl,'Options',options);
Starting parallel pool (parpool) using the 'local' profile ... Connected to the parallel pool (number of workers: 6).
Compare the estimates using a bar graph.
figure; bar(imp); title('Out-of-Bag Permuted Predictor Importance Estimates'); ylabel('Estimates'); xlabel('Predictors'); h = gca; h.XTickLabel = Mdl.PredictorNames; h.XTickLabelRotation = 45; h.TickLabelInterpreter = 'none';

In this case, Model_Year is the most important predictor, followed by Cylinders. Compare these results to the results in Estimate Importance of Predictors.
Create an ensemble template for use in fitcecoc.
Load the arrhythmia data set.
load arrhythmia
tabulate(categorical(Y)); Value Count Percent
1 245 54.20%
2 44 9.73%
3 15 3.32%
4 15 3.32%
5 13 2.88%
6 25 5.53%
7 3 0.66%
8 2 0.44%
9 9 1.99%
10 50 11.06%
14 4 0.88%
15 5 1.11%
16 22 4.87%
rng(1); % For reproducibilitySome classes have small relative frequencies in the data.
Create a template for a AdaBoostM1 ensemble of classification trees, and specify to use 100 learners and a shrinkage of 0.1. By default, boosting grows stumps (i.e., one node having a set of leaves). Since there are classes with small frequencies, the trees must be leafy enough to be sensitive to the minority classes. Specify the minimum number of leaf node observations to 3.
tTree = templateTree('MinLeafSize',20); t = templateEnsemble('AdaBoostM1',100,tTree,'LearnRate',0.1);
All properties of the template objects are empty except for Method and Type, and the corresponding properties of the name-value pair argument values in the function calls. When you pass t to the training function, the software fills in the empty properties with their respective default values.
Specify t as a binary learner for an ECOC multiclass model. Train using the default one-versus-one coding design.
Mdl = fitcecoc(X,Y,'Learners',t);Mdlis aClassificationECOCmulticlass model.Mdl.BinaryLearnersis a 78-by-1 cell array ofCompactClassificationEnsemblemodels.Mdl.BinaryLearners{j}.Trainedis a 100-by-1 cell array ofCompactClassificationTreemodels, forj= 1,...,78.
You can verify that one of the binary learners contains a weak learner that isn't a stump by using view.
view(Mdl.BinaryLearners{1}.Trained{1},'Mode','graph')
Display the in-sample (resubstitution) misclassification error.
L = resubLoss(Mdl,'LossFun','classiferror')
L = 0.0819
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Surrogate','on','NumVariablesToSample','all' specifies a template with surrogate splits, and uses all available predictors at each split.
For Classification Trees and Regression Trees
Maximal number of decision splits (or branch nodes) per tree,
specified as the comma-separated pair consisting of
'MaxNumSplits' and a nonnegative scalar.
templateTree splits
MaxNumSplits or fewer branch nodes. For more
details on splitting behavior, see Algorithms.
For bagged decision trees and decision tree binary learners in ECOC models, the default is n – 1, where n is the number of observations in the training sample. For boosted decision trees, the default is 10.
Example: 'MaxNumSplits',5
Data Types: single | double
Leaf merge flag, specified as the comma-separated pair consisting of 'MergeLeaves' and either 'on' or 'off'.
When 'on', the decision tree merges leaves that
originate from the same parent node, and that provide a sum of risk
values greater than or equal to the risk associated with the parent
node. When 'off', the decision tree does not merge
leaves.
For boosted and bagged decision trees, the defaults are 'off'. For decision tree binary learners in ECOC models, the default is 'on'.
Example: 'MergeLeaves','on'
Minimum observations per leaf, specified as the comma-separated pair consisting of 'MinLeafSize' and a positive integer value. Each leaf has at least MinLeafSize observations per tree leaf. If you supply both MinParentSize and MinLeafSize, the decision tree uses the setting that gives larger leaves: MinParentSize = max(MinParentSize,2*MinLeafSize).
For boosted and bagged decision trees, the defaults are 1 for classification and 5 for regression. For decision tree binary learners in ECOC models, the default is 1.
Example: 'MinLeafSize',2
Minimum observations per branch node, specified as the comma-separated pair consisting of 'MinParentSize' and a positive integer value. Each branch node in the tree has at least MinParentSize observations. If you supply both MinParentSize and MinLeafSize, the decision tree uses the setting that gives larger leaves: MinParentSize = max(MinParentSize,2*MinLeafSize).
If you specify
MinLeafSize, then the default value for'MinParentSize'is10.If you do not specify
MinLeafSize, then the default value changes depending on the training model. For boosted and bagged decision trees, the default value is2for classification and10for regression. For decision tree binary learners in ECOC models, the default value is10.
Example: 'MinParentSize',4
Number of predictors to select at random for each split, specified as the comma-separated pair consisting of 'NumVariablesToSample' and a positive integer value. Alternatively, you can specify 'all' to use all available predictors.
If the training data includes many predictors and you want to analyze predictor
importance, then specify 'NumVariablesToSample' as
'all'. Otherwise, the software might not select some predictors,
underestimating their importance.
To reproduce the random selections, you must set the seed of the random number generator by using rng and specify 'Reproducible',true.
For boosted decision trees and decision tree binary learners in ECOC models, the default is 'all'. The default for bagged decision trees is the square root of the number of predictors for classification, or one third of the number of predictors for regression.
Example: 'NumVariablesToSample',3
Data Types: single | double | char | string
Algorithm used to select the best split predictor at each node, specified as the comma-separated pair consisting of 'PredictorSelection' and a value in this table.
| Value | Description |
|---|---|
'allsplits' | Standard CART — Selects the split predictor that maximizes the split-criterion gain over all possible splits of all predictors [1]. |
'curvature' | Curvature test — Selects the split predictor that minimizes the p-value of chi-square tests of independence between each predictor and the response [3][4]. Training speed is similar to standard CART. |
'interaction-curvature' | Interaction test — Chooses the split predictor that minimizes the p-value of chi-square tests of independence between each predictor and the response, and that minimizes the p-value of a chi-square test of independence between each pair of predictors and response [3]. Training speed can be slower than standard CART. |
For 'curvature' and 'interaction-curvature', if all tests yield p-values greater than 0.05, then MATLAB® stops splitting nodes.
Tip
The curvature and interaction tests are not recommended for boosting decision trees. To train an ensemble of boosted trees that has greater accuracy, use standard CART instead.
Standard CART tends to select split predictors containing many distinct values, e.g., continuous variables, over those containing few distinct values, e.g., categorical variables [4]. If the predictor data set is heterogeneous, or if there are predictors that have relatively fewer distinct values than other variables, then consider specifying the curvature or interaction test.
If there are predictors that have relatively fewer distinct values than other predictors, for example, if the predictor data set is heterogeneous.
If an analysis of predictor importance is your goal. For more on predictor importance estimation, see
oobPermutedPredictorImportancefor classification problems,oobPermutedPredictorImportancefor regression problems, and Introduction to Feature Selection.
Trees grown using standard CART are not sensitive to predictor variable interactions. Also, such trees are less likely to identify important variables in the presence of many irrelevant predictors than the application of the interaction test. Therefore, to account for predictor interactions and identify importance variables in the presence of many irrelevant variables, specify the interaction test [3].
Prediction speed is unaffected by the value of
'PredictorSelection'.
For details on how templateTree selects split predictors, see Node Splitting Rules (classification), Node Splitting Rules (regression), and Choose Split Predictor Selection Technique.
Example: 'PredictorSelection','curvature'
Flag to estimate the optimal sequence of pruned subtrees, specified as the comma-separated pair consisting of 'Prune' and 'on' or 'off'.
If Prune is 'on', then the
software trains the classification tree learners without pruning them,
but estimates the optimal sequence of pruned subtrees for each learner
in the ensemble or decision tree binary learner in ECOC models. If
Prune is 'off' and
MergeLeaves is also 'off',
then the software trains the classification tree learners without
estimating the optimal sequence of pruned subtrees.
For boosted and bagged decision trees, the default is 'off'.
For decision tree binary learners in ECOC models, the default is 'on'.
Example: 'Prune','on'
Pruning criterion, specified as the comma-separated pair consisting of 'PruneCriterion' and a pruning criterion valid for the tree type.
For classification trees, you can specify
'error'(default) or'impurity'. If you specify'impurity', thentemplateTreeuses the impurity measure specified by the'SplitCriterion'name-value pair argument.For regression trees, you can specify only
'mse'(default).
Example: 'PruneCriterion','impurity'
Flag to enforce reproducibility over repeated runs of training a model, specified as the
comma-separated pair consisting of 'Reproducible' and either
false or true.
If 'NumVariablesToSample' is not 'all', then the
software selects predictors at random for each split. To reproduce the random
selections, you must specify 'Reproducible',true and set the seed of
the random number generator by using rng. Note that setting 'Reproducible' to
true can slow down training.
Example: 'Reproducible',true
Data Types: logical
Split criterion, specified as the comma-separated pair consisting of 'SplitCriterion' and a split criterion valid for the tree type.
For classification trees:
'gdi'for Gini's diversity index (default)'twoing'for the twoing rule'deviance'for maximum deviance reduction (also known as cross entropy)
For regression trees:
'mse'for mean squared error (default)
Example: 'SplitCriterion','deviance'
Surrogate decision splits flag, specified as the comma-separated pair consisting of 'Surrogate' and one of 'off', 'on', 'all', or a positive integer value.
When
'off', the decision tree does not find surrogate splits at the branch nodes.When
'on', the decision tree finds at most 10 surrogate splits at each branch node.When set to
'all', the decision tree finds all surrogate splits at each branch node. The'all'setting can consume considerable time and memory.When set to a positive integer value, the decision tree finds at most the specified number of surrogate splits at each branch node.
Use surrogate splits to improve the accuracy of predictions for data with missing values. This setting also lets you compute measures of predictive association between predictors.
Example: 'Surrogate','on'
Data Types: single | double | char | string
Decision tree type, specified as a value in the table
| Value | Description |
|---|---|
'classification' | Grow classification tree learners. The fitting functions fitcensemble and fitcecoc set this value when you pass t to them. |
'regression' | Grow regression tree learners. The fitting function fitrensemble sets this value when you pass t to it. |
Tip
Although t infers Type from the fitting function to which it is supplied, the following occur when you set Type:
The display of
tshows all options. Each unspecified option is an empty array[].templateTreechecks specifications for errors.
Example: 'Type','classification'
Data Types: char | string
For Classification Trees Only
Algorithm to find the best split on a categorical predictor for data with C categories for data and K ≥ 3 classes, specified as the comma-separated pair consisting of 'AlgorithmForCategorical' and one of the following.
| Value | Description |
|---|---|
'Exact' | Consider all 2C–1 – 1 combinations. |
'PullLeft' | Start with all C categories on the right branch. Consider moving each category to the left branch as it achieves the minimum impurity for the K classes among the remaining categories. From this sequence, choose the split that has the lowest impurity. |
'PCA' | Compute a score for each category using the inner product between the first principal component of a weighted covariance matrix (of the centered class probability matrix) and the vector of class probabilities for that category. Sort the scores in ascending order, and consider all C — 1 splits. |
'OVAbyClass' | Start with all C categories on the right branch. For each class, order the categories based on their probability for that class. For the first class, consider moving each category to the left branch in order, recording the impurity criterion at each move. Repeat for the remaining classes. From this sequence, choose the split that has the minimum impurity. |
The software selects the optimal subset of algorithms for each split using the known number of classes and levels of a categorical predictor. For two classes, it always performs the exact search. Use the 'AlgorithmForCategorical' name-value pair argument to specify a particular algorithm.
For more details, see Splitting Categorical Predictors in Classification Trees.
Example: 'AlgorithmForCategorical','PCA'
Maximum category levels in the split node, specified as the comma-separated pair consisting of 'MaxNumCategories' and a nonnegative scalar value. A classification tree splits a categorical predictor using the exact search algorithm if the predictor has at most MaxNumCategories levels in the split node. Otherwise, it finds the best categorical split using one of the inexact algorithms. Note that passing a small value can increase computation time and memory overload.
Example: 'MaxNumCategories',8
For Regression Trees Only
Quadratic error tolerance per node, specified as the comma-separated pair consisting of 'QuadraticErrorTolerance' and a positive scalar value. A regression tree stops splitting nodes when the weighted mean squared error per node drops below QuadraticErrorTolerance*ε, where ε is the weighted mean squared error of all n responses computed before growing the decision tree.
wi is the weight of observation i, given that the weights of all the observations sum to one (), and
is the weighted average of all the responses.
Example: 'QuadraticErrorTolerance',1e-4
Output Arguments
Decision tree template for classification or regression suitable for training an ensemble (boosted and bagged decision trees) or error-correcting output code (ECOC) multiclass model, returned as a template object. Pass t to fitcensemble, or fitrensemble, or fitcecoc to specify how to create the decision tree for the classification ensemble, regression ensemble, or ECOC model, respectively.
If you display t in the Command Window, then all unspecified options appear empty ([]). However, the software replaces empty options with their corresponding default values during training.
Algorithms
To accommodate
MaxNumSplits, the software splits all nodes in the current layer, and then counts the number of branch nodes. A layer is the set of nodes that are equidistant from the root node. If the number of branch nodes exceedsMaxNumSplits, then the software follows this procedure.Determine how many branch nodes in the current layer need to be unsplit so that there would be at most
MaxNumSplitsbranch nodes.Sort the branch nodes by their impurity gains.
Unsplit the desired number of least successful branches.
Return the decision tree grown so far.
This procedure aims at producing maximally balanced trees.
The software splits branch nodes layer by layer until at least one of these events occurs.
There are
MaxNumSplits+ 1 branch nodes.A proposed split causes the number of observations in at least one branch node to be fewer than
MinParentSize.A proposed split causes the number of observations in at least one leaf node to be fewer than
MinLeafSize.The algorithm cannot find a good split within a layer (i.e., the pruning criterion (see
PruneCriterion), does not improve for all proposed splits in a layer). A special case of this event is when all nodes are pure (i.e., all observations in the node have the same class).For values
'curvature'or'interaction-curvature'ofPredictorSelection, all tests yield p-values greater than 0.05.
MaxNumSplitsandMinLeafSizedo not affect splitting at their default values. Therefore, if you set'MaxNumSplits', then splitting might stop due to the value ofMinParentSizebeforeMaxNumSplitssplits occur.For details on selecting split predictors and node-splitting algorithms when growing decision trees, see Algorithms for classification trees and Algorithms for regression trees.
References
[1] Breiman, L., J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Boca Raton, FL: CRC Press, 1984.
[2] Coppersmith, D., S. J. Hong, and J. R. M. Hosking. “Partitioning Nominal Attributes in Decision Trees.” Data Mining and Knowledge Discovery, Vol. 3, 1999, pp. 197–217.
[3] Loh, W.Y. “Regression Trees with Unbiased Variable Selection and Interaction Detection.” Statistica Sinica, Vol. 12, 2002, pp. 361–386.
[4] Loh, W.Y. and Y.S. Shih. “Split Selection Methods for Classification Trees.” Statistica Sinica, Vol. 7, 1997, pp. 815–840.
Version History
Introduced in R2014a
See Also
ClassificationTree | RegressionTree | fitctree | fitcensemble | fitrensemble | fitcecoc | templateEnsemble
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)