taylor
Taylor series
Description
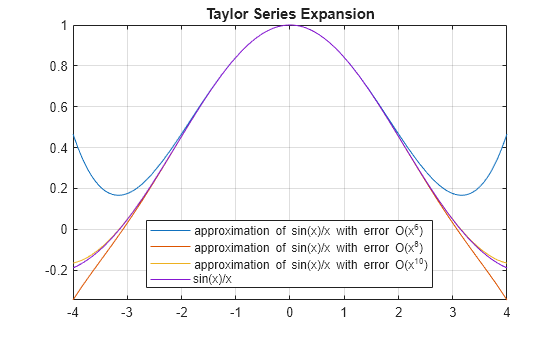
T = taylor(f,var)f with the Taylor series expansion of f up to the fifth order
at the point var = 0. If you do not specify
var, then taylor uses the default
variable determined by symvar(f,1).
T = taylor(___,Name=Value)
Examples
Input Arguments
Name-Value Arguments
More About
Tips
If you use both the third argument
aandExpansionPointto specify the expansion point, then the value specified byExpansionPointprevails.If
varis a vector, then the expansion pointamust be a scalar or a vector of the same length asvar. Ifvaris a vector andais a scalar, thenais expanded into a vector of the same length asvarwith all elements equal toa.If the expansion point is infinity or negative infinity, then
taylorcomputes the Laurent series expansion, which is a power series in1/var.You can use the
sympreffunction to modify the output order of symbolic polynomials.If
taylorcannot find the Taylor series expansion, then useseriesto find the more general Puiseux series expansion.
Version History
Introduced before R2006a