wcoherence
Wavelet coherence and cross-spectrum
Syntax
Description
wcoh = wcoherence(x,y)x and y in the time-frequency plane. Wavelet
coherence is useful for analyzing nonstationary signals. The inputs x and
y must be equal length, 1-D, real-valued signals. The coherence is
computed using the analytic Morlet wavelet.
[___] = wcoherence(___,
specifies options using one or more name-value arguments in addition to the input arguments in
previous syntaxes.Name=Value)
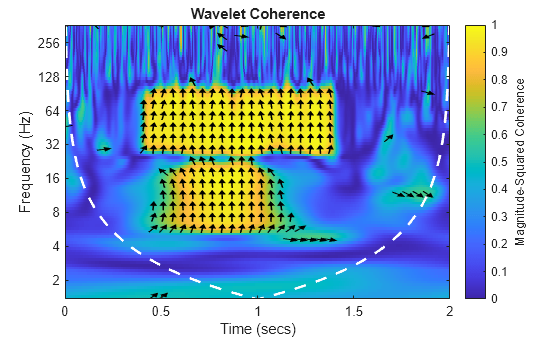
wcoherence(___) with no output
arguments plots the wavelet coherence and cone of influence in the
current figure. Due to the inverse relationship between frequency
and period, a plot that uses the sampling interval is the inverse
of a plot the uses the sampling frequency. For areas where the coherence
exceeds 0.5, plots that use the sampling frequency display arrows
to show the phase lag of y with respect to x.
The arrows are spaced in time and scale. The direction of the arrows
corresponds to the phase lag on the unit circle. For example, a vertical
arrow indicates a π/2 or quarter-cycle phase lag. The corresponding
lag in time depends on the duration of the cycle.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
References
[1] Grinsted, A., J. C. Moore, and S. Jevrejeva. “Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series.” Nonlinear Processes in Geophysics 11, no. 5/6 (November 18, 2004): 561–66. https://doi.org/10.5194/npg-11-561-2004.
[2] Maraun, D., J. Kurths, and M. Holschneider. “Nonstationary Gaussian Processes in Wavelet Domain: Synthesis, Estimation, and Significance Testing.” Physical Review E 75, no. 1 (January 22, 2007): 016707. https://doi.org/10.1103/PhysRevE.75.016707.
[3] Torrence, Christopher, and Peter J. Webster. “Interdecadal Changes in the ENSO–Monsoon System.” Journal of Climate 12, no. 8 (August 1999): 2679–90. https://doi.org/10.1175/1520-0442(1999)012<2679:ICITEM>2.0.CO;2.