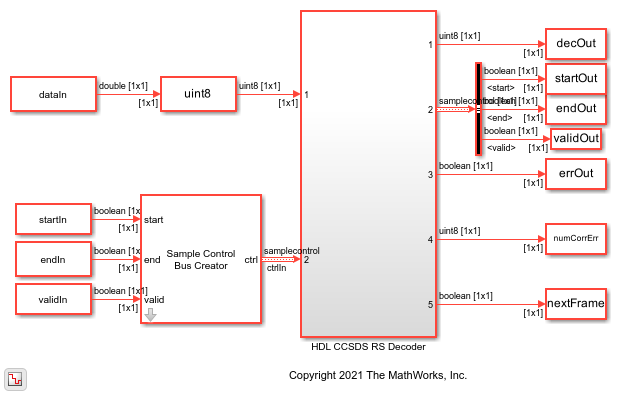
CCSDS RS Decoder
Decode and recover message from RS codeword according to CCSDS standard
Since R2021b
Libraries:
Wireless HDL Toolbox /
Error Detection and Correction
Description
The CCSDS RS Decoder block decodes and recovers a message from a
Reed-Solomon (RS) codeword according to the Consultative Committee for Space Data Systems
(CCSDS) standard [1]. The block accepts codeword
data and a samplecontrol bus and outputs a decoded message data, a
samplecontrol bus, control signals that indicate whether the decoded data
is corrupted and whether the block is ready to accept data, and an optional signal to provide
the number of corrected errors. The block provides an architecture suitable for HDL code
generation and hardware deployment.
Because the latency of the block varies, the block provides the output port nextFrame that indicates when the block is ready to accept new input codeword data. For more details about the latency of the block, see the Algorithm section.
The block also supports shortened message lengths. You can use this block in a CCSDS receiver for satellite communication.
Examples
Ports
Input
Output
Parameters
Algorithms
References
[1] TM Synchronization and Channel Coding. Recommendation for Space Data System Standards. CCSDS 131.0-B-3. Blue Book. Issue 3. Washington, D.C.: CCSDS, September 2017.
[2] TM Synchronization and Channel Coding. Summary of Concept and Rationale CCSDS 130.1-G-3. Green Book. Issue 3, June 2020.
[3] Stephen B. Wicker. Error Control Systems for Digital Communication and Storage. Prentice Hall 1995.
[4] Chien, R. “Cyclic Decoding Procedures for Bose- Chaudhuri-Hocquenghem Codes.” IEEE Transactions on Information Theory 10, no. 4 (October 1964): 357–63. https://doi.org/10.1109/TIT.1964.1053699.
[5] Forney, G. “On Decoding BCH Codes.” IEEE Transactions on Information Theory 11, no. 4 (October 1965): 549–57. https://doi.org/10.1109/TIT.1965.1053825.
Extended Capabilities
Version History
Introduced in R2021b
See Also
Blocks
Functions
ccsdsRSEncode(Satellite Communications Toolbox) |ccsdsRSDecode(Satellite Communications Toolbox)