Symbolic Math Toolbox provides functions for solving, plotting, and manipulating symbolic math equations. You can create, run, and share symbolic math code. In the MATLAB Live Editor, you can get next-step suggestions for symbolic workflows. The toolbox provides functions in common mathematical areas such as calculus, linear algebra, algebraic and differential equations, equation simplification, and equation manipulation.
Symbolic Math Toolbox lets you analytically perform differentiation, integration, simplification, transforms, and equation solving. You can perform dimensional computations and convert between units. Your computations can be performed either analytically or using variable-precision arithmetic, with the results displayed in mathematical typeset.
You can share your symbolic work with other MATLAB users as live scripts or convert them to HTML, Word, LaTeX, or PDF documents. You can generate MATLAB functions, Simulink function blocks, and Simscape equations directly from symbolic expressions.
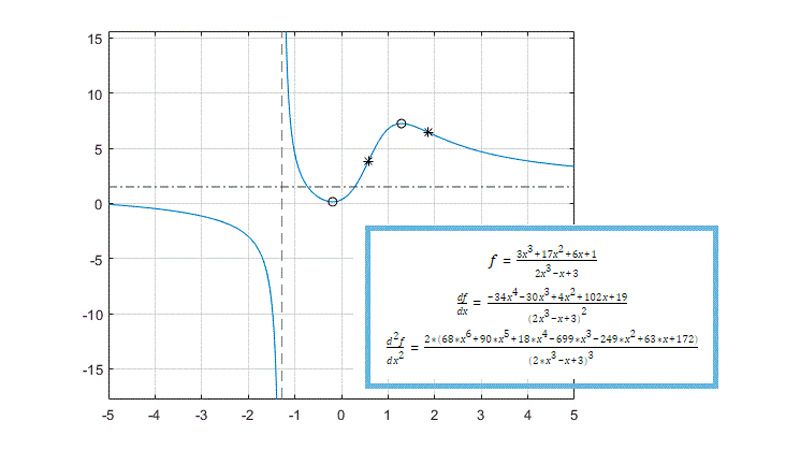
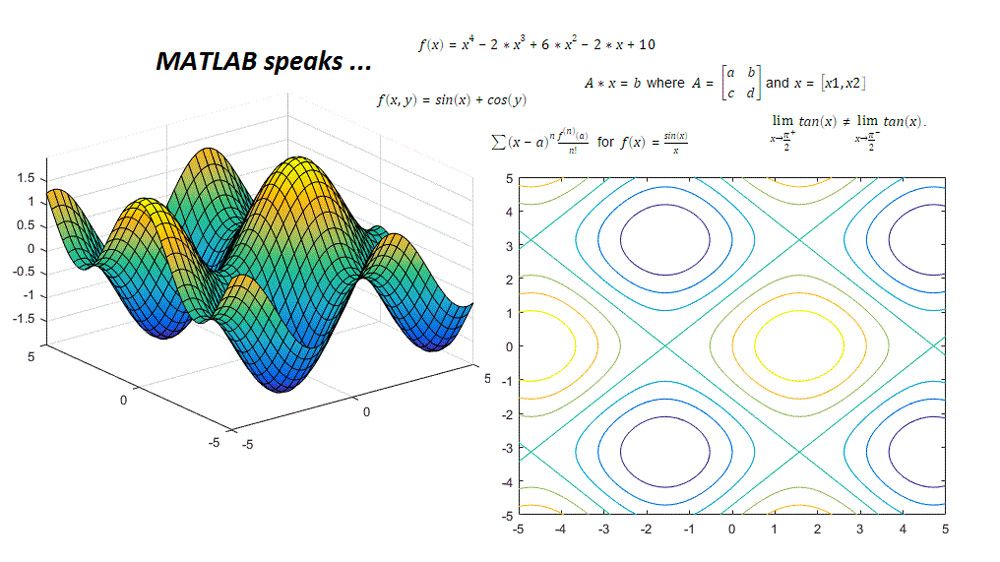
Calculus
Evaluate exact analytical solutions for definite or indefinite integral, calculate derivatives of symbolic expressions or functions, and approximate functions using series expansions.
Linear Algebra
Analyze, transform, and decompose symbolic matrices to study the properties of linear equations, perform linear algebra operations, and solve systems of linear equations in matrix or equation form.
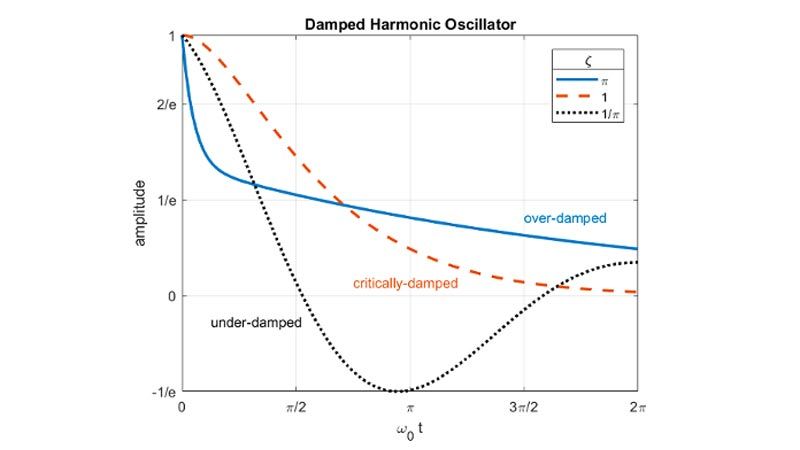
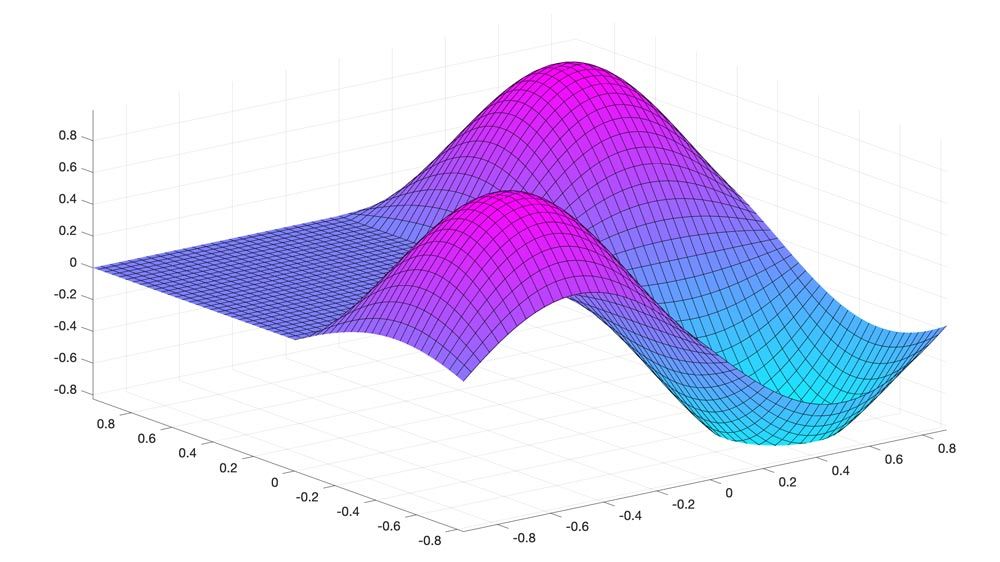
Visualization
Use built-in functions to plot symbolic expressions and functions using extended MATLAB graphics capabilities and visualize the behavior of symbolic expressions using animations.
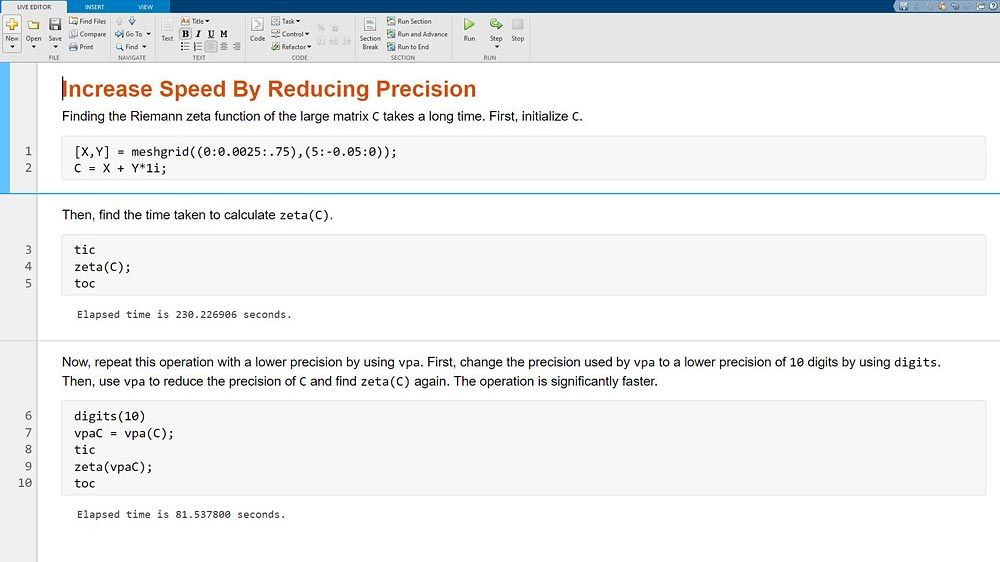
Variable-Precision Arithmetic (VPA)
Explicitly set the number of significant digits to avoid hidden round-off errors. Increase the speed of calculations by reducing the precision with variable-precision arithmetic.
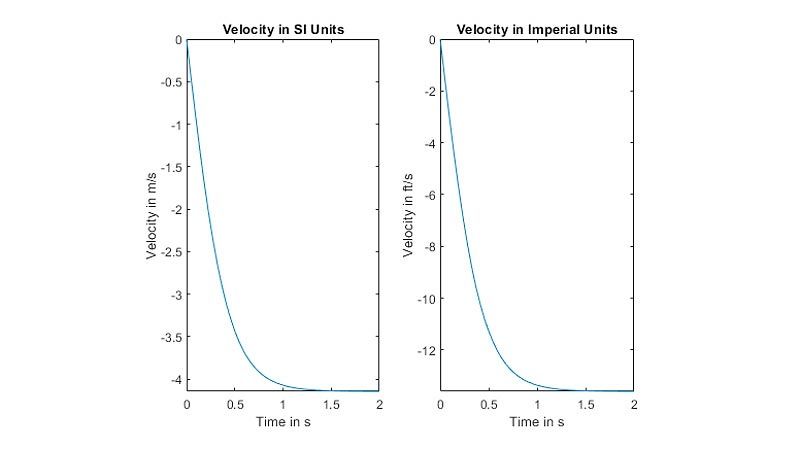
Units and Dimensional Analysis
Perform dimensional analysis and verify the dimensional compatibility and consistency of units in symbolic calculations. Create custom unit systems and convert between existing unit systems.
Documentation and Sharing
Interactively update and display symbolic math computations and get next-step suggestions for symbolic workflows using the MATLAB Live Editor. Share your work as live scripts or publish your code to create formatted documents including HTML, Word, LaTeX, and PDF.
Code Generation
Generate MATLAB functions, Simulink function blocks, custom equation-based Simscape components, and C or Fortran code directly from symbolic expressions.
Product Resources:
Get a Free Trial
30 days of exploration at your fingertips.
Ready to Buy?
Get pricing information and explore related products.
Are You a Student?
Your school may already provide access to MATLAB, Simulink, and add-on products through a campus-wide license.