Practical Course Projects to Introduce Undergraduate Engineering Students to Interface Design and Academic Research
By Peter L. Bishay, California State University Northridge
The courses I teach at California State University, Northridge (CSUN) include Numerical Analysis of Engineering Systems, Computer-Aided Analysis and Design, and Mechanics and Design of Composite Materials. My approach is based on two core principles. First, I train my students to use computer software for their homework assignments and for all engineering problems they encounter. Second, I assign projects that help students develop engineering skills that will serve them for their entire careers, including the ability to work in teams, model engineering systems, read and interpret engineering research papers, and design solutions that address real needs.
Most recently I’ve applied these principles in two junior undergraduate courses: Engineering Computer Applications (at Saint Martin’s University) and Numerical Analysis of Engineering Systems (at CSUN). In both courses, the students completed homework assignments and a weeks-long final project using MATLAB®. The wide variety of available functions and libraries in MATLAB make it easy for students to translate engineering equations into code, which they can then run to understand the effects of various parameters on the solution. The simplicity of the MATLAB programing language, the outstanding control over graphics and plots, and the advanced tools for creating interfaces and apps, also make MATLAB a very attractive platform to use.
Establishing MATLAB Programming Proficiency
To demonstrate the value of MATLAB, in Mechanics and Design of Composite Materials, I recently gave my students the option of completing their coursework either by hand or with MATLAB. Before they made their decision, I gave a quick demonstration. I solved a problem by hand on the board, painstakingly writing out each equation and each step. Next, I showed them how to solve the same problem in MATLAB. Right in front of them, I wrote few lines of MATLAB code that not only solved the problem but also generated plots that they could use to better understand the underlying concepts. Then when I asked them how they would prefer to complete their homework assignments, they all opted for MATLAB.
In both Engineering Computer Applications and Numerical Analysis of Engineering Systems, I devoted several weeks to teaching students how to solve engineering problems by programming in MATLAB. I began with an overview of MATLAB, including the use of matrices, arrays, and cells. I followed that with an introduction to programming concepts in MATLAB, including functions, loops, conditionals, and logical expressions. The Engineering Computer Applications course also included lessons on creating interfaces and using symbolic math in MATLAB. For the Numerical Analysis of Engineering Systems course I omitted these lessons in favor of more detailed lessons on linear algebra, differential equations, numerical differentiation and integration, and eigenvalue problems. After each lesson, the students completed homework assignments in MATLAB.
Course Project: Developing Engineering Applications
For the course project in Engineering Computer Applications, students worked in teams of two or three to develop an application that solved any class of problems on the Fundamentals of Engineering (FE) exam. The topics included mechanics of materials, thermodynamics, fluid mechanics, and mathematics. One of my objectives in choosing this project was to encourage students to think as designers. I wanted them to see that the applications they were developing could be used by their classmates, design engineers, or by MATLAB users worldwide (via the MATLAB Central File Exchange). Hence, I asked them to do their best to make their apps robust and user-friendly. I also asked them to create manuals to help users understand how the apps work and which equations are used. The project gave students an opportunity to refresh their understanding of engineering concepts they had learned earlier in preparation for the FE exam.
In the eighth week of the course, student teams submitted proposals for the applications they wanted to develop. Once their proposals were approved, they had about seven weeks to complete the development of their robust applications, including an interface and documentation for each app.
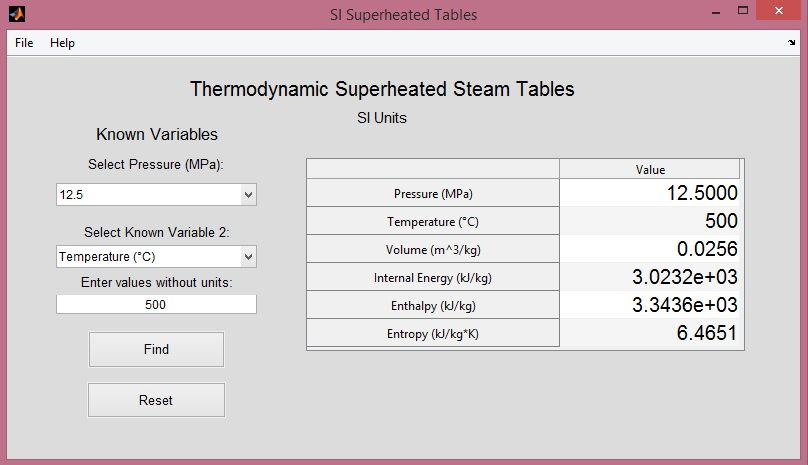
I was amazed at the quality and ingenuity of the applications the student teams created. One team created an application that calculates and plots Mohr’s circles based on input stress values provided by the user (Figure 1). Another created an application that calculates superheated steam table values based on a specified pressure and one other variable, such as temperature, volume, internal energy, enthalpy, or entropy (Figure 2). Other projects included applications that calculate moments of inertia, currents in RCL, or resistor circuits.
An end-of-class survey showed that students felt they had strongly benefited from these projects. One student commented, “The project took a problem and addressed it from start to finish by determining the necessary formula(s), coding them in MATLAB, developing a GUI, writing a user manual, etc. It was about as perfect and helpful toward learning as a school project could possibly be.”
Course Project: Interpreting Published Engineering Research
In selecting projects for Numerical Analysis of Engineering Systems, I decided to take a different approach. My goal was to encourage the students to get involved in engineering research and to possibly pursue postgraduate studies. I selected six published research papers that introduce an exact solution to an engineering problem related to smart materials and structures, including piezoelectric materials and shape memory alloys. These are the papers I selected:
- Birman V. (1999). “Analysis of an infinite shape memory alloy plate with a circular hole subjected to biaxial tension,” International Journal of Solids and Structures, vol. 36, pp. 167-178.
- Eshghinejad A.; Elahinia, M. (2015). “Exact solution for bending of shape memory alloy beams,” Mechanics of Advanced Materials and Structures, vol. 22, pp. 829–838.
- Vel, S.S.; Batra, R. C. (2001). “Exact solution for rectangular sandwich plates with embedded piezoelectric shear actuators,” AIAA JOURNAL, vol. 39, no. 7, pp. 1363 – 1373.
- Gaudenzi, P. (1998). “Exact higher order solutions for a simple adaptive structure,” International Journal of Solids and Structures, vol. 35, nos. 26-27, pp. 3595-3610.
- Nilanjan M.; M.C. Ray (2004). “Exact solutions for the analysis of piezoelectric fiber reinforced composites as distributed actuators for smart composite plates,” International Journal of Mechanics and Materials in Design, vol. 1, pp. 347–364.
- Pan, E. (2001). “Exact Solution for Simply Supported and Multilayered Magneto-Electro-Elastic Plates,” Journal of Applied Mechanics, vol. 68, pp. 608-618.
The authors of these papers provided an overview of a specific topic along with the main governing equations, mathematical formulation, and closed-form or semi-closed-form expressions for the problem solution; they then provided plots and graphs to illustrate their solutions. The students worked in teams. Each team was asked to select a paper, identify the key equations, and then write MATLAB code based on these equations to replicate the figures and plots in the paper. Each team was also asked to give a final presentation on their selected topic, their coding efforts, the results that the paper presented, the plots they were able to regenerate, and some conclusions.
This was the first time that many students had read a research paper. Some teams had trouble understanding the language and notations. For example, the use of subscripts and superscripts (indicial notation) raised several questions, but I held three guiding sessions to help them understand the technical and mathematical language used in these research papers. Despite these challenges, about half the teams successfully replicated the plots and graphs in their papers. Even those who found their paper too complex benefited from the experience of developing MATLAB code based on published research on an interesting topic new to them.
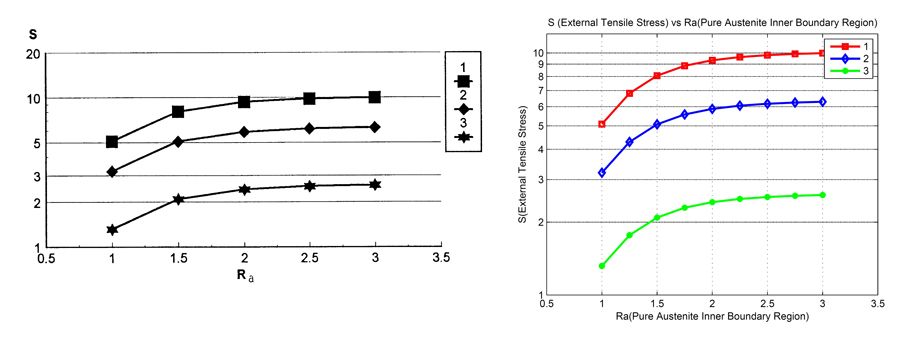
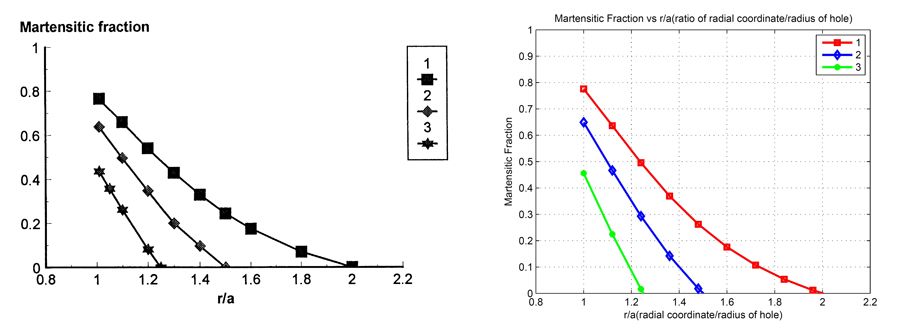
Figure 3 and Figure 4 show plots reported in Birman (1999) and the same plots that the students generated using their MATLAB code by implementing the closed-form solutions presented in this paper.
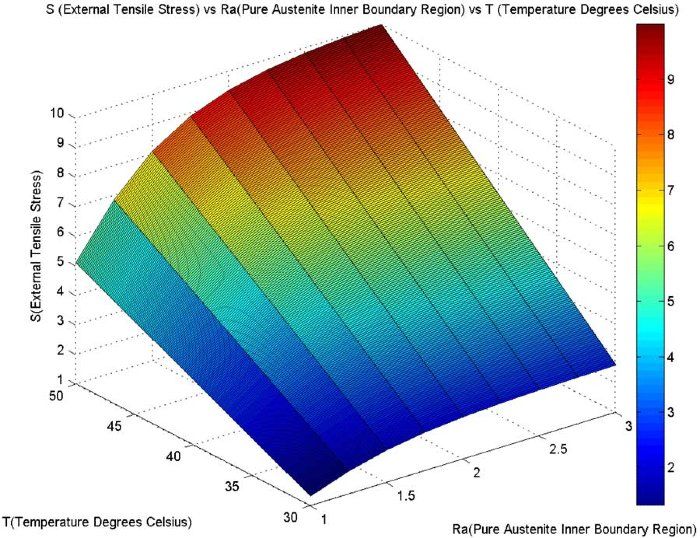
The team that worked on this project extended the plot in Figure 3 to consider a larger range of temperatures, and then created a 3D representation shown in Figure 5. This 3D plot was not presented in the research paper; it was created by the students as another way of displaying the relationship between the three parameters (Ra, S, and T) in the 3D space for a continuous range of temperature (T).
Supporting the Learning Pyramid
I strongly believe in the progression of student retention rates outlined in the learning pyramid—namely, that retention increases steadily with the following activities: listening to a lecture, reading, watching a video, watching a demonstration, participating in a discussion, practicing, and teaching the material to others. The final projects for my courses are designed to support the last two stages of this progression: practicing and teaching others. In developing a MATLAB application, or writing scripts to regenerate plots in a published research paper based on a sequence of equations, the students put into practice the programming and engineering concepts that they have learned. Likewise, in presenting their work to their classmates, or preparing a user manual for their developed apps, the students must effectively teach others what they have done as they explain how their MATLAB code works.
Published 2017 - 93083v00