Introduction to OFDM
Orthogonal Frequency Division Multiplexing (OFDM) enables high data rate transmissions by dividing modulated high bandwidth signal carriers onto many modulated narrowband subcarriers. For OFDM transmissions, the use of narrowband subcarriers reduces sensitivity to frequency selective fading. Many of the latest wireless and telecommunications standards use the multicarrier OFDM modulation format. Support of high data rates in single-carrier systems requires a wide bandwidth carrier, and consequently short symbol durations. Filtering a wide bandwidth carrier through a frequency selective multipath channel severely degrades the signal because the channel impulse response spans multiple symbols in time and makes the signal vulnerable to intersymbol interference (ISI).
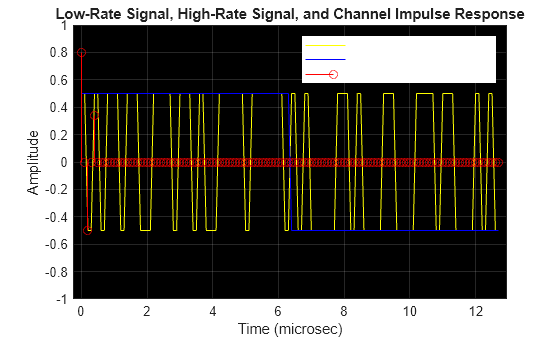
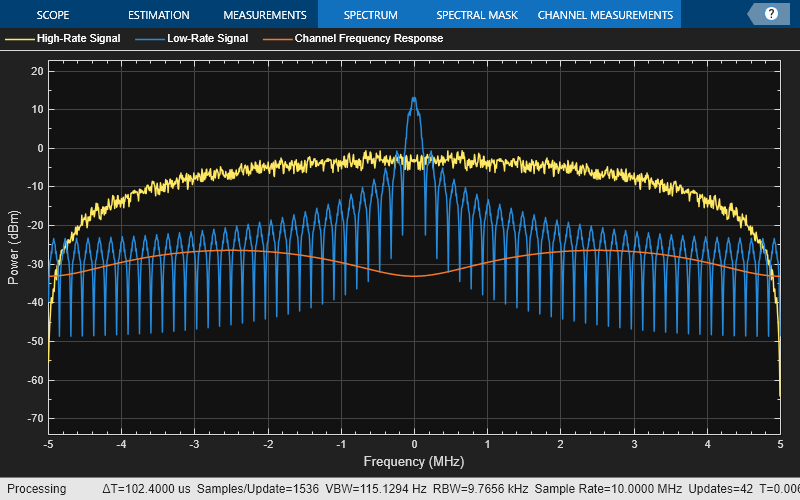
These time domain and frequency domain plots show a low-rate signal, a high-rate signal, and a frequency selective multipath channel response. The time domain plot shows the channel impulse response is easily contained in one symbol of the low-rate signal, but it extends across multiple symbols of the high-rate signal. The frequency domain plot shows that the channel magnitude is very flat across the passband of the low-rate signal, but varies considerably across the passband of the high-rate signal and causes ISI.
sa = helperPlotMultipath;
To avoid ISI while transmitting many parallel low bandwidth signals, the individual subcarriers must be orthogonal to each other. Avoiding ISI by transmitting many orthogonal low bandwidth subcarriers motivates OFDM. An OFDM modulator converts a high-rate serial stream of symbols into many parallel low-rate streams. Each orthogonal low-rate stream encounters a relatively flat channel with minimal ISI, and can be easily equalized.
To demonstrate, consider a pulse of duration , a symbol data rate , and additional pulses translated in frequency by , 2, and 3. The frequency-translated pulses are called subcarriers. These plots display the subcarriers in the time and frequency domains.
helperPlotOFDM

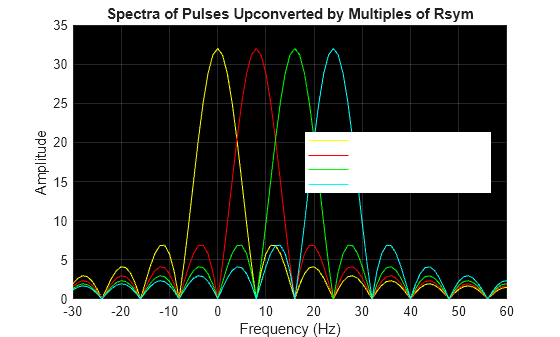
The frequency domain plot shows the orthogonal frequency translated pulses with spectral peaks of each subcarrier occurring at the zero crossings of all the other pulses.
An OFDM modulator sums all these subcarriers together to form its output signal. Here, the subcarriers are baseband modulated using the QAM-method. Mathematically, the sampled modulator output signal is given by
where
is a QAM-modulated symbol of the th subcarrier in the th OFDM time symbol
is the symbol rate of each of the low-rate QAM streams
is the number of subcarriers, or low-rate QAM streams
This equation simplifies to
which is a scaled version of the inverse discrete Fourier transform (IDFT) of the QAM symbol stream .
See Also
Functions
fft|ifft|ofdmmod|ofdmdemod|nrOFDMModulate(5G Toolbox) |nrOFDMDemodulate(5G Toolbox) |lteOFDMModulate(LTE Toolbox) |lteOFDMDemodulate(LTE Toolbox) |wlanWaveformGenerator(WLAN Toolbox)