Design an LQG Regulator
As an example of LQG design, consider the following regulation problem.

The goal is to regulate the plant output y around zero. The input disturbance d is low frequency with power spectral density (PSD) concentrated below 10 rad/s. For LQG design purposes, it is modeled as white noise driving a lowpass filter with a cutoff at 10 rad/s, shown in the following figure.
![]()
For simplicity, this noise is modeled as Gaussian white noise with variance of 1.
The following figure shows the Bode magnitude of the shaping filter.
Bode Magnitude of the Lowpass Filter

There is some measurement noise n, with noise intensity given by
Use the cost function
to specify the tradeoff between regulation performance and cost of control. The following equations represent an open-loop state-space model:
where (A,B,C) is a state-space realization of .
The following commands design the optimal LQG regulator F(s) for this problem:
sys = ss(tf(100,[1 1 100])) % State-space plant model % Design LQ-optimal gain K K = lqry(sys,10,1) % u = -Kx minimizes J(u) % Separate control input u and disturbance input d P = sys(:,[1 1]); % input [u;d], output y % Design Kalman state estimator Kest. Kest = kalman(P,1,0.01) % Form LQG regulator = LQ gain + Kalman filter. F = lqgreg(Kest,K)
These commands returns a state-space model F of the LQG regulator
F(s). The lqry,
kalman, and lqgreg functions perform discrete-time LQG
design when you apply them to discrete plants.
To validate the design, close the loop with feedback, create and add
the lowpass filter in series with the closed-loop system, and compare the open- and
closed-loop impulse responses by using the impulse function.
% Close loop
clsys = feedback(sys,F,+1)
% Note positive feedback.
% Create the lowpass filter and add it in series with clsys.
s = tf('s');
lpf= 10/(s+10) ;
clsys_fin = lpf*clsys;
% Open- vs. closed-loop impulse responses
impulse(sys,'r--',clsys_fin,'b-')
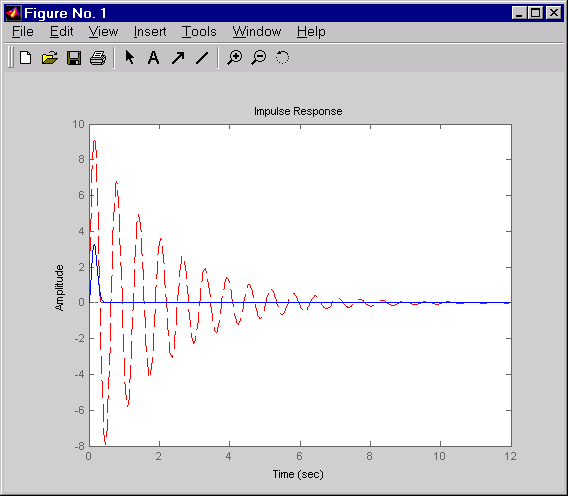
These commands produce the following figure, which compares the open- and closed-loop impulse responses for this example.
Comparison of Open- and Closed-Loop Impulse Response