getLoopTransfer
Open-loop transfer function of control system represented by
genss model
Syntax
Description
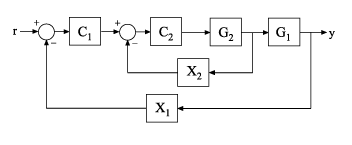
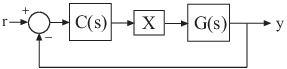
L = getLoopTransfer(T,Locations)T, containing the analysis points specified
by Locations. The point-to-point open-loop transfer function is
the response obtained by opening the loop at the specified locations, injecting
signals at those locations, and measuring the return signals at the same locations.
Examples
Input Arguments
Output Arguments
Tips
You can use
getLoopTransferto extract open-loop responses given a generalized model of the overall control system. This is useful, for example, for validating open-loop responses of a control system that you tune with the a tuning command such assystune.getLoopTransferis thegenssequivalent to the Simulink® Control Design™ commandgetLoopTransfer(Simulink Control Design), which works with theslTunerandslLinearizerinterfaces. Use the Simulink Control Design command when your control system is modeled in Simulink.
Version History
Introduced in R2012b
See Also
AnalysisPoint | getPoints | genss | getIOTransfer | systune | getLoopTransfer (Simulink Control Design)