Adaptive Filters
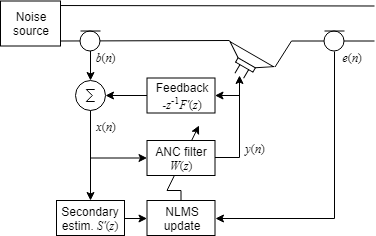
DSP System Toolbox™ offers several variations of the LMS and RLS adaptive finite impulse response (FIR) filter algorithms. While these algorithms differ in detail, they share a common operational approach, which is to minimize the error difference between the adaptive filter output and the desired signal. The mean square error (MSE) is the most commonly used metric to quantify this error. Adaptive filters are widely used in multiple applications including acoustic noise cancellation, echo cancellation, beam forming, system identification, bio medical signal enhancement, equalization of communication channels, etc. For examples illustrating some of these applications, see System Identification of FIR Filter Using LMS Algorithm, Noise Cancellation Using Sign-Data LMS Algorithm, and Inverse System Identification Using RLS Algorithm.
When the inputs are colored, the affine projection adaptive filter
algorithms offered by dsp.AffineProjectionFilter
object significantly improve the convergence speed over the LMS
variations. For increased computational cost, adaptive lattice filter
algorithm offered by dsp.AdaptiveLatticeFilter
object can provide a better convergence over the LMS and RLS
counterparts. You can also implement an adaptive FIR filter in the
frequency domain using the dsp.FrequencyDomainAdaptiveFilter object.
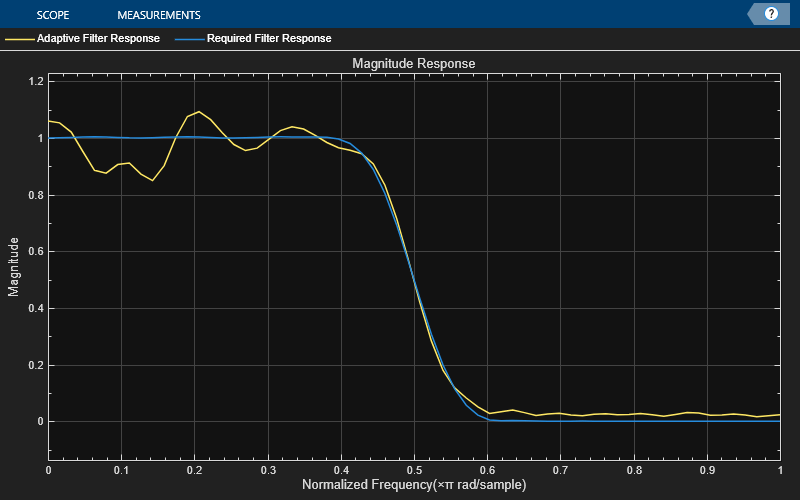
The convergence performance is determined by the trajectory of the
actual MSE, determined by msesim, and how it converges with the predicted MSE,
determined by msepred.
Objects
dsp.BlockLMSFilter | Compute output, error, and weights using block least mean squares (LMS) adaptive algorithm |
dsp.LMSFilter | Compute output, error, and weights of least mean squares (LMS) adaptive filter |
dsp.RLSFilter | Compute output, error and coefficients using recursive least squares (RLS) algorithm |
dsp.AffineProjectionFilter | Compute output, error and coefficients using affine projection (AP) Algorithm |
dsp.AdaptiveLatticeFilter | Adaptive lattice filter |
dsp.FastTransversalFilter | Fast transversal least-squares FIR adaptive filter |
dsp.FilteredXLMSFilter | Filtered XLMS filter |
dsp.FrequencyDomainAdaptiveFilter | Compute output, error, and coefficients using frequency-domain FIR adaptive filter |
Blocks
| Block LMS Filter | Compute output, error, and weights using LMS adaptive algorithm |
| Fast Block LMS Filter | Compute output, error, and weights using least mean squares (LMS) adaptive algorithm |
| Frequency-Domain Adaptive Filter | Compute output, error, and coefficients using frequency domain FIR adaptive filter |
| Kalman Filter | Predict or estimate states of dynamic systems |
| LMS Filter | Compute output, error, and weights using least mean squares (LMS) adaptive algorithm |
| LMS Update | Estimate weights of least mean squares (LMS) adaptive filter |
| RLS Filter | Compute filtered output, filter error, and filter weights for given input and desired signal using RLS adaptive filter algorithm |
Topics
- Overview of Adaptive Filters and Applications
General discussion on how adaptive filters work, list of adaptive filter algorithms in DSP System Toolbox, convergence performance, and details on few common applications.
- System Identification of FIR Filter Using LMS Algorithm
Identify an unknown system using LMS algorithm.
- System Identification of FIR Filter Using Normalized LMS Algorithm
Identify an unknown system using normalized LMS algorithm.
- Compare Convergence Performance Between LMS Algorithm and Normalized LMS Algorithm
Compare the speed with which the adaptive filter algorithms converge.
- Signal Enhancement Using LMS and NLMS Algorithms
Introduces adaptive filters through a signal enhancement application.
- Noise Cancellation Using Sign-Data LMS Algorithm
Perform noise cancellation using sign-data LMS algorithm.
- System Identification Using RLS Adaptive Filtering
This example shows how to use a recursive least-squares (RLS) filter to identify an unknown system modeled with a lowpass FIR filter.
- Inverse System Identification Using RLS Algorithm
Perform inverse system identification using dsp.RLSFilter.
- Compare RLS and LMS Adaptive Filter Algorithms
Comparison of RLS and LMS adaptive filter algorithms.
- Adapt Multiple Filters Using LMS Update Block
Adapt multiple filters independently using the same LMS Update block. Use the Adapt port of the LMS Update block to selectively enable or disable the filters from being adapted.
- Model Adaptive Linear Combiner using LMS Update Block
Use LMS Update block as an adaptive linear combiner.
- Remove Low Frequency Noise in Simulink Using Normalized LMS Adaptive Filter
Design a normalized LMS adaptive filter and use it to remove low frequency noise in Simulink®.
- Noise Cancellation in Simulink Using Normalized LMS Adaptive Filter
Remove colored noise generated from an acoustic environment, using a normalized LMS adaptive filter.
- Variable-Size Signal Support DSP System Objects
List of System objects that support variable-sized signals in DSP System Toolbox.