freqzmr
Compute DTFT approximation of impulse response of multirate or single-rate filter
Since R2024a
Description
[
outputs the impulse response discrete-time Fourier transform (DTFT) and corresponding
frequencies of the filter object specified in Y,Fout] = freqzmr(filtObj)filtObj.
If the input filter is a single-rate FIR or IIR filter, the behavior of
freqzmr and freqz functions is equivalent. If the filter is an irreducible multirate
filter, use the freqzmr function to analyze the frequency response of
the filter. For more details on the differences between these two functions, see Comparison of freqzmr and freqz functions. For more information on
reducible and irreducible multirate filters, see Overview of Multirate Filters.
freqzmr( plots the magnitude and phase
of the impulse response DTFT. The function also color-codes the distortion caused by the
rate changes. For more information on distortion, see Output Distortion.filtObj)
Examples
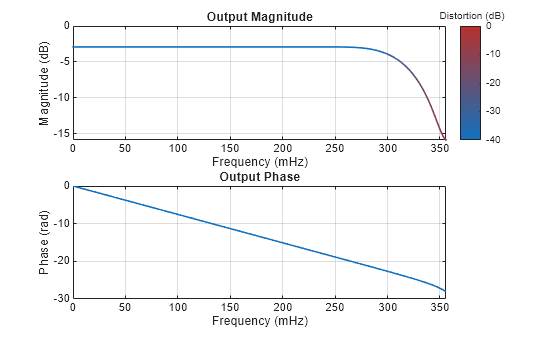
Compute and plot the impulse response DTFT of FIR rate converter using the freqzmr function.
firRC = dsp.FIRRateConverter(5,7); freqzmr(firRC)
Compute the impulse response DTFT of sample rate converter using the freqzmr function.
SRC = dsp.SampleRateConverter(InputSampleRate=77,... OutputSampleRate=32*24,... Bandwidth=23,... StopbandAttenuation=120); [Y,F] = freqzmr(SRC,MinimumFFTLength=1024);
When you do not specify any output arguments, the function plots the impulse response DTFT on a convenience plot.
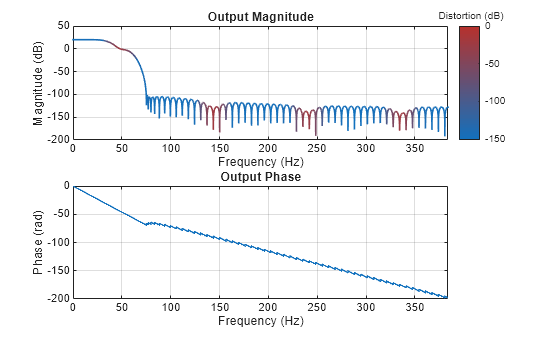
Plot the impulse response DTFT with maximum distortion sensitivity. In the red regions in the plot, you can expect some distortion due to the rate-conversion aliasing.
freqzmr(SRC,MinimumFFTLength=1024,DistortionThreshold=-inf);
To hide distortion coloring, set DistortionThreshold to 0.
freqzmr(SRC,MinimumFFTLength=1024,DistortionThreshold=0);

Specify the frequency range to be "centered".
freqzmr(SRC,MinimumFFTLength=1024,DistortionThreshold=-inf,FrequencyRange="centered");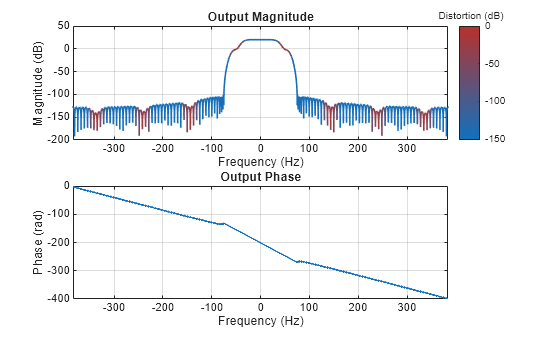
To compare, pass a random white noise signal to the sample rate converter. View the spectrum of the corresponding output in the spectrum analyzer.
You can see that the impulse response DTFT that freqzmr function computes is exactly the same as the spectrum of the output signal when you input a random white noise signal.
sa = spectrumAnalyzer(SampleRate=SRC.OutputSampleRate,PlotAsTwoSidedSpectrum=true,YLimits=[-200 20]); for k=1:10 u = randn(4096,1); y = SRC(u); sa(y); end

Design a composite filter that is a cascade of these filters:
Single-rate filter
Parallel structure of multirate filters
Design the single-rate filter using the dsp.LowpassFilter object in its default configuration.
singleRateFilter = dsp.LowpassFilter
singleRateFilter =
dsp.LowpassFilter with properties:
FilterType: 'FIR'
DesignForMinimumOrder: true
PassbandFrequency: 8000
StopbandFrequency: 12000
PassbandRipple: 0.1000
StopbandAttenuation: 80
NormalizedFrequency: false
SampleRate: 44100
Show all properties
The parallel structure contains a cascade of dsp.FIRInterpolator and dsp.FIRDecimator objects and a dsp.FIRRateConverter object.
Design the dsp.FIRInterpolator and the dsp.FIRRateConverter objects using the designBandpassFIR function.
B1 = 2.5*designBandpassFIR(FilterOrder=256,... CenterFrequency=0.3,Bandwidth=1/5); B2 = 0.25*designBandpassFIR(FilterOrder=256,... CenterFrequency=0.7,Bandwidth=1/20);
Create a parallel structure of multirate filters using the parallel and cascade functions.
multirateFilter = parallel(cascade(dsp.FIRInterpolator(5,B1),...
dsp.FIRDecimator(2)),dsp.FIRRateConverter(10,4,B2))multirateFilter =
dsp.ParallelFilter with properties:
Branch1: [1×1 dsp.FilterCascade]
Branch2: [1×1 dsp.FIRRateConverter]
CloneBranches: true
Create a composite filter that is a cascade of the single-rate filter and the parallel filter.
compositeFilter = cascade(singleRateFilter,multirateFilter)
compositeFilter =
dsp.FilterCascade with properties:
Stage1: [1×1 dsp.LowpassFilter]
Stage2: [1×1 dsp.ParallelFilter]
CloneStages: true
Compute and plot the impulse response DTFT of this filter using the freqzmr function. Set MinimumFFTLength to 512. Set the frequency range to be "centered".
freqzmr(compositeFilter,MinimumFFTLength=512,FrequencyRange='centered')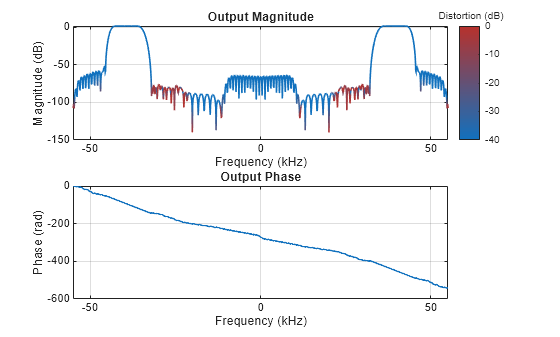
Input Arguments
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: src =
dsp.SampleRateConverter(InputSampleRate=77,OutputSampleRate=32*24,Bandwidth=23,StopbandAttenuation=120);
[Y,Fout] =
freqzmr(src,MinimumFFTLength=1024,DistortionThreshold=-inf);
Shortest discrete spectrum length, specified as a positive integer. When the
function resamples the spectrum internally (for example, during downsampling), the
size of the resampled spectrum is no shorter than
MinimumFFTLength. For more information, see DTFT of Downsampled Signal.
Data Types: double
Sample rate of the input signal FsIn in Hz, specified as a positive integer.
If you do not specify the input sample rate, the function inherits this value from the filter object. If the input filter object contains an explicit property to specify the input sample rate, the function uses the value of that property. If the filter object does not contain any such property, the function uses a value of 1.
Data Types: double
Frequency range of the DTFT, specified as one of these:
"auto"–– The function automatically determines the appropriate choice ("onesided"or"twosided") based on the system symmetry. The function selects"onesided"when the system spectrum is Hermitian symmetric and"twosided"otherwise."onesided"–– Impulse response DTFT contains only the positive frequencies. Frequency range is [0 Fsout/2]."twosided"–– Frequency range is [0 Fsout]."centered"–– Frequency range is [−Fsout/2 Fsout/2].
Fsout is the output sample rate and is given by the equation Fsout = FsIn×(L/M), where L/M is the rate conversion ratio of the input filter object.
Distortion threshold in dB to determine ambiguity in the convenience magnitude
plot, specified as a scalar in the range (−∞ 0]. The
DistortionThreshold argument is the threshold over which the
signal is considered ambiguous.
Decrease the threshold value for a more sensitive detection of distortion. The function colors the convenience magnitude plot according to the distortion ratio. Red indicates maximum distortion (two or more branches have the same power), while blue indicates no distortion. If the distortion threshold is 0 dB, the function hides all distortion coloring.
The function ignores any distortion value below the value of
DistortionThreshold and treats the output as
non-ambiguous.
Here is a plot of the impulse response DTFT of an FIR rate converter with the distortion threshold of −∞. This plot shows the most sensitive detection of distortion.

Increase the threshold value to −40 dB. The function ignores all distortions below −40 dB.
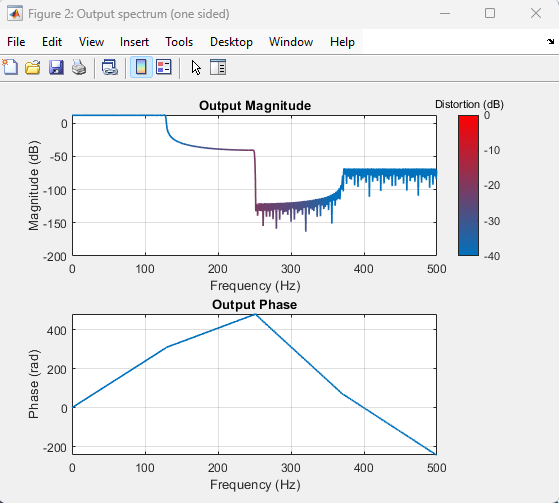
Increasing the threshold value to 0 dB shows no distortion on the plot because the function ignores all the distortion values.
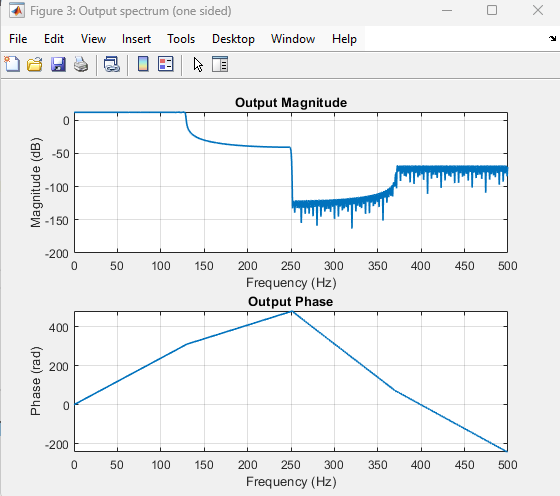
For more information, see Output Distortion.
Data Types: double
Output Arguments
DTFT approximation of the impulse response, returned as a column vector. The length
of the impulse response DTFT depends on the MinimumFFTLength value
and the rate conversion factors of the multirate filter stages.
Data Types: double
Complex Number Support: Yes
Output frequencies in Hz corresponding to the impulse response DTFT approximation,
returned as a column vector. The length of Fout equals the length
of Y. The range of Fout depends on the
FrequencyRange.
Data Types: double
More About
The discrete-time Fourier transform (DTFT) of a sequence x[m] sampled at rate T is a periodic complex-valued function and is given by
, where T is the sample rate of the signal. DTFT plays a central role in the analysis of discrete signals and systems.
For computational purposes, DTFT is sampled on a finite set of frequencies and can be expressed in terms of DFT and FFT.
The freqz function plots the frequency response of
a single-rate FIR or IIR filter, while the freqzmr function plots the
DTFT approximation of the filter impulse response. This distinction stems from the fact that
multirate filters, in general, do not have a frequency response because a single input tone
can generate multiple output tones. The freqzmr function accounts for
multirate operations in its DTFT approximation, while freqz assumes
that the filter is a single-rate FIR or IIR filter.
Here are a few examples which illustrate the behavior of freqz and
freqzmr for single-rate filters and various types of multirate
filters.
Single-Rate Filters
For single-rate FIR or IIR filters, the frequency response is equal to the DTFT of their
impulse response, and the behavior of freqzmr and
freqz functions is equivalent.
Consider the dsp.LowpassFilter object which is a single-rate
filter.
lpFilter = dsp.LowpassFilter
Plot the frequency response of this filter using freqz and the DTFT
of the impulse response using freqzmr. Overlay the two plots.
The two plots are exactly the same.

Multirate Filters
Multirate filters cannot be characterized by a single transfer function and do not have a frequency response in the usual sense. However, multirate filters have a well-defined impulse response, whose DTFT gives valuable information about the spectral content of their outputs.
The freqzmr function computes the DTFT approximation of the
multirate filter impulse response and accounts for multirate operations while doing so. This
behavior allows the freqzmr function to capture multirate effects such
as imaging and aliasing, while the freqz function does not capture
those effects.
This filter is an antialiasing FIR filter with a downsample factor of 4.
firDec = dsp.FIRDecimator(4)
The freqz function inspects this filter as a single-rate filter.
The freqzmr function computes the DTFT approximation of the filter
impulse response. The DTFT plot accounts for aliasing and looks different compared to the
frequency response plot. The aliased components compensate to a flat response. The plot
shows these components by coloring them in red. For more information, see Output Distortion.

Multirate filters can be reducible or irreducible. A multirate filter is said to be
reducible if it can be modified through noble identities to produce a single-rate FIR or IIR
filter, as firDec in the previous example. For more information, see Overview of Multirate Filters. If the
input filter is a reducible multirate filter, you can use the freqz
function to analyze the filter. The function analyzes the equivalent FIR or IIR stage and
treats the filter as a single-rate FIR or IIR filter.
Multirate Filter Reducing to a Single-Stage Filter
Consider this FIR rate converter which is trivially reducible for it has a single FIR stage.
firrc = dsp.FIRRateConverter(3,2,triang(9))
firrc =
dsp.FIRRateConverter with properties:
Main
InterpolationFactor: 3
DecimationFactor: 2
NumeratorSource: 'Property'
Numerator: [9×1 double]
With an input sample rate of 1 kHz, the output sample rate is 1.5 kHz. Plot the
frequency response of the filter using freqz, and the DTFT of the
filter impulse response using freqzmr. You can see that there is
distortion in the frequency range [0.4 0.75 kHz]. The DTFT plot shows this
distortion.

Consider this filter that is a cascade of a lowpass filter and an FIR rate converter. You can reduce this filter to a single stage.
lpfilt = dsp.LowpassFilter(SampleRate=1e3,... PassbandFrequency=80,StopbandFrequency=100,FilterType='IIR'); firrc = dsp.FIRRateConverter(3,4); cascFilt = cascade(lpfilt,firrc)
cascFilt =
dsp.FilterCascade with properties:
Stage1: [1×1 dsp.LowpassFilter]
Stage2: [1×1 dsp.FIRRateConverter]
CloneStages: true
Plot the frequency response of this filter using freqz and the DTFT
of the filter impulse response using freqzmr. Overlay and compare the
two plots.
The two functions generate plots that look similar but are not the same. The
freqzmr plot shows the distortion regions in red, where there is
rate-conversion aliasing.
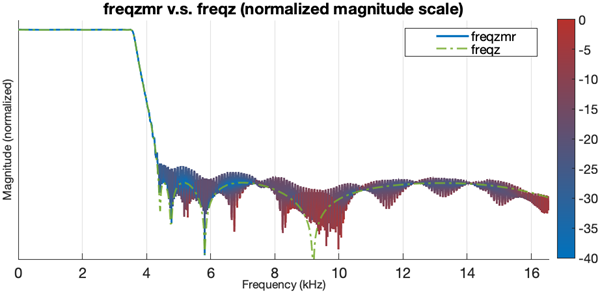
Irreducible Multirate Filter
Lastly, if the input filter is an irreducible multirate filter, use the
freqzmr function to analyze the filter in the frequency domain. For
more information on irreducible filters, see Overview of Multirate Filters.
Consider this filter that is a cascade of two FIR rate converters. This filter is irreducible.
firrc1 = dsp.FIRRateConverter; firrc2 = dsp.FIRRateConverter(3,4); cascFilt = cascade(firrc1,firrc2)
cascFilt =
dsp.FilterCascade with properties:
Stage1: [1×1 dsp.FIRRateConverter]
Stage2: [1×1 dsp.FIRRateConverter]
CloneStages: true
When you try to analyze this filter with freqz, the function errors
out.
To analyze this filter, use the freqzmr function, which in its
default configuration shows the DTFT of the filter impulse response.
freqzmr(src)
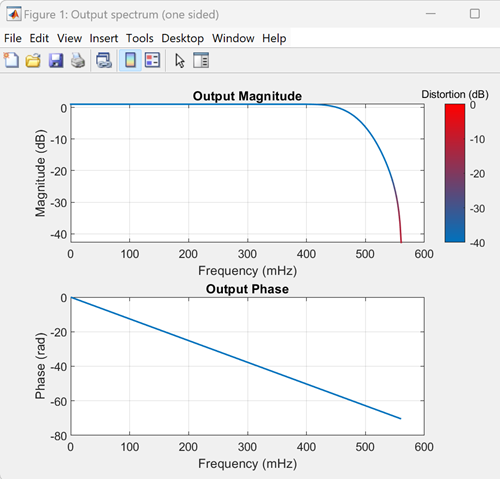
To summarize, for irreducible multirate filters, use the freqzmr
function. For single-rate FIR or IIR filters, the behavior of freqz and
freqzmr is equivalent.
Here is a table that compares the two functions and lists the key differences.
freqzmr | freqz | |
|---|---|---|
| Computation | DTFT approximation of filter impulse response h DTFT(h) | Frequency response of the filter, which is the transfer function evaluated on the unit circle |
| Single-rate convolution filters | ✓ | ✓ |
| Reducible multirate filters | ✓ | ✓ Performs analysis on the single-rate FIR or IIR
equivalent. The plot looks different compared to the
|
| Irreducible multirate filters | ✓ | ╳ |
| Captures multirate effects such as imaging an aliasing | ✓ | ╳ |
| Support for normalized frequencies | ╳ | ✓ |
Algorithms
The freqzmr algorithm treats the input filter object as a combination
of FIR or IIR (single-rate) filters and multirate operations (upsample and downsample). The
function processes the DTFT through each stage consecutively. For more information on DTFT,
see Discrete-Time Fourier Transform (DTFT) and DFT and FFT.
Here is the block diagram of a single-rate filter with an input sequence x[m] and an output sequence y[m].
![]()
where h is the impulse response of the single-rate filter.
The freqzmr function computes the impulse response DTFT, that is,
DTFT(h).
![]()
For a given input signal x[m], the output of the downsampling operation is given by y[n] = x[Mm].
The DTFT of the downsampled signal is periodic and its period 1/(MT) is 1/M of the period of X1/T.
For multirate filters, the components in can overlap and interfere with each other resulting in aliasing. To resolve aliasing, it is important that one of the components dominates the rest in its value. This component contributes to the sum while the rest are 0 and resolves the issue of aliasing. In most cases, this component corresponds to m=0 (baseband component), that is, Y(1/MT)(f)≅X1/T(f/M).
Multirate distortion is the level of ambiguity between these components. You can specify
the threshold in dB over which the function considers the signal ambiguous using the
DistortionThreshold property. For more information, see Output Distortion.
Computing the DTFT of Downsampled Signal
DTFT downsampling is done through reshaping of the DTFT samples vector and taking a sum across columns. To downsample a signal with DTFT samples vector X by a decimation factor M, the downsampled DTFT is:
NX = size(X,1); Y = (1/M)*sum(reshape(X,NX/M,M),2);
The DTFT array X is usually resampled at a higher frequency
resolution (increase by NX) prior to reshaping. This is done in order to
make the NX length divisible by M and to ensure that
the resolution of the downsampled DTFT Y is no less than
MinimumFFTLength.
![]()
For a given input signal x[m], the output of the upsampling operation is given by
.
y[n] operates at a rate L/T. The DTFT of the upsampled signal y is identical to the DTFT of x, that is, YL/T(f) = X1/T(f). The only difference is in the period, which is L/T, that is, L times larger on the frequency domain.
The freqzmr function determines the DTFT of the upsampled signal by
replicating the input DTFT samples vector L times.
function Y = upsampleDTFT(X,L) Y = repmat(X,L,1); end
Cascade Filters
![]()
For a cascade of filters, the freqzmr function computes the output
DTFT by passing the output DTFT of each stage as the input DTFT of the following stage. The
first stage input is an impulse.
freqzmr(cascade(H1,H2)) = freqzmr(H2,...
InputSpectrum=freqzmr(H1))If you have multiple stages in the cascade, the freqzmr function
computes the impulse response DTFT using this
logic.
function Y = cascadeDTFT(obj,X,MinimumFFTLength) Y = X; for k = 1:NumStages Y = outputDTFT(Stage(k),Y,MinimumFFTLength); end end
Parallel Filters

For parallel filters, the DTFT output is a sum of the DTFTs of the filter outputs on the individual branches.
In multirate systems, an input frequency generates several output frequencies due to aliasing and imaging. As a result, an output frequency component is often a combination of several different frequency components.
You can express the output DTFT of a multirate filter as a sum of the components Q0, Q1, …., QM-1.
where:
M is the total decimation factor.
Q0, Q1, …., QM-1 are DTFT components that the function computes through rate change operations.
Ideally, only one branch contributes to the sum while the rest are 0 (no aliasing), that is, Qm = 0 for all m except for one. As soon as more than one of the branches has a nonzero value, Y(f) exhibits aliasing.
The distortion is the level of ambiguity of the frequency branches Qm(f) in the sum above. It is defined as the inverse power ratio between the dominant component and the average power of the remaining components.
The distortion ratio ranges between 0 and 1 (or −∞ to 0 in dB), where higher values indicate more ambiguity. A 1:1 ratio (0 dB) indicates that there is no dominant component, and the signal is totally ambiguous. In contrast, a 0-ratio (−∞ dB) indicates that the output frequency is non-ambiguous.
The freqzmr function sorts
m1, ….,
mM at every frequency according to the
corresponding Qm magnitude values. The distortion
ratio is invariant under permutations, that is, changing the order of the branches does not
alter the distortion. The distortion ratio is a real number between 0 and 1. These values
indicate where aliasing is present in a multirate system.
The function colors the impulse response DTFT depending on the value of the distortion
ratio. Red indicates maximum distortion (two or more branches have the same power), while
blue indicates no distortion. The function ignores any distortion value below the value
specified in DistortionThreshold.
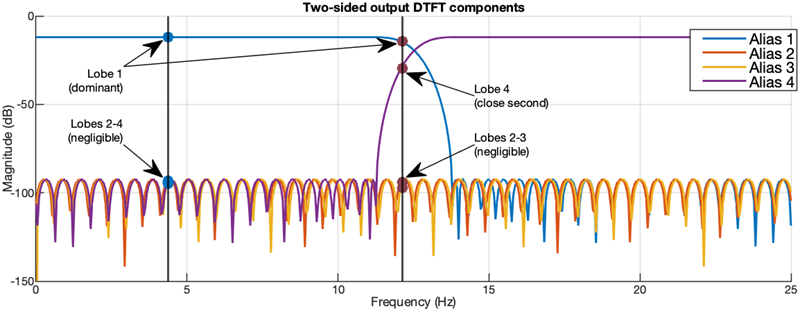
The following figure shows the distortion ratio in two frequencies. In the lower
frequency (f = 4.375 Hz), there is a fairly low distortion since the
dominant lobe is about 80 dB above the rest of the lobes. In the higher frequency
(f = 12.125 Hz), there is far more significant interference as alias
lobe 4 is much closer to the dominant lobe 1. This is indicated by the red color on the
freqzmr plot.

Version History
Introduced in R2024aStarting in R2024b, the freqzmr analysis function supports the
dsp.VariableFIRDecimator and dsp.VariableFIRInterpolator objects.
Starting in R2024b, this function supports the dsp.DCBlocker object.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)