Levinson-Durbin
Solve linear system of equations using Levinson-Durbin recursion
Libraries:
DSP System Toolbox /
Estimation /
Linear Prediction /
Linear System Solvers
DSP System Toolbox /
Math Functions /
Matrices and Linear Algebra /
Linear System Solvers
Description
The Levinson-Durbin block solves the nth-order system of linear equations
Ra = b
in the cases where:
R is a Hermitian, positive-definite, Toeplitz matrix.
b is identical to the first column of R shifted by one element and with the opposite sign.
Examples
Analysis and Synthesis of Speech
A speech signal is usually represented in digital format, which is a sequence of binary bits. For storage and transmission applications, it is desirable to compress a signal by representing it with as few bits as possible, while maintaining its perceptual quality. Quantization is the process of representing a signal with a reduced level of precision. If you decrease the number of bits allocated for the quantization of your speech signal, the signal is distorted and the speech quality degrades.
Ports
Input
Specify the input to the block, r =
[r(1)
r(2) ...
r(n+1)] as a
vector or a matrix. If the input is a matrix, the block treats each
column as an independent channel and solves it separately. Each channel
of the input contains lags 0 through
n of an autocorrelation sequence, which appear in
the matrix R.
If the input is fixed point, it must be a signed integer or a signed fixed point value with a power-of-two slope and zero bias.
Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes
Output
Model coefficients A, returned as a vector or a matrix. A has the same dimension as the input.
For each channel, port A outputs
A = [1
a(2) a(3) ...
a(n+1)], the
solution to the Levinson-Durbin equation. You can also view the elements
of each output channel as the coefficients of an
nth-order autoregressive (AR) process.
Dependencies
To enable this port, set Output(s) to
A and K or
A.
Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes
Reflection coefficients K, returned as a vector or a matrix. K has the same dimension as the input, less one element.
For each channel, port K outputs
K =
[k(1)
k(2) ...
k(n)], which
contains n reflection coefficients.
A scalar input channel causes an error when you select
K. You can use reflection coefficients to realize
a lattice representation of the AR process. For more details, see Applications.
Dependencies
To enable this port, set Output(s) to
A and K or
K.
Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes
Output prediction error power P, returned as vector of length equal to the number of input channels. Each element in the vector is the prediction error power for each channel.
For each channel, P represents the power of the output of an FIR filter with taps A and input autocorrelation described by r, where A represents a prediction error filter and r is the input to the block. In this case, A is a whitening filter. P has one element per input channel.
Dependencies
To enable this port, select the Output prediction error power (P) check box.
Data Types: single | double | int8 | int16 | int32 | fixed point
Parameters
Main Tab
Specify the solution representation of Ra = b to output:
Polynomial coefficients (
A) –– For each channel, port A outputsA =[1 a(2) a(3) ... a(n+1)], the solution to the Levinson-Durbin equation. A has the same dimension as the input. You can also view the elements of each output channel as the coefficients of an nth-order autoregressive (AR) process.Reflection coefficients (
K) –– For each channel, port K outputsK =[k(1) k(2) ... k(n)], which contains n reflection coefficients and has the same dimension as the input, less one element. A scalar input channel causes an error when you selectK. You can use reflection coefficients to realize a lattice representation of the AR process described later in this page.Both model coefficients and reflection coefficients (
A and K) –– The block outputs both representations at their respective ports. A scalar input channel causes an error when you selectA and K.
When the input is a scalar or row vector, you must set this parameter
to A.
Select this parameter to output the prediction error power for each channel at port P.
When you select this check box and the first element of the input,
r(1), is zero, the block outputs the following
vectors, as appropriate:
A = [1 zeros(1,n)]K = [zeros(1,n)]P = 0
When you clear this check box, the block outputs a vector of NaNs for each channel
whose r(1) element is zero. In general, an input with
r(1) = 0 is invalid because it
does not construct a positive-definite matrix R.
Often, however, blocks receive zero-valued inputs at the start of a
simulation. The check box allows you to avoid propagating
NaNs during this period.
Data Types Tab
Note
Floating-point inheritance takes precedence over the data type settings defined on this pane. When inputs are floating point, the block ignores these settings, and all internal data types are floating point.
Specify the rounding mode for fixed-point operations as one of the following:
FloorCeilingConvergentNearestRoundSimplestZero
For more details, see rounding mode.
When you select this parameter, the block saturates the result of its
fixed-point operation. When you clear this parameter, the block wraps
the result of its fixed-point operation. For details on
saturate and wrap, see overflow
mode for fixed-point operations.
Specify the product output data type as Inherit: Same as
input or a numeric type. See Fixed-Point Data Types and Multiplication Data Types for illustrations depicting the
use of the product output data type in this block. You can set it
to:
A rule that inherits a data type, for example,
Inherit: Same as inputAn expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the Product
output parameter.
to display the Data Type
Assistant, which helps you set the Product
output parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Specify the accumulator data type as Inherit: Same as
input, Inherit: Same as product
output, or a numeric type. See Fixed-Point Data Types for
illustrations depicting the use of the accumulator data type in this
block. You can set it to:
A rule that inherits a data type, for example,
Inherit: Same as inputA rule that inherits a data type, for example,
Inherit: Same as product outputAn expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the
Accumulator parameter.
to display the Data Type
Assistant, which helps you set the
Accumulator parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Specify the polynomial coefficients (A) data type
as a numeric type. See Fixed-Point Data Types for
illustrations depicting the use of the A data type in this block. You
can set it to an expression that evaluates to a valid data type, for
example, fixdt(1,16,10).
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the A
parameter.
to display the Data Type
Assistant, which helps you set the A
parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Specify the reflection coefficients (K) data type
as a numeric type. See Fixed-Point Data Types for
illustrations depicting the use of the K data type in this block. You
can set it to an expression that evaluates to a valid data type, for
example, fixdt(1,16,10).
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the K
parameter.
to display the Data Type
Assistant, which helps you set the K
parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Specify the prediction error power (P) data type as
Inherit: Same as input or a numeric type.
See Fixed-Point Data Types for
illustrations depicting the use of the P data type in this block. You
can set it to:
A rule that inherits a data type, for example,
Inherit: Same as inputAn expression that evaluates to a valid data type, for example,
fixdt(1,16,0)
Click the Show data type assistant button
![]() to display the Data Type
Assistant, which helps you set the P
parameter.
to display the Data Type
Assistant, which helps you set the P
parameter.
See Specify Data Types Using Data Type Assistant (Simulink) for more information.
Specify the minimum values that the polynomial coefficients,
reflection coefficients, or prediction error power should have. The
default value is [] (unspecified). Simulink® uses this value to perform:
Parameter range checking (see Specify Minimum and Maximum Values for Block Parameters (Simulink))
Automatic scaling of fixed-point data types
Specify the maximum values that the polynomial coefficients,
reflection coefficients, or prediction error power should have. The
default value is [] (unspecified). Simulink uses this value to perform:
Parameter range checking (see Specify Minimum and Maximum Values for Block Parameters (Simulink))
Automatic scaling of fixed-point data types
Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
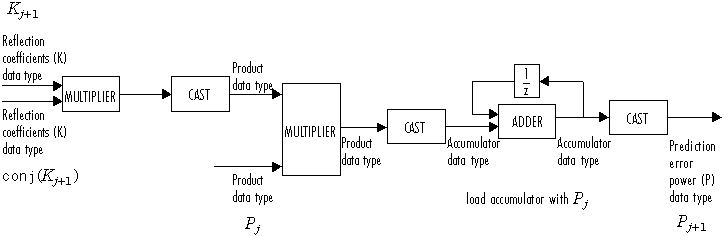
The diagrams in this section show the data types used within the Levinson-Durbin block for fixed-point signals.
After initialization the block performs n updates. At the (j+1) update,
The following diagram displays the fixed-point data types used in this calculation:

The block then updates the reflection coefficients K according to
The block then updates the prediction error power P according to
The next diagram displays the fixed-point data types used in this calculation:

The polynomial coefficients A are then updated according to
This diagram displays the fixed-point data types used in this calculation:
One application of the Levinson-Durbin formulation implemented by this block is in
the Yule-Walker AR problem, which concerns modeling an unknown system as an
autoregressive process. You would model such a process as the output of an all-pole
IIR filter with white Gaussian noise input. In the Yule-Walker problem, the use of
the signal's autocorrelation sequence to obtain an optimal estimate leads to an
Ra = b equation of the
type shown above, which is most efficiently solved by Levinson-Durbin recursion. In
this case, the input to the block represents the autocorrelation sequence, with
r(1) being the zero-lag value. The output at the block's A
port then contains the coefficients of the autoregressive process that optimally
models the system. The coefficients are ordered in descending powers of
z, and the AR process is minimum phase. The prediction error,
G, defines the gain for the unknown system, where :
The output at the block's K port contains the corresponding reflection
coefficients, [k(1)
k(2) ...
k(n)], for the lattice
realization of this IIR filter. The Yule-Walker AR Estimator block implements this
autocorrelation-based method for AR model estimation, while the Yule-Walker Method
block extends the method to spectral estimation.
Another common application of the Levinson-Durbin algorithm is in linear
predictive coding, which is concerned with finding the coefficients of a moving
average (MA) process (or FIR filter) that predicts the next value of a signal from the current
signal sample and a finite number of past samples. In this case, the input to the
block represents the signal's autocorrelation sequence, with
r(1) being the zero-lag value, and the
output at the block's A port contains the coefficients of the predictive MA process
(in descending powers of z).
These coefficients solve the following optimization problem:
Again, the output at the block's K port contains the corresponding reflection
coefficients, [k(1) k(2) ... k(n)], for the lattice realization
of this FIR filter. The Autocorrelation LPC block in the Linear
Prediction library implements this autocorrelation-based prediction method.
Algorithms
The algorithm requires O(n2) operations for each input channel. This implementation is therefore much more efficient for large n than standard Gaussian elimination, which requires O(n3) operations per channel.
References
[1] Golub, G. H. and C. F. Van Loan. Sect. 4.7 in Matrix Computations. 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.
[2] Ljung, L. System Identification: Theory for the User. Englewood Cliffs, NJ: Prentice Hall, 1987. Pgs. 278–280.
[3] Kay, Steven M. Modern Spectral Estimation: Theory and Application. Englewood Cliffs, NJ: Prentice Hall, 1988.
Extended Capabilities
Generated code relies on the memcpy or
memset function (string.h) under certain
conditions.
Version History
Introduced before R2006a
See Also
Functions
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)

