impulse

Generate univariate autoregressive integrated moving average (ARIMA) model impulse response function (IRF)

Syntax

impulse(Mdl)

impulse(Mdl,numObs)

y = impulse(___)

Description

impulse generates, or plots, the impulse response function (IRF) of a univariate autoregressive integrated moving average (ARIMA) process specified by an arima model object.

Alternatively, you can use armairf to generate or plot the IRF of an ARMA process specified by AR and MA lag operator polynomial coefficients.

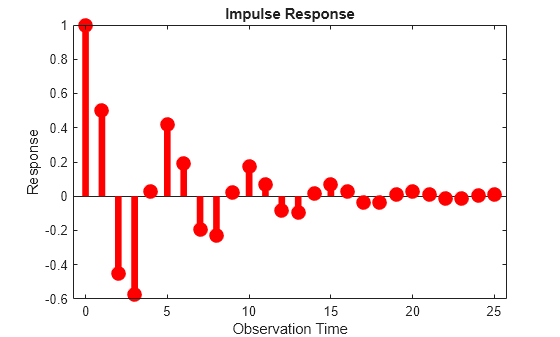
impulse(Mdl) plots a discrete stem plot of the IRF of the univariate ARIMA model Mdl to the current figure window. impulse plots the dynamic responses starting at period 0, during which impulse applies a unit shock to the innovation.

impulse(Mdl,numObs) plots the numObs dynamic responses from periods 0 through numObs – 1.

y = impulse(___) returns the IRF y of the ARIMA model, using any of the input argument combinations in the previous syntaxes.

Examples

Plot IRF of Known AR(2) Model

Create the AR(2) model

$$y_t=0.5y_{t-1}-0.7y_{t-2}+{\epsilon }_t,$$

where ${\epsilon }_{\mathit{t}}$ is a standard Gaussian process.

Mdl = arima('AR',{0.5,-0.7},'Constant',0)

Mdl = 
  arima with properties:

     Description: "ARIMA(2,0,0) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 2
               D: 0
               Q: 0
        Constant: 0
              AR: {0.5 -0.7} at lags [1 2]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: NaN

Plot the IRF of ${\mathit{y}}_{\mathit{t}}$.

impulse(Mdl)

The IRF has length 26; it begins at period 0, during which impulse applies a unit shock to the innovation, and ends at period 25. impulse computes the IRF by inverting the underlying AR lag operator polynomial. The length of the IRF is 26 because the dynamic multipliers beyond period 25 are below the division algorithm tolerances.

The model is stationary; the impulse response function decays with a sinusoidal pattern.

You can change characteristics of the plot by adjusting the properties of the underlying stem plot. The axes handle object stores the stem plot handle in the Children property.

Increase the line thickness (the default is 0.5). Also, change the color of the stem plot to red by using the RGB color value.

h = gca; % Current axes handle
stemh = h.Children;
stemh.LineWidth = 5;
stemh.Color = [1 0 0];

Specify Number of Periods in IRF

Load the quarterly US GDP data set.

load Data_GDP

For details on the data, enter Description at the command line.

Compute the GDP growth rate.

y = price2ret(Data);

Consider an ARMA(2,2) model for the GDP rate series. Create an arima model template for estimation.

Mdl = arima(2,0,2)

Mdl = 
  arima with properties:

     Description: "ARIMA(2,0,2) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 2
               D: 0
               Q: 2
        Constant: NaN
              AR: {NaN NaN} at lags [1 2]
             SAR: {}
              MA: {NaN NaN} at lags [1 2]
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: NaN

NaN values in properties are placeholders for estimable model parameters.

Fit the model to the entire series.

EstMdl = estimate(Mdl,y)

 
    ARIMA(2,0,2) Model (Gaussian Distribution):
 
                  Value       StandardError    TStatistic      PValue  
                __________    _____________    __________    __________

    Constant     0.0036702     0.00058179        6.3084      2.8185e-10
    AR{1}            1.372       0.089005        15.415      1.3049e-53
    AR{2}          -0.8069       0.069497       -11.611      3.6412e-31
    MA{1}          -1.1432        0.10159       -11.253       2.247e-29
    MA{2}          0.67355        0.08512        7.9129       2.515e-15
    Variance    8.3071e-05     5.9331e-06        14.001      1.5322e-44

EstMdl = 
  arima with properties:

     Description: "ARIMA(2,0,2) Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 2
               D: 0
               Q: 2
        Constant: 0.00367019
              AR: {1.37199 -0.806899} at lags [1 2]
             SAR: {}
              MA: {-1.14315 0.673547} at lags [1 2]
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: 8.30707e-05

The estimated AR(2) model of the GDP rate series is

$$y_t=0.004+1.372y_{t-1}-0.807y_{t-2}+{\epsilon }_t-1.143{\epsilon }_{t-1}+0.674{\epsilon }_{t-2},$$

where ${\epsilon }_{\mathit{t}}$ is a Gaussian series with mean 0 and variance 0.00008.

Compute the IRF of the estimated model for 50 periods.

impulse(EstMdl,50)

The dynamic response to the initial innovation shock dissipates after about 35 quarters.

Return IRF of Known ARMA(1,1) Model

Create the ARMA(1,1) model

$$y_t=0.7y_{t-1}+{\epsilon }_t+0.2{\epsilon }_{t-1}.$$

Mdl = arima('AR',0.7,'MA',0.2,'Constant',0);

Return the IRF for 15 periods.

numObs = 15;
periods = 0:(numObs-1);
y = impulse(Mdl,numObs);
irf = table(periods',y,'VariableNames',["Period" "y"])

irf=15×2 table
    Period       y    
    ______    ________

       0             1
       1           0.9
       2          0.63
       3         0.441
       4        0.3087
       5       0.21609
       6       0.15126
       7       0.10588
       8      0.074119
       9      0.051883
      10      0.036318
      11      0.025423
      12      0.017796
      13      0.012457
      14       0.00872

y(0), which is the dynamic response of the system at the time impulse shocks the innovation, is 1.

Input Arguments

Mdl — Fully specified ARIMA model

arima model object

Fully specified ARIMA model, specified as an arima model object created by arima or estimate.

The properties of Mdl cannot contain NaN values.

numObs — Number of periods to include in IRF

positive integer

Number of periods to include in the IRF (the number of periods for which impulse computes the IRF), specified as a positive integer.

If you specify numObs, impulse computes the IRF by filtering a unit impulse, followed by a vector of zeros of length numObs – 1, through the model Mdl. In this case, the filtering algorithm is efficient.

By default, impulse determines the length of the IRF by implementing the following algorithm:

1. Represent the ARIMA process as a pure MA process by applying lag operator polynomial division.

2. Truncate the resulting MA polynomial by enforcing the default tolerances.

For more details, see mldivide.

Tip

• If Mdl contains an AR or differencing polynomial (seasonal or nonseasonal) the MA representation of the model has infinite lag order. Consider specifying numObs in this case.

• If Mdl contains only MA polynomials, the IRF has length Mdl.Q + 1.

Example: 10

Data Types: double

Output Arguments

y — IRF

numeric column vector

IRF, returned as a numeric column vector. If you specify numObs, Y has length numObs. If you do not specify numObs, the tolerances of the underlying lag operator polynomial division algorithm determine the length of y.

y(j) is the impulse response of y_t at period j – 1. y(0) represents the impulse response during the period in which impulse applies the unit shock to the innovation (ε₀ = 1).

More About

Impulse Response Function

The impulse response function (IRF) of a univariate ARIMAX process is the dynamic response of the system to a single impulse (innovation shock).

Consider an ARIMAX model expressed as an MA process

$$y_t=m_t+\psi (L){\epsilon }_t,$$

where:

• ψ(L) is the infinite-degree MA lag operator polynomial $${\psi }_0+{\psi }_{1}L+{\psi }_2{L}^2+\dots$$ with scalar coefficients ψ_j, j = 0,1,2,… and ψ₀ = 1.

• m_t is the deterministic, innovation-free conditional mean of the process at time t.

The IRF measures the change to the response j periods in the future due to a change in the innovation at time t, for j = 0,1,2,…. Symbolically, the IRF at period j is

$$\frac{\partial y_{t+j}}{\partial {\epsilon }_t}={\psi }_j.$$

The sequence of dynamic multipliers [3], ψ₀, ψ₁, ψ₂,..., measures the sensitivity of the process to a purely transitory change in the innovation process, with past responses and future innovations set to 0. Because the partial derivative is taken with respect to the innovation, the presence of deterministic terms in the model, such as the constant and the exogenous regression component, has no effect on the impulse responses.

Properties of the IRF determine characteristics of the process:

• If the sequence $$\left\{{\psi }_j\right\}$$ is absolutely summable, y_t is a covariance-stationary stochastic process [5]. For a stationary stochastic process, the impact on the process due to a change in ε_t is not permanent, and the effect of the impulse decays to zero.

• Otherwise, the process y_t is nonstationary, and a change in ε_t affects the process permanently.

Because innovations can be interpreted as one-step-ahead forecast errors, the impulse response is also known as the forecast error impulse response.

Tips

• To improve performance of the filtering algorithm, specify the number of periods to include in the IRF numObs. When you do not specify numObs, impulse computes the IRF by using the lag operator polynomial division algorithm, which is relatively slow, to represent the input model Mdl as a truncated, infinite-degree, moving average model. The length of the resulting IRF is generally unknown.

References

[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.

[2] Enders, Walter. Applied Econometric Time Series. Hoboken, NJ: John Wiley & Sons, Inc., 1995.

[3] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.

[4] Lütkepohl, Helmut. New Introduction to Multiple Time Series Analysis. New York, NY: Springer-Verlag, 2007.

[5] Wold, H. A Study in the Analysis of Stationary Time Series. Uppsala, Sweden: Almqvist & Wiksell, 1938.