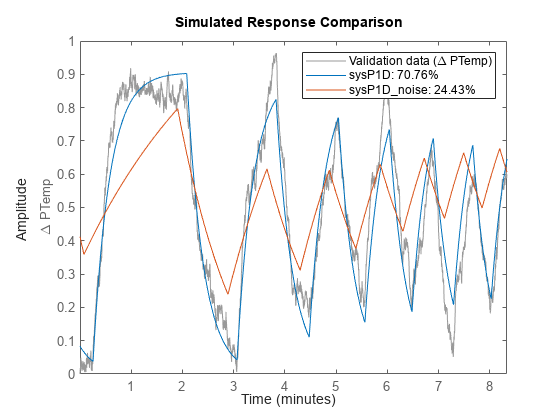
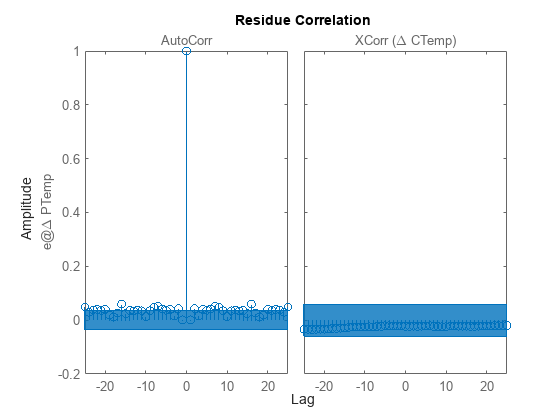
procest
Estimate process model using time-domain or frequency-domain data
Syntax
Description
Estimate Process Model
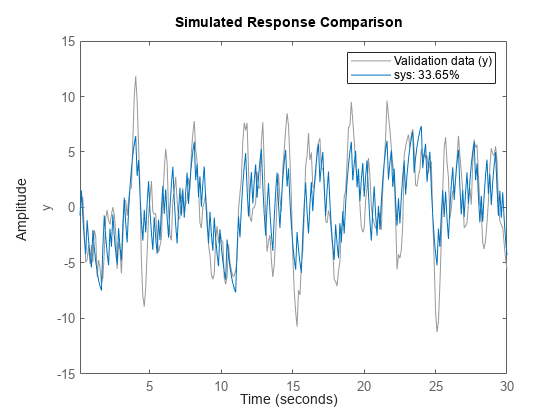
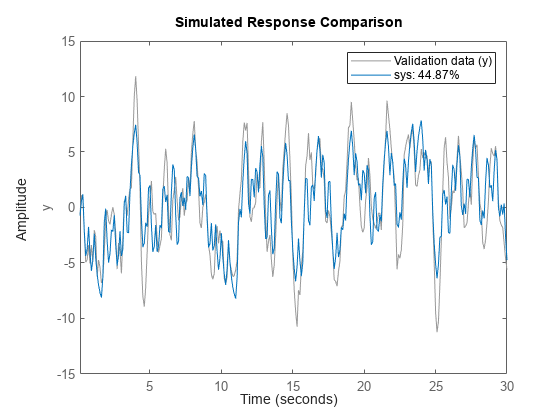
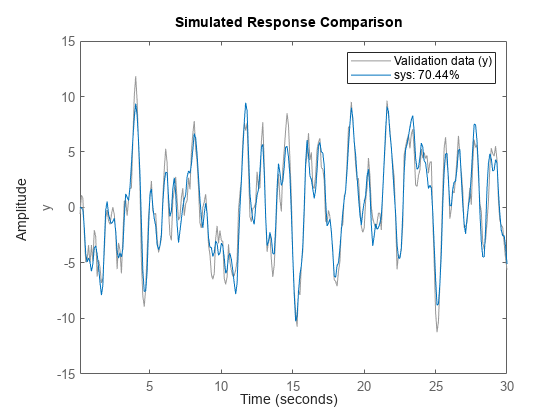
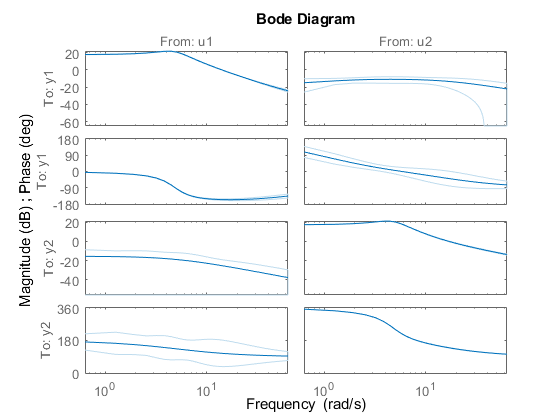
sys = procest(tt,type)sys using all the input and output
signals in the timetable tt. type defines the
structure of sys. You can use this syntax for SISO and MISO systems.
The function assumes that the last variable in the timetable is the single output
signal.
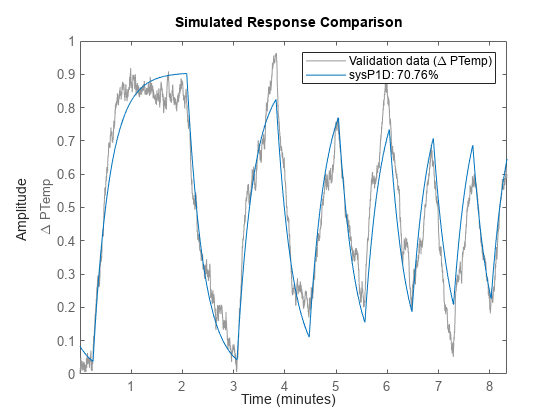
A simple SISO process model has a gain, a time constant, and a delay:
Kp is a proportional gain.
Tp1 is the time
constant of the real pole, and Td is the
transport delay (dead time). More complex process models can include zeroes, additional
time constants, complex poles, and integration. For more information on process models,
see idproc.
You cannot use procest to estimate time-series models, which are
models that contain no inputs. Use ar, arx, or armax for time-series models instead.
You cannot reliably estimate accurate process models from matrix-based data as you can with other model types. Process models are always continuous, and, because numeric matrices contain no sample time information, estimating continuous models from matrix-based data is generally not recommended. For information on converting matrices to timetables, see Convert SISO Matrix Data to Timetable.
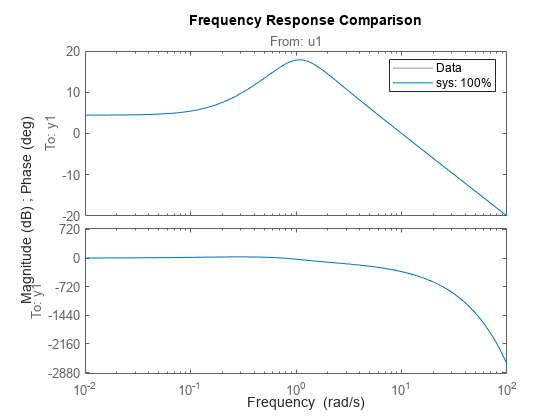
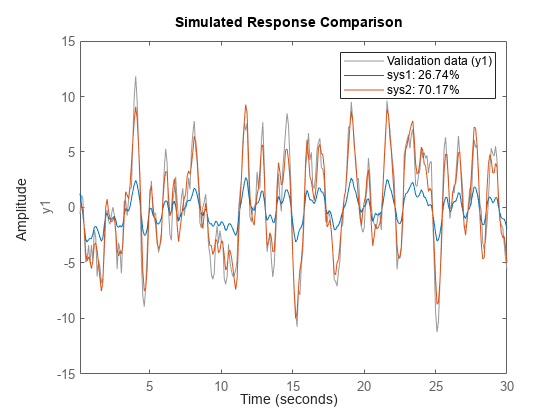
sys = procest(data,type)data. Use this
syntax especially when you want to estimate a process model using frequency-domain or
frequency response data, or when you want to take advantage of the additional information,
such as intersample behavior, data sample time, or experiment labeling, that data objects
provide.
sys = procest(___,Name,Value)sys = procest(tt,P1D,'InputDelay',2) specifies an input delay
of 2. You can use this syntax with any of the previous input-argument combinations
Configure Initial Parameters
Specify Additional Options
Return Estimated Offset and Initial Conditions
[
returns the estimated value of the offset in input signal. sys,offset] = procest(___)procest
automatically estimates the input offset when the model contains an integrator or when you
set the InputOffset estimation option to 'estimate'
using procestOptions.
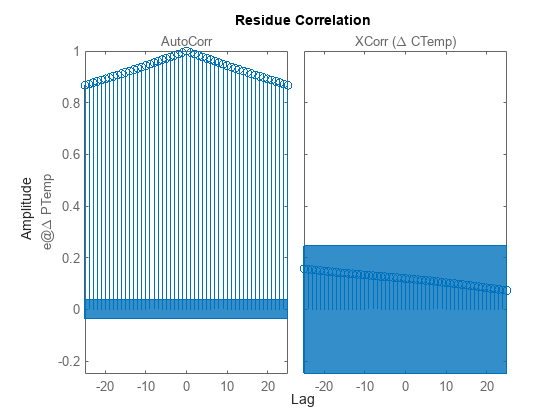
[
returns the estimated initial conditions as an sys,offset,ic] = procest(___)initialCondition
object. Use this syntax if you plan to simulate or predict the model response using the
same estimation input data and then compare the response with the same estimation output
data. Incorporating the initial conditions yields a better match during the first part of
the simulation.