fspecial3
Create predefined 3-D filter
Syntax
Description
h = fspecial3("average",hsize)h of size
hsize. Not recommended. Use imboxfilt3 instead.
h = fspecial3("gaussian",hsize,sigma)hsize with standard
deviation sigma. Not recommended. Use imgaussfilt3 instead.
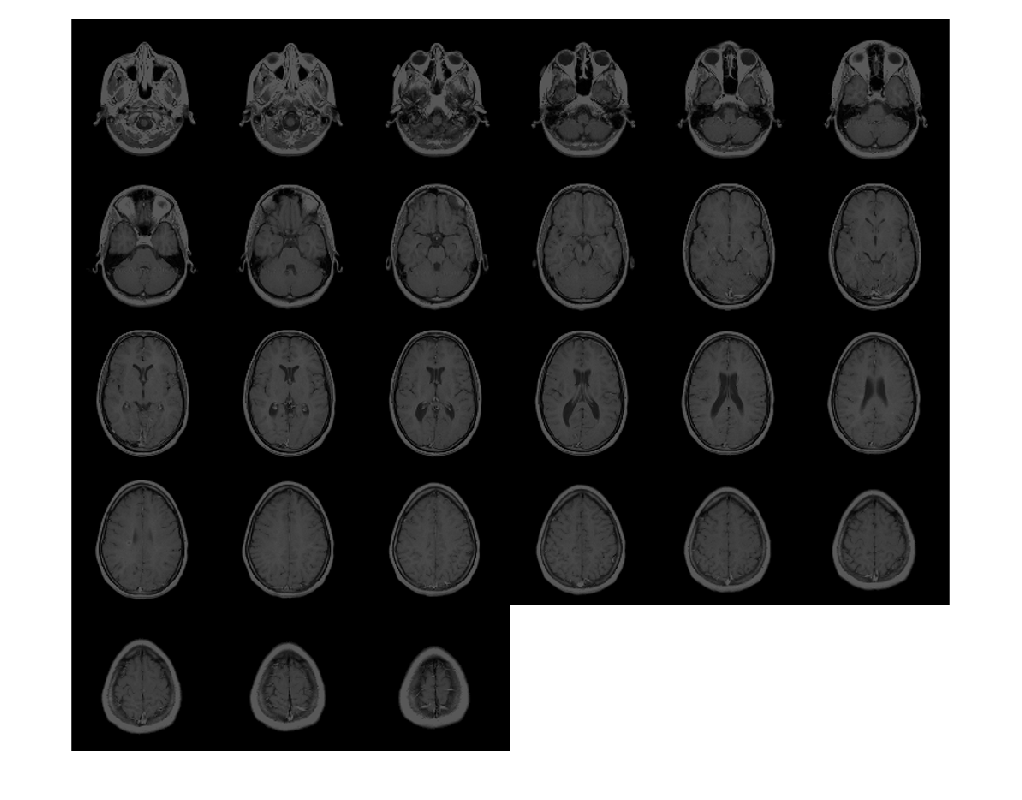
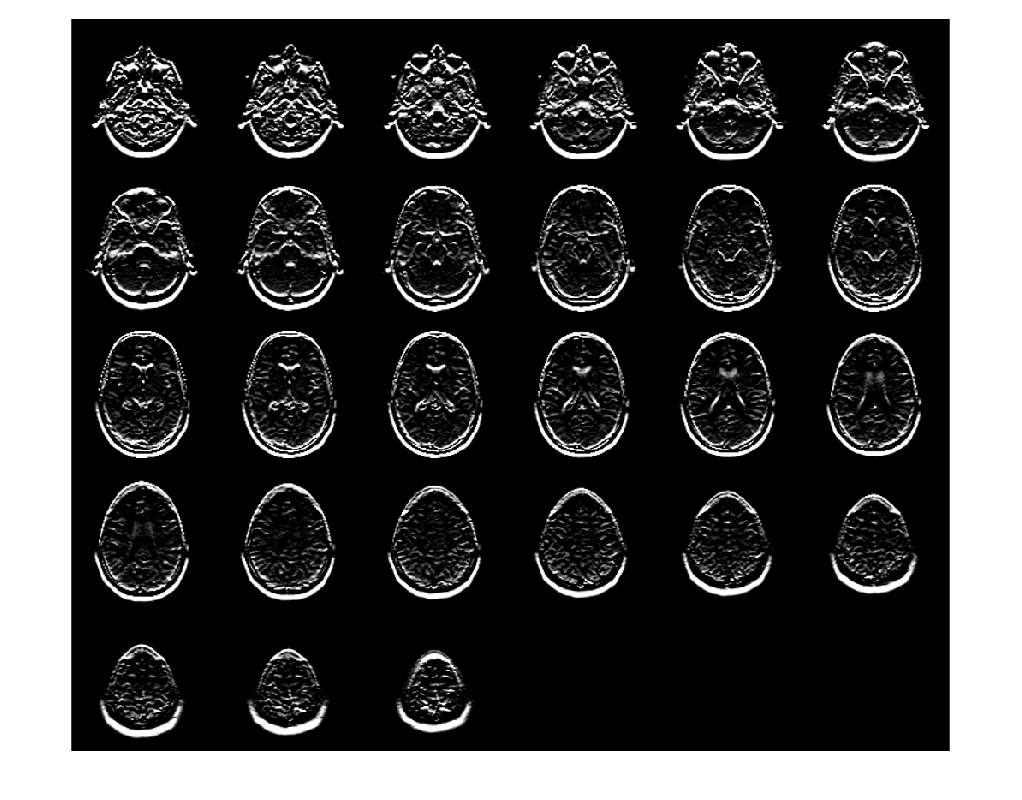
Examples
Input Arguments
Output Arguments
References
[1] Lindeberg, T., Scale-Space Theory in Computer Vision. Boston, MA: Kluwer Academic Publishers, 1994.
[2] Geometry-Driven Diffusion in Computer Vision. Edited by B. M. ter Haar Romeny. Boston, MA: Kluwer Academic Publishers, 1994.
[3] Engel, K., M. Hadwiger, J. M. Kniss, C. Rezk-Salama, and D. Weiskopf. Real-Time Volume Graphics. Wellesley, MA: A K Peters, Ltd., 2006, pp. 112–114.
Extended Capabilities
Version History
Introduced in R2018b
See Also
imfilter | fspecial | imboxfilt3 | imgaussfilt3 | edge3