Mean Square Error of Prediction for Estimated Ultimate Claims
This example shows a workflow for estimating ultimate claims using a developmentTriangle object with simulated reported claims and then calculating the corresponding mean square error of prediction (MSEP).
Actuaries use different techniques to estimate the ultimate claims for different years. In addition to the claim values, an actuary needs to know how well the estimates predict the outcomes of random variables and the uncertainties in the estimates for the ultimate claims. To measure the quality of the estimated ultimate claims, you can calculate the MSEP.
Load Data
load('InsuranceClaimsData.mat');
disp(head(data)); OriginYear DevelopmentYear ReportedClaims PaidClaims
__________ _______________ ______________ __________
2010 12 3995.7 1893.9
2010 24 4635 3371.2
2010 36 4866.8 4079.1
2010 48 4964.1 4487
2010 60 5013.7 4711.4
2010 72 5038.8 4805.6
2010 84 5059 4853.7
2010 96 5074.1 4877.9
Create developmentTriangle
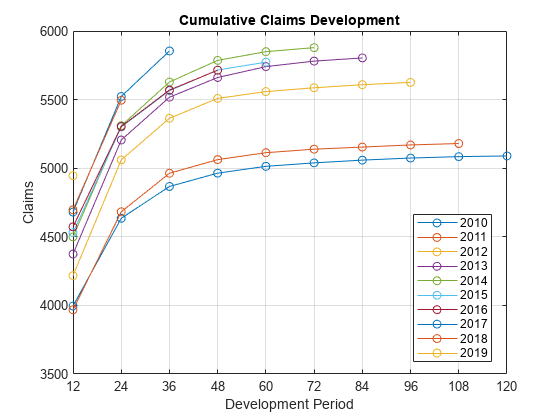
Create a developmentTriangle object and use claimsPlot to visualize the developmentTriangle. For more information on unpaid claims estimation, see Overview of Claims Estimation Methods for Non-Life Insurance
dTriangle = developmentTriangle(data,'Origin','OriginYear','Development','DevelopmentYear','Claims','ReportedClaims'); dTriangleTable = view(dTriangle); % Visualize the development triangle claimsPlot(dTriangle);
Analyze developmentTriangle
Use linkRatios to calculate the age-to-age factors.
factorsTable = linkRatios(dTriangle);
Use linkRatioAverages to calculate the averages of the age-to-age factors.
averageFactorsTable = linkRatioAverages(dTriangle);
dTriangle.SelectedLinkRatio = averageFactorsTable{'Volume-weighted Average',:};
dTriangle.TailFactor = 1;
selectedFactorsTable = cdfSummary(dTriangle);Display the full development triangle using the fullTriangle function.
fullTriangleTable = fullTriangle(dTriangle); disp(fullTriangleTable);
12 24 36 48 60 72 84 96 108 120 Ultimate
______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ________
2010 3995.7 4635 4866.8 4964.1 5013.7 5038.8 5059 5074.1 5084.3 5089.4 5089.4
2011 3968 4682.3 4963.2 5062.5 5113.1 5138.7 5154.1 5169.6 5179.9 5185.1 5185.1
2012 4217 5060.4 5364 5508.9 5558.4 5586.2 5608.6 5625.4 5636.7 5642.3 5642.3
2013 4374.2 5205.3 5517.7 5661.1 5740.4 5780.6 5803.7 5821.1 5832.7 5838.6 5838.6
2014 4499.7 5309.6 5628.2 5785.8 5849.4 5878.7 5900.8 5918.5 5930.3 5936.3 5936.3
2015 4530.2 5300.4 5565.4 5715.7 5772.8 5804.1 5825.9 5843.4 5855.1 5861 5861
2016 4572.6 5304.2 5569.5 5714.3 5775.4 5806.7 5828.6 5846.1 5857.7 5863.6 5863.6
2017 4680.6 5523.1 5854.4 6000.9 6065.1 6098 6120.9 6139.3 6151.6 6157.7 6157.7
2018 4696.7 5495.1 5804.4 5949.6 6013.3 6045.9 6068.6 6086.8 6099 6105.1 6105.1
2019 4945.9 5819.2 6146.7 6300.5 6367.9 6402.4 6426.5 6445.8 6458.7 6465.2 6465.2
Compute the total reserves using ultimateClaims.
IBNR = ultimateClaims(dTriangle) - dTriangle.LatestDiagonal; IBNR = array2table(IBNR, 'RowNames', dTriangleTable.Properties.RowNames, 'VariableNames', {'IBNR'}); IBNR{'Total',1} = sum(IBNR{:,:}); disp(IBNR);
IBNR
______
2010 0
2011 5.1857
2012 16.89
2013 34.886
2014 57.583
2015 88.148
2016 149.34
2017 303.29
2018 609.99
2019 1519.3
Total 2784.6
Calculate Estimated Standard Deviations
The developmentTriange link ratios are estimated using the formula:
Along, with the link ratios, the variance parameters are estimated as:
Since the last variance parameter cannot be estimated with the estimator , the Mack extrapolation method is used to estimate of :
Using this formula, you can compute the estimated conditional process standard deviations.
currentSelectedFactors = dTriangle.SelectedLinkRatio; estimatedStandardDeviations = currentSelectedFactors; for i=1:width(estimatedStandardDeviations)-1 estimatedStandardDeviations(1,i) = sqrt(sum(((factorsTable{1:end-i,i} - currentSelectedFactors(:,i)).^2).*dTriangleTable{1:end-i,i}) / (height(dTriangleTable)-i-1)); end estimatedStandardDeviations(1,end) = sqrt(min([estimatedStandardDeviations(1,end-1)^4 / estimatedStandardDeviations(1,end-2)^2, estimatedStandardDeviations(1,end-2)^2, estimatedStandardDeviations(1,end-1)^2]));
Calculate Reserves and Estimated Conditional Process Standard Deviations
Using the latest developmentTriange diagonal information and projected ultimate claims from the developmentTriangle object, the ReservesTable is calculated.
h = height(dTriangleTable);
ReservesTable = array2table(NaN(h, 9));
ReservesTable.Properties.RowNames = dTriangleTable.Properties.RowNames;
ReservesTable.Properties.VariableNames = {'Latest Diagonal','Projected Ultimate Claims','Reserves','Estimated conditional process standard deviation','Estimated conditional variational coefficient','Conditional Var_hat','variation for Var_hat','MSEP','MSEP Uncertainty'};
ReservesTable.("Latest Diagonal") = dTriangle.LatestDiagonal;
ReservesTable.("Projected Ultimate Claims") = ultimateClaims(dTriangle);
ReservesTable.("Reserves") = IBNR.IBNR(1:end-1,:);Estimate the conditional process variance for the ultimate claim of a single accident year as:
and estimate the conditional process variance for aggregated accident years as:
Calculate the estimated conditional variational coefficient for origin year relative to the estimated reserves as:
summationFactors = zeros(1,h); for i=length(summationFactors)-1:-1:1 summationFactors(i) = (estimatedStandardDeviations(1,i)^2 / currentSelectedFactors(1,i)^2) / dTriangle.LatestDiagonal(h-i+1) + summationFactors(i+1); end summationFactors = fliplr(summationFactors)'; ReservesTable.("Estimated conditional process standard deviation") = sqrt(ReservesTable.("Projected Ultimate Claims").^2 .* summationFactors); ReservesTable.("Estimated conditional variational coefficient") = ReservesTable.("Estimated conditional process standard deviation") ./ ReservesTable.("Reserves") * 100; ReservesTable('Total',:) = array2table([NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN, NaN]); ReservesTable{"Total","Reserves"} = sum(ReservesTable.("Reserves")(1:end-1)); ReservesTable{"Total","Estimated conditional process standard deviation"} = sqrt(sum(ReservesTable.("Estimated conditional process standard deviation")(1:end-1).^2)); ReservesTable{"Total","Estimated conditional variational coefficient"} = ReservesTable{"Total","Estimated conditional process standard deviation"} / ReservesTable{"Total","Reserves"} * 100; disp(ReservesTable(:,(2:5)));
Projected Ultimate Claims Reserves Estimated conditional process standard deviation Estimated conditional variational coefficient
_________________________ ________ ________________________________________________ _____________________________________________
2010 5089.4 0 0 NaN
2011 5185.1 5.1857 0.0072309 0.13944
2012 5642.3 16.89 0.011214 0.066397
2013 5838.6 34.886 0.014452 0.041426
2014 5936.3 57.583 2.7832 4.8333
2015 5861 88.148 5.8489 6.6353
2016 5863.6 149.34 11.634 7.7906
2017 6157.7 303.29 22.586 7.4472
2018 6105.1 609.99 36.512 5.9856
2019 6465.2 1519.3 77.982 5.1329
Total NaN 2784.6 90.01 3.2324
In addition to these calculated estimates, you can obtain the estimator for the conditional estimation error for origin year as:
where
factor1 = zeros(h,1);
factor2 = zeros(h,1);
factor1(2) = currentSelectedFactors(1,h-1)^2 + estimatedStandardDeviations(1,h-1)^2/sum(dTriangleTable{1,h-1});
factor2(2) = currentSelectedFactors(1,h-1)^2;
for i = 3:length(factor1)
factor1(i) = (currentSelectedFactors(1,h-i+1)^2 + estimatedStandardDeviations(1,h-i+1)^2/sum(dTriangleTable{1:i-1,h-i+1})) * factor1(i-1);
factor2(i) = currentSelectedFactors(1,h-i+1)^2 * factor2(i-1);
end
Var_hat = sqrt(dTriangle.LatestDiagonal.^2 .* (factor1 - factor2));
ReservesTable.("Conditional Var_hat")(1:end-1) = Var_hat;
ReservesTable.("variation for Var_hat")(1:end-1) = ReservesTable.("Conditional Var_hat")(1:end-1) ./ ReservesTable.("Reserves")(1:end-1) * 100;Using the previous formulas, the estimator for the conditional MSEP of the ultimate claim for a single origin year is:
And the estimator for the conditional MSEP of the ultimate claim for aggregated origin years is:
summationFactorsMSEP = zeros(h,1); for i=2:length(summationFactorsMSEP) summationFactorsMSEP(i) = (((estimatedStandardDeviations(1,h-i+1)^2 / currentSelectedFactors(1,h-i+1)^2)) * (inv(dTriangle.LatestDiagonal(i)) + inv(sum(dTriangleTable{1:i-1,h-i+1})))) + summationFactorsMSEP(i-1); end msep = sqrt(ReservesTable.("Projected Ultimate Claims")(1:end-1).^2 .* summationFactorsMSEP); ReservesTable.MSEP(1:end-1) = msep; ReservesTable.("MSEP Uncertainty")(1:end-1) = ReservesTable.MSEP(1:end-1) ./ ReservesTable.("Reserves")(1:end-1) * 100; ReservesTable{'Total','Conditional Var_hat'} = sqrt(sum(ReservesTable.("Conditional Var_hat")(1:end-1).^2)); ReservesTable{'Total','variation for Var_hat'} = ReservesTable{'Total','Conditional Var_hat'} / ReservesTable{'Total','Reserves'} * 100; disp(ReservesTable(:,[2,3,6,7]));
Projected Ultimate Claims Reserves Conditional Var_hat variation for Var_hat
_________________________ ________ ___________________ _____________________
2010 5089.4 0 0 NaN
2011 5185.1 5.1857 0.0072985 0.14074
2012 5642.3 16.89 0.0099066 0.058655
2013 5838.6 34.886 0.011503 0.032972
2014 5936.3 57.583 1.4539 2.5248
2015 5861 88.148 2.7754 3.1486
2016 5863.6 149.34 5.0379 3.3735
2017 6157.7 303.29 9.1852 3.0285
2018 6105.1 609.99 13.941 2.2854
2019 6465.2 1519.3 28.137 1.852
Total NaN 2784.6 33.25 1.1941
Calculate MSEP
Measure the quality of the estimated ultimate claims by calculating the MSEP and MSEP Uncertainty.
summationFactorsCovarianceTerm = zeros(h,1); for i=2:length(summationFactorsCovarianceTerm) summationFactorsCovarianceTerm(i) = ((estimatedStandardDeviations(1,h-i+1)^2 / currentSelectedFactors(1,h-i+1)^2) / sum(dTriangleTable{1:i-1,h-i+1})) + summationFactorsCovarianceTerm(i-1); end totalSum = 0; for i = 2:h totalSum = totalSum + sum(dTriangle.LatestDiagonal(i,1) * fullTriangleTable{i+1:end, h-i+1} * summationFactorsCovarianceTerm(i)); end covarianceTerm = 2 * totalSum; totalMSEP = sqrt(sum(ReservesTable.MSEP(1:end-1) .^ 2) + covarianceTerm); ReservesTable{'Total','MSEP'} = totalMSEP; ReservesTable{'Total','MSEP Uncertainty'} = ReservesTable{'Total','MSEP'} / ReservesTable{'Total','Reserves'} * 100; disp(ReservesTable(:,[1,2,3,8,9]));
Latest Diagonal Projected Ultimate Claims Reserves MSEP MSEP Uncertainty
_______________ _________________________ ________ ________ ________________
2010 5089.4 5089.4 0 0 NaN
2011 5179.9 5185.1 5.1857 0.010274 0.19812
2012 5625.4 5642.3 16.89 0.014963 0.088593
2013 5803.7 5838.6 34.886 0.018471 0.052945
2014 5878.7 5936.3 57.583 3.14 5.453
2015 5772.8 5861 88.148 6.474 7.3445
2016 5714.3 5863.6 149.34 12.678 8.4897
2017 5854.4 6157.7 303.29 24.383 8.0394
2018 5495.1 6105.1 609.99 39.083 6.4071
2019 4945.9 6465.2 1519.3 82.903 5.4568
Total NaN NaN 2784.6 100.45 3.6074
References
Wüthrich, Mario, and Michael Merz. Stochastic Claims Reserving Methods in Insurance. Hoboken, NJ: Wiley, 2008.
Friedland, Jacqueline. "Estimating Unpaid Claims Using Basic Techniques." Arlington, VA: Casualty Actuarial Society, 2010.
See Also
developmentTriangle | view | linkRatios | linkRatiosPlot | linkRatioAverages | cdfSummary | ultimateClaims | claimsPlot | fullTriangle | chainLadder | expectedClaims | bornhuetterFerguson | capeCod