plot
Plot first- and total-order Sobol indices and variances
Description
Examples
Load the tumor growth model.
sbioloadproject tumor_growth_vpop_sa.sbprojGet a variant with the estimated parameters and the dose to apply to the model.
v = getvariant(m1);
d = getdose(m1,'interval_dose');Get the active configset and set the tumor weight as the response.
cs = getconfigset(m1);
cs.RuntimeOptions.StatesToLog = 'tumor_weight';Simulate the model and plot the tumor growth profile.
sbioplot(sbiosimulate(m1,cs,v,d));
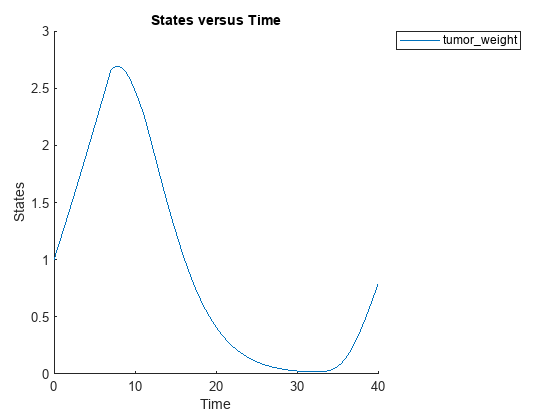
Perform global sensitivity analysis (GSA) on the model to find the model parameters that the tumor growth is sensitive to.
First, retrieve model parameters of interest that are involved in the pharmacodynamics of the tumor growth. Define the model response as the tumor weight.
modelParamNames = {'L0','L1','w0','k1','k2'};
outputName = 'tumor_weight';Then perform GSA by computing the first- and total-order Sobol indices using sbiosobol. Set 'ShowWaitBar' to true to show the simulation progress. By default, the function uses 1000 parameter samples to compute the Sobol indices [1].
rng('default');
sobolResults = sbiosobol(m1,modelParamNames,outputName,Variants=v,Doses=d,ShowWaitBar=true)sobolResults =
Sobol with properties:
Time: [444×1 double]
SobolIndices: [5×1 struct]
Variance: [444×1 table]
ParameterSamples: [1000×5 table]
Observables: {'[Tumor Growth].tumor_weight'}
SimulationInfo: [1×1 struct]
You can change the number of samples by specifying the 'NumberSamples' name-value pair argument. The function requires a total of (number of input parameters + 2) * NumberSamples model simulations.
Show the mean model response, the simulation results, and a shaded region covering 90% of the simulation results.
plotData(sobolResults,ShowMedian=true,ShowMean=false);
![Figure contains an axes object. The axes object with xlabel time, ylabel [Tumor Growth].tumor indexOf w baseline eight contains 12 objects of type line, patch. These objects represent model simulation, 90.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_02.png)
You can adjust the quantile region to a different percentage by specifying 'Alphas' for the lower and upper quantiles of all model responses. For instance, an alpha value of 0.1 plots a shaded region between the 100 * alpha and 100 * (1 - alpha) quantiles of all simulated model responses.
plotData(sobolResults,Alphas=0.1,ShowMedian=true,ShowMean=false);
![Figure contains an axes object. The axes object with xlabel time, ylabel [Tumor Growth].tumor indexOf w baseline eight contains 12 objects of type line, patch. These objects represent model simulation, 80.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_03.png)
Plot the time course of the first- and total-order Sobol indices.
h = plot(sobolResults);
% Resize the figure.
h.Position(:) = [100 100 1280 800];![Figure contains 12 axes objects. Axes object 1 with xlabel time, ylabel total variance contains an object of type line. Axes object 2 with xlabel time, ylabel fraction of unexplained variance contains 3 objects of type line. Axes object 3 with ylabel total order k2 contains 3 objects of type line. Axes object 4 with ylabel first order k2 contains 3 objects of type line. Axes object 5 with ylabel total order k1 contains 3 objects of type line. Axes object 6 with ylabel first order k1 contains 3 objects of type line. Axes object 7 with ylabel total order w0 contains 3 objects of type line. Axes object 8 with ylabel first order w0 contains 3 objects of type line. Axes object 9 with ylabel total order L1 contains 3 objects of type line. Axes object 10 with ylabel first order L1 contains 3 objects of type line. Axes object 11 with title sensitivity output [Tumor Growth].tumor_weight, ylabel total order L0 contains 3 objects of type line. Axes object 12 with title sensitivity output [Tumor Growth].tumor_weight, ylabel first order L0 contains 3 objects of type line.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_04.png)
The first-order Sobol index of an input parameter gives the fraction of the overall response variance that can be attributed to variations in the input parameter alone. The total-order index gives the fraction of the overall response variance that can be attributed to any joint parameter variations that include variations of the input parameter.
From the Sobol indices plots, parameters L1 and w0 seem to be the most sensitive parameters to the tumor weight before the dose was applied at t = 7. But after the dose is applied, k1 and k2 become more sensitive parameters and contribute most to the after-dosing stage of the tumor weight. The total variance plot also shows a larger variance for the after-dose stage at t > 35 than for the before-dose stage of the tumor growth, indicating that k1 and k2 might be more important parameters to investigate further. The fraction of unexplained variance shows some variance at around t = 33, but the total variance plot shows little variance at t = 33, meaning the unexplained variance could be insignificant. The fraction of unexplained variance is calculated as 1 - (sum of all the first-order Sobol indices), and the total variance is calculated using var(response), where response is the model response at every time point.
You can also display the magnitudes of the sensitivities in a bar plot. Darker colors mean that those values occur more often over the whole time course.
bar(sobolResults);
![Figure contains an axes object. The axes object with title sensitivity output [Tumor Growth].tumor_weight, xlabel Sobol Index, ylabel sensitivity input contains 22 objects of type patch, line. These objects represent first order, total order.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_05.png)
You can specify more samples to increase the accuracy of the Sobol indices, but the simulation can take longer to finish. Use addsamples to add more samples. For example, if you specify 1500 samples, the function performs 1500 * (2 + number of input parameters) simulations.
gsaMoreSamples = addsamples(gsaResults,1500)
The SimulationInfo property of the result object contains various information for computing the Sobol indices. For instance, the model simulation data (SimData) for each simulation using a set of parameter samples is stored in the SimData field of the property. This field is an array of SimData objects.
sobolResults.SimulationInfo.SimData
SimBiology SimData Array : 1000-by-7 Index: Name: ModelName: DataCount: 1 - Tumor Growth Model 1 2 - Tumor Growth Model 1 3 - Tumor Growth Model 1 ... 7000 - Tumor Growth Model 1
You can find out if any model simulation failed during the computation by checking the ValidSample field of SimulationInfo. In this example, the field shows no failed simulation runs.
all(sobolResults.SimulationInfo.ValidSample)
ans = 1×7 logical array
1 1 1 1 1 1 1
SimulationInfo.ValidSample is a table of logical values. It has the same size as SimulationInfo.SimData. If ValidSample indicates that any simulations failed, you can get more information about those simulation runs and the samples used for those runs by extracting information from the corresponding column of SimulationInfo.SimData. Suppose that the fourth column contains one or more failed simulation runs. Get the simulation data and sample values used for that simulation using getSimulationResults.
[samplesUsed,sd,validruns] = getSimulationResults(sobolResults,4);
You can add custom expressions as observables and compute Sobol indices for the added observables. For example, you can compute the Sobol indices for the maximum tumor weight by defining a custom expression as follows.
% Suppress an information warning that is issued during simulation. warnSettings = warning('off', 'SimBiology:sbservices:SB_DIMANALYSISNOTDONE_MATLABFCN_UCON'); % Add the observable expression. sobolObs = addobservable(sobolResults,'Maximum tumor_weight','max(tumor_weight)','Units','gram');
Plot the computed simulation results showing the 90% quantile region.
h2 = plotData(sobolObs,ShowMedian=true,ShowMean=false); h2.Position(:) = [100 100 1280 800];
![Figure contains 2 axes objects. Axes object 1 with ylabel Maximum tumor_weight contains 12 objects of type line, patch. One or more of the lines displays its values using only markers These objects represent model simulation, 90.0% region, median value. Axes object 2 with xlabel time, ylabel [Tumor Growth].tumor_weight contains 12 objects of type line, patch. These objects represent model simulation, 90.0% region, median value.](../../examples/simbio/win64/PerformGSAByComputingFirstAndTotalSobolIndicesExample_06.png)
You can also remove the observable by specifying its name.
gsaNoObs = removeobservable(sobolObs,'Maximum tumor_weight');Restore the warning settings.
warning(warnSettings);
Input Arguments
Results containing the first- and total-order Sobol indices, specified as a SimBiology.gsa.Sobol object.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: h = plot(results,'Observables','tumor_weight') specifies to
plot Sobol indices corresponding to the tumor weight response.
Input parameters to plot, specified as a character vector, string, string vector, cell
array of character vectors, or vector of positive integers indexing into the columns of
the resultsObject.ParameterSamples table. Use this name-value
argument to select parameters and plot their corresponding GSA results. By default, all
input parameters are included in the plot.
Data Types: double | char | string | cell
Model responses or observables to plot, specified as a character vector, string, string
vector, cell array of character vectors, or vector of positive integers indexing into
resultsObject.Observables. By default, the function plots GSA
results for all model responses or observables.
Data Types: double | char | string | cell
Color of the first- and total-order Sobol indices, specified as a three-element
row vector, hexadecimal color code, color name, or a short name. By default, the
function uses the first MATLAB® default color for the first order and the second default color for the
total order. To view the default color order, enter
get(groot,'defaultAxesColorOrder') or see the ColorOrder property.
For details on valid color names and corresponding RGB triplets and hexadecimal codes, see Specify Plot Colors.
Example: 'Color',[0.4,0.3,0.2]
Data Types: double
Color of the total and unexplained variances, specified as a three-element row
vector, hexadecimal color code, color name, or a short name. By default, the function
uses the color black [0,0,0].
For details on valid color names and corresponding RGB triplets and hexadecimal codes, see Specify Plot Colors.
Example: 'VarianceColor',[0.2,0.5,0.8]
Data Types: double
Color of the delimiting lines, specified as a three-element row vector,
hexadecimal color code, color name, or a short name. By default, the function uses
the color black [0,0,0].
For details on valid color names and corresponding RGB triplets and hexadecimal codes, see Specify Plot Colors.
Example: 'DelimiterColor',[0.2,0.5,0.8]
Data Types: double
Output Arguments
Handle to the figure, specified as a figure handle.
References
[1] Saltelli, Andrea, Paola Annoni, Ivano Azzini, Francesca Campolongo, Marco Ratto, and Stefano Tarantola. “Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index.” Computer Physics Communications 181, no. 2 (February 2010): 259–70. https://doi.org/10.1016/j.cpc.2009.09.018.
Version History
Introduced in R2020a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)