Spectrum Analyzer
Display frequency spectrum of time-domain signals
Libraries:
RF Blockset /
Circuit Envelope /
Utilities
Description
Note
The Spectrum Analyzer block in RF Blockset™ provides a subset of the functionality provided by the DSP System Toolbox™ block with the same name. This page describes the block configuration and functionality available with a RF Blockset license.
If you also have a DSP System Toolbox license, then the Spectrum Analyzer block in the RF Blockset > Utilities library is identical to the block in the DSP System Toolbox > Sinks library. For more information, see Spectrum Analyzer (DSP System Toolbox).
The Spectrum Analyzer block displays frequency spectra of input signals with discrete sample times.
In a RF Blockset model, to use a Spectrum Analyzer block instead of a regular scope:
Add a Spectrum Analyzer block to your block diagram.
If your model uses a variable-step solver, also add a Rate Transition block and connect it to the input port of the Spectrum Analyzer block. Set the Output port sample time parameter to the sample time you want the Spectrum Analyzer to use.
If your model uses a local solver, then it outputs physical signals with discrete sample times and you do not need to add a Rate Transition block. However, if you need to downsample from the solver fixed step size, you can use a Rate Transition block. For more information on using local solvers, see Making Optimal Solver Choices for Physical Simulation.
Use a PS-Simulink Converter block to connect the physical output signal of interest to the input port of the Spectrum Analyzer block (or to the input port of the Rate Transition block, if you are using one). For more information, see Connecting Simscape Diagrams to Simulink Sources and Scopes. You can also use additional signal processing blocks between the PS-Simulink Converter and the Spectrum Analyzer blocks to enhance signal quality.
Run the simulation. Once the simulation is complete, the Spectrum Analyzer, referred to here as the scope, opens and displays the frequency spectrum of the signal.
Programmatic Control
You can configure and display the Spectrum Analyzer settings from the command line with
the SpectrumAnalyzerBlockConfiguration object.
Examples
Analysis of Frequency Response of RF System
Analyze the frequency response of an RF system.
Ports
Input
Connect the signals you want to visualize. You can have up to 96 input ports. Input signals must have these characteristics:
Signal Domain — Frequency or time signals.
Type — Discrete signals.
Data type — Any data type that Simulink® supports. See Data Types Supported by Simulink.
Dimension — One dimensional (vector), two dimensional (matrix), or multidimensional (array) signals. Input signal must have a fixed number of channels. See Signal Dimensions and Determine Signal Dimensions.
The Spectrum Analyzer block supports variable-size input signals, that is, the frame size of the signals can change during simulation. When the signal frame size changes, the sample rate the scope uses changes accordingly, which in turn updates the frequency span of the spectrum display.
The Spectrum Analyzer block accepts fixed-point input, but
converts it to double for display.
This port is unnamed until you enable the RBW port. (since R2024a)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Complex Number Support: Yes
Specify the resolution bandwidth in Hz through this port. RBW defines the smallest positive frequency that can be resolved by the scope. You can also specify the RBW value using the RBW (Hz) parameter on the Estimation tab.
Dependency
To enable this port, set the RBW (Hz) parameter
on the Estimation tab to Input
port.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | Boolean | fixed point
Parameters
This section lists the block parameters for the Spectrum Analyzer block in Simscape™ and RF Blockset. For a complete list of parameters, see Spectrum Analyzer (DSP System Toolbox).
Scope Tab
Views
Set the type of spectrum to display as one of these values:
Power— Spectrum Analyzer shows the power spectrum.Power Density— Spectrum Analyzer shows the power spectral density. The power spectral density is the squared magnitude of the spectrum normalized to a bandwidth of 1 Hz.RMS— Spectrum Analyzer shows the root mean squared spectrum. Use this option to view the frequency of voltage or current signals.
Tunable: Yes
Programmatic Use
Block Parameter:
SpectrumType |
| Type: character vector or string scalar |
Data Types: char | string
Bandwidth
Specify the sample rate the scope uses in Hz as one of the following:
Inherited— Use this option to specify the same sample rate as the input signal.Positive scalar — The sample rate you specify must be at least twice the sample rate of the input signal. Otherwise, you might see unexpected behavior when visualizing your signal in the scope due to aliasing.
When the signal frame size changes, the sample rate the scope uses changes accordingly, which in turn updates the frequency span of the spectrum display.
To display the sample rate on the status bar, click the
icon in the status bar and select Sample Rate.
Programmatic Use
Block Parameter:
SampleRate, SampleRateSource |
Type:
double |
Tunable: Yes
Specify the offset to apply to the frequency axis (x-axis) in units of Hz as one of the following:
Scalar — Apply the same frequency offset to all channels.
Vector — Apply a specific frequency offset for each channel. The vector length must be equal to the number of input channels.
The overall span must fall within the Nyquist Frequency Interval. You can control the overall span in different ways based on how you set the Span (Hz) parameter.
Tunable: Yes
Programmatic Use
Block
Parameter:
FrequencyOffset |
Type:
double |
Configuration > Spectrum Analyzer Settings
The number of input ports to the block, specified as an integer between 1 and 96. To change the number of input ports, drag a new input signal line to the block and the block automatically creates new ports.
Programmatic Use
Block Parameter:
NumInputPorts |
| Type: character vector or string scalar |
| Values: scalar between 1 and 96 |
Select this parameter to automatically open the Spectrum Analyzer window when you run the simulation.
Programmatic Use
Block Parameter:
OpenAtSimulationStart |
| Type: logical |
Since R2024b
Specify the precision of numeric values in the scope display as a positive integer in the range [1, 15].
Tunable: Yes
Specify the y-axis label in the Spectrum display as a
character vector or a string scalar. To display signal units, add
(%<SignalUnits>) to the label. When simulation
starts, Simulink replaces (%SignalUnits) with the units
associated with the signals. For example, for a velocity signal with units
of m/s
enter:
Velocity (%<SignalUnits>)
Tunable: Yes
Programmatic Use
Block Parameter:
YLabel |
| Type: character vector or string scalar |
Specify the y-axis limits in the Spectrum Analyzer
display as a two-element numeric vector of the form [ymin
ymax]. The units of the y-axis limits
depend on the Spectrum Unit in the
Spectrum tab.
Tunable: Yes
Programmatic Use
Block Parameter:
YLimits |
Type:
double |
Specify the display title. Enter %<SignalLabel>
to use the signal labels in the Simulink model as the axes titles.
Tunable: Yes
Programmatic Use
Block
Parameter:
Title |
| Type: character vector or string |
Select this check box to show the grid in the Spectrum Analyzer display.
Tunable: Yes
Programmatic Use
Block
Parameter:
ShowGrid |
Type:
logical |
Specify whether to display a Line or
Stem plot in the Spectrum display.
You can individually control the type of plot for each line. Select the line and set the Plot Type accordingly. (since R2025a)
Tunable: Yes
Programmatic Use
Block Parameter:
PlotType |
| Type: character vector or string scalar |
Specify the font size of the ticks, labels, title, and measurements of the scope as a positive scalar.
Tunable: Yes
Programmatic Use
Block Parameter: - |
| Type: double |
Specify the background color in the scope figure.
Tunable: Yes
Specify the background color of the axes.
Tunable: Yes
Specify the color of the labels, grid, and the channel names in the legend.
Tunable: Yes
Specify the channel for which you want to modify the visibility, line color, style, width, and marker properties.
Tunable: Yes
Select this check box to display the channel you have selected. If you clear this check box, the selected channel is no longer visible. You can also click the signal name in the legend to control its visibility. For more details, see Legend.
Tunable: Yes
Specify the line style for the selected channel.
Tunable: Yes
Specify the line width for the selected channel.
Tunable: Yes
Specify a data point marker for the selected channel. This parameter is similar to the Marker property for plots. You can choose any of the marker symbols from the drop-down list.
Tunable: Yes
Specify the line color for the selected channel.
Tunable: Yes
Configuration
Click the Legend button to enable the Spectrum Analyzer to display. The legend displays the signal names from the model. For signals with multiple channels, the scope appends a channel index after the signal name. Continuous signals have straight lines before their names and discrete signals have step-shaped lines.
You can control which signals are visible using the legend. To hide a
signal in the scope legend, click the signal name. To display the signal,
click the signal name again. Alternatively, you can control which signal is
visible using the Visible parameter in the
Spectrum Analyzer Settings (![]() ).
).
To display only one signal and hide all other signals, right-click the name of the signal you want the scope to display. To show all signals, press Esc.
Note
The legend displays only the first 20 signals. You cannot view or control any additional signals from the legend.
Programmatic Use
Block Parameter:
ShowLegend |
Type:
logical |
Tunable: Yes
Share
Click this button to copy the scope display to the clipboard. You can preserve the color in the display by selecting Preserve Colors in the Copy to Clipboard drop down.
When you copy the display to the clipboard using the Copy to Clipboard and the Print options in the Scope tab > Share section, select this parameter for the scope to preserve the colors.
To access Preserve Colors, click the drop-down arrow for Copy to Clipboard.
Tunable: Yes
Click this button to save the scope display as an image or a PDF or to print the display.
Estimation Tab
Frequency Resolution
Specify the resolution bandwidth in Hz. This parameter defines the smallest positive frequency
that can be resolved by the scope. By default, this parameter is set to
Auto. In this case, the spectrum analyzer determines the
appropriate value to ensure that there are 1024 RBW intervals over the specified
frequency span.
If you set this parameter to Input port, you can specify
the RBW value through an input port on the block.
If you set this parameter to a numeric value, the value must allow at least two RBW intervals over the specified frequency span. In other words, the ratio of the overall frequency span to RBW must be greater than two:
To display this property on the status bar, click the
icon in the status bar and select RBW.
Programmatic Use
Block Parameter: RBWSource, RBW |
Type: character vector, string scalar, double |
Tunable: Yes
Averaging
Specify the smoothing method as one of the following:
Exponential— The block computes the average over samples weighted by an exponentially decaying forgetting factor. Use the Forgetting Factor parameter to specify the weighted forgetting factor.VBW— The block uses a lowpass filter to smooth the trace and decrease the noise. Use the VBW (Hz) parameter to specify the video bandwidth (VBW) value.Running— Running average of the last Q samples. Use the Spectral Averages parameter to specify Q. (since R2025a)
For more information on the averaging methods, see Averaging Method.
Tunable: Yes
Programmatic Use
Block Parameter:
AveragingMethod |
| Type: character vector or string scalar |
Specify the video bandwidth as one of the following:
Auto–– The Spectrum Analyzer adjusts the VBW such that the equivalent forgetting factor is 0.9.Input port–– An input port appears on the scope and you can specify the VBW value through this port.Positive scalar –– You specify a positive scalar. The Spectrum Analyzer adjusts the VBW using this value. The value you specify must be less than or equal to Sample Rate (Hz)/2.
For more details on the video bandwidth method, see Averaging Method.
The Spectrum Analyzer shows the VBW value in the status bar at the bottom
of the display. To display the VBW value, click the ![]() icon in the status bar and select
icon in the status bar and select
VBW.
Dependency
To enable this parameter, set Averaging Method to
VBW.
Programmatic Use
Block Parameter:
VBWSource, VBW |
Type:
double |
Tunable: Yes
Specify the forgetting factor of the exponential weighted averaging method as a scalar in the range [0,1].
Tunable: Yes
Dependency
To enable this parameter, set Averaging Method to
Exponential.
Programmatic Use
Block Parameter:
ForgettingFactor |
Type:
double |
Since R2025a
Specify the number of spectral averages Q as a positive integer.
The Spectrum Analyzer computes the current power spectrum estimate by computing a running average of the last Q power spectrum estimates.
Dependency
To enable this parameter, set Averaging Method to
Running.
Programmatic Use
Block Parameter:
SpectralAverages |
Type:
double |
Data Types: double
Window Options
Specify the windowing method to apply to the spectrum. Windowing is used to control the effect of sidelobes in spectral estimation. The window you specify affects the window length required to achieve a resolution bandwidth and the required number of samples per update. For more information about windowing, see Windows (Signal Processing Toolbox).
You can access additional windowing algorithms if you install DSP System Toolbox.
Tunable: Yes
Programmatic Use
Block Parameter:
Window |
| Type: character vector or string scalar |
Specify the percentage of overlap between the previous and the current buffered data segments as a scalar in the range [0 100). The overlap creates a window segment that the scope uses to compute a spectral estimate. The value must be greater than or equal to zero and less than 100.
Tunable: Yes
Programmatic Use
Block Parameter:
OverlapPercent |
Type:
double |
Measurements Tab
Channel
The channel for which you need to obtain measurements, specified as a positive integer in the range [1 N], where N is the number of input channels.
Tunable: Yes
Dependency
To enable this parameter, pass some data through the scope.
Programmatic Use
See MeasurementChannel.
Cursors
Click the Data Cursors button to enable data cursor measurements. Each cursor tracks a vertical line along the signal. The scope displays the difference between x- and y-values of the signal at the two cursors in the box between the cursors.
Tunable: Yes
Programmatic Use
See Enabled.
Select this parameter to position the cursors on the signal data points.
Tunable: Yes
Programmatic Use
See SnapToData.
Select this parameter to lock the frequency difference between the two cursors.
Tunable: Yes
Programmatic Use
See LockSpacing.
Peaks
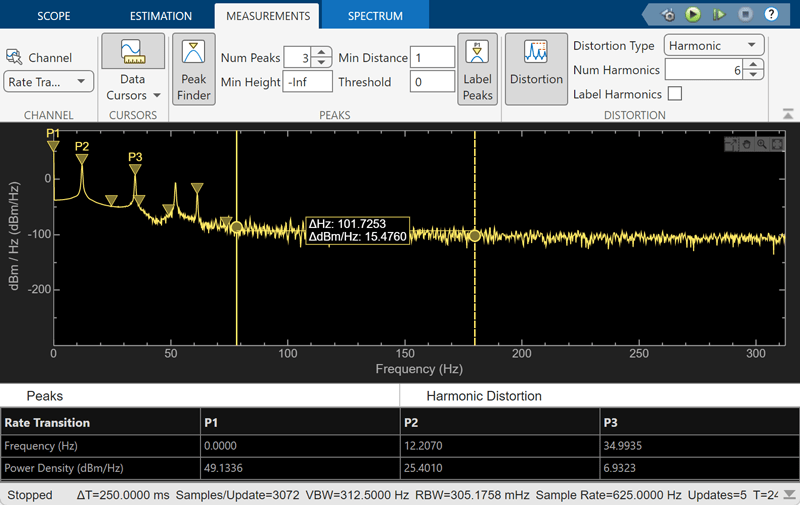
Click the Peak Finder button to enable peak finder measurements. An arrow appears on the plot at each maxima and a Peaks panel appears at the bottom of the scope window.
Tunable: Yes
Programmatic Use
See Enabled.
Specify the maximum number of peaks to show as a positive integer less than 100.
Tunable: Yes
Programmatic Use
See NumPeaks.
Specify the level above which the scope detects peaks as a real scalar.
Tunable: Yes
Programmatic Use
See MinHeight.
Specify the minimum number of samples between adjacent peaks as a positive integer.
Tunable: Yes
Programmatic Use
See MinDistance.
Specify the minimum difference between the height of the peak and its neighboring samples as a nonnegative scalar.
Tunable: Yes
Programmatic Use
See Threshold.
Click the Label Peaks button to label the peaks. The scope displays the labels (P1, P2, …) above the arrows in the plot.
Tunable: Yes
Programmatic Use
See LabelPeaks.
Distortion
Click the Distortion button to enable distortion measurements. A Distortion panel appears at the bottom of the scope window when you click this button.
Tunable: Yes
Programmatic Use
See Enabled.
Specify the type of measurement data to display as Harmonic or Intermodulation. For more details, see Distortion Measurements.
Tunable: Yes
Programmatic Use
See Type.
Specify the number of harmonics to measure as a positive integer less than or equal to 99.
Tunable: Yes
Dependency
To enable this parameter, set Distortion Type to Harmonic.
Programmatic Use
See NumHarmonics.
When you select this parameter, the spectrum analyzer adds numerical labels to harmonics in the spectrum display.
Tunable: Yes
Programmatic Use
See LabelValues.
When you select this parameter, the spectrum analyzer adds numerical labels to the first-order intermodulation product and third-order frequencies in the spectrum analyzer display.
Tunable: Yes
Programmatic Use
See LabelValues.
Spectrum Tab
Trace Options
Select this check box to enable a two-sided spectrum view. In this view, the spectrum analyzer shows both negative and positive frequencies. When the input signal is complex-valued, you must select this parameter. If you clear this check box, the spectrum analyzer shows a one-sided spectrum with positive frequencies only. In this case, the input signal data must be real valued.
When you clear this check box, the spectrum analyzer uses power folding.
The y-axis values are twice the amplitude that they
would be if you were to select this parameter, except at
0 and the Nyquist frequency. A one-sided
power spectral density (PSD) contains the total power of the signal in
the frequency interval from DC to half the Nyquist rate. For more
information, see pwelch (Signal Processing Toolbox).
Tunable: Yes
Programmatic Use
Block
Parameter:
PlotAsTwoSidedSpectrum |
Type:
logical |
Scale
Specify the scale to display frequencies as
Linear or Log.
When the frequency span contains negative frequency values, you cannot
choose the logarithmic option.
Tunable: Yes
Dependency
To set the Frequency Scale to
Log, clear the Two-Sided
Spectrum check box in the Trace
Options section in the Spectrum
tab. If you select the Two-Sided Spectrum check
box, then the Frequency Scale parameter is set to
Linear.
Programmatic Use
Block Parameter:
FrequencyScale |
| Type: character vector or string scalar |
Specify the reference load in ohms that the Spectrum Analyzer uses as a reference to compute the power values.
Tunable: Yes
Dependency
To enable this parameter, set:
Spectrum type to
PowerorPower Density.
Programmatic Use
Block
Parameter:
ReferenceLoad |
Type:
double |
Specify the units in which the Spectrum Analyzer displays the power values as one of the following:
dBmdBVdBuV(since R2023b)VrmsdBm/Hz
Tunable: Yes
Dependency
The units available depend on the value you choose for the Spectrum parameter in the Scope tab.
| Scope tab > Spectrum option | Available Units |
|---|---|
Power | dBm |
Power Density | dBm/Hz |
RMS | dBV, dBuV (since R2023b),
Vrms |
Programmatic Use
Block Parameter:
SpectrumUnits |
| Type: character vector or string scalar |
Property Inspector Only
Input channel names, specified as a character vector, string, or array. The names appear in
the legend, Settings, and Measurements
panels. If you do not specify the names, the scope labels the channels as
Channel 1, Channel 2, etc.
Example: ["A","B"]
Dependency
To see channel names, select Legend in the Scope tab.
Programmatic Use
Block Parameter: ChannelNames |
| Type: cell array of character vectors or string array |
Auto— If you have not specified Title and Y-Label, the scope maximizes all plots.On— The scope maximizes all plots and hides all values in Title and Y-label.Off— The scope does not maximize plots.
Hover over the Spectrum Analyzer to see the maximize axes button
![]() .
.
Tunable: Yes
Programmatic Use
Block Parameter:
MaximizeAxes |
| Type: character vector or string scalar |
OnceAtStop— Scale y-axis after simulation completes.Manual— Manually scale y-axis range with the Scale Y-axis Limits toolbar button.Auto— Scale y-axis range during and after simulation.Updates— Scale y-axis after the number of time steps specified in the Number of Updates text box (100by default). Scaling occurs only once during each run.
Tunable: Yes
Programmatic Use
Block Parameter: AxesScaling |
| Type: character vector or string scalar |
Set this property to delay auto scaling the y-axis.
Tunable: Yes
Dependency
To enable this property, set Axes Scaling to Updates.
Programmatic Use
Block Parameter: AxesScalingNumUpdates |
| Type: character vector or string scalar |
| Values: scalar |
More About
Measure signal values using vertical waveform cursors that track along the signal.
When you click the Data Cursors button in the Measurements tab of the Spectrum Analyzer, the spectrum display shows vertical cursors on each signal. Each cursor tracks a vertical line along the signal. The scope displays the difference between x- and y-values of the signal at the two cursors in the box between the cursors.
To enable cursor measurements, click the Data Cursors button in the Measurements tab. The cursors appear only when the Spectrum Analyzer has at least one signal in its display.
You can use the mouse to move the vertical cursors left and right.
In the Measurements tab, click the Data Cursors drop-down arrow to select one of these options:
Snap to Data — To position the cursors on the signal data points.
Lock Cursor Spacing — To lock the frequency difference between the two cursors.
For modifying the cursor measurements programmatically, see the CursorMeasurementsConfiguration
object.
Compute and display peak values in the scope display.
When you click the Peak Finder button in the Measurements tab of the Spectrum Analyzer, an arrow appears on the plot at each maxima and a Peaks panel appears at the bottom of the scope window. The Spectrum Analyzer computes peaks from the portion of the input signal that is currently on display in the scope, and the Peaks panel shows the peak values and the frequencies at which they occur.
The Peaks section in the Measurements tab allows you to specify the number of peaks you want the scope to display, the minimum height above which you want the scope to detect peaks, the minimum distance between peaks, and label the peaks.
The Spectrum Analyzer algorithm defines a peak as a local maximum with lower values present on either side of the peak. It does not consider end points as peaks. For more information on the algorithm, see the findpeaks (Signal Processing Toolbox) function.
The peaks are valid for any units of the input signal. The letter after the value associated with each measurement indicates the abbreviation for the appropriate International System of Units (SI) prefix, such as m for milli-. For example, if the input signal is measured in volts, an m next to a measurement value indicates that this value is in units of millivolts.
For modifying the peak finder measurements programmatically, see the PeakFinderConfiguration object. For more information on these settings in the
UI, see Peaks.
Measure harmonic distortion and intermodulation distortion.
When you click the Distortion button in the Distortion section of the Measurements tab, a distortion panel opens at the bottom of the Spectrum Analyzer window. This panel shows the harmonic and distortion measurement values for the input signal currently on display in the scope. The Distortion section in the Measurements tab allows you to specify the distortion type, number of harmonics, and even label the harmonics.
Note
For an accurate measurement, ensure that the fundamental signal (for harmonics) or
primary tones (for intermodulation) is larger than any spurious or harmonic content. To
do so, you may need to adjust the resolution bandwidth (RBW) of the
Spectrum Analyzer. Make sure that the bandwidth is low enough to isolate the signal and
harmonics from spurious noise content. In general, you should set the RBW value such
that there is at least a 10 dB separation between the peaks of the sinusoids and the
noise floor. You also might need to select a different spectral window to obtain a valid
measurement.
You can set the Distortion Type parameter to one of these values:
Harmonic–– SelectHarmonicif your input is a single sinusoid.Intermodulation–– SelectIntermodulationif your input is two equal-amplitude sinusoids. Intermodulation can help you determine distortion when the scope uses only a small portion of the available bandwidth.
See Distortion Measurements for information on how distortion measurements are calculated.
When you set the Distortion Type to Harmonic,
these fields appear in the Harmonic Distortion panel at the bottom
of the Spectrum Analyzer window.
H1 — Fundamental frequency in Hz and its power in decibels of the measured power referenced to 1 milliwatt (dBm).
H2, H3, ... — Harmonics frequencies in Hz and their power in decibels relative to the carrier (dBc). If the harmonics are at the same level or exceed the fundamental frequency, reduce the input power.
THD — Total harmonic distortion. This value represents the ratio of the power in the harmonics D to the power in the fundamental frequency S. If the noise power is too high in relation to the harmonics, the THD value is not accurate. In this case, lower the resolution bandwidth or select a different spectral window.
SNR — Signal-to-noise ratio (SNR). This value represents the ratio of the power in the fundamental frequency S to the power of all nonharmonic content N, including spurious signals, in decibels relative to the carrier (dBc).
If you see
––as the reported SNR, the total nonharmonic content of your signal is less than 30% of the total signal.SINAD — Signal-to-noise-and-distortion ratio. This value represents the ratio of the power in the fundamental frequency S to all other content (including noise N and harmonic distortion D) in decibels relative to the carrier (dBc).
SFDR — Spurious-free dynamic range (SFDR). This value represents the ratio of the power in the fundamental frequency S to power of the largest spurious signal R regardless of where it falls in the frequency spectrum. The worst spurious signal might or might not be a harmonic of the original signal. SFDR represents the smallest value of a signal that can be distinguished from a large interfering signal. SFDR includes harmonics.
The harmonic distortion measurement automatically locates the largest sinusoidal component (fundamental signal frequency). It then computes the harmonic frequencies and power in each harmonic in your signal and ignores any DC component. The measurement does not include any harmonics that are outside the Spectrum Analyzer frequency span. Adjust your frequency span so that it includes all the desired harmonics.
Note
To view the best harmonics, make sure that your fundamental frequency is set high enough to resolve the harmonics. However, this frequency should not be so high that aliasing occurs. For the best display of harmonic distortion, your plot should not show skirts, which indicate frequency leakage. The noise floor should be visible.
For a better display, try a Kaiser window with a large sidelobe attenuation (e.g. between 100–300 db).
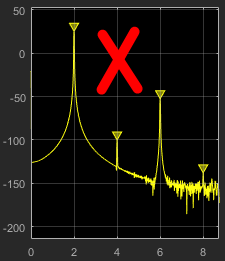
When you set the Distortion Type to
Intermodulation, the following fields appear in the
Intermodulation Distortion panel at the bottom of the Spectrum
Analyzer window.
F1 — Lower fundamental first-order frequency.
F2 — Upper fundamental first-order frequency.
2F1 - F2 — Lower intermodulation product from third-order harmonics.
2F2 - F1 — Upper intermodulation product from third-order harmonics.
TOI — Third-order intercept point. If the noise power is too high in relation to the harmonics, the TOI value will not be accurate. In this case, you should lower the resolution bandwidth or select a different spectral window. If the TOI has the same amplitude as the input two-tone signal, reduce the power of that input signal.
The intermodulation distortion measurement automatically locates the fundamental and the first-order frequencies (F1 and F2). It then computes the frequencies of the third-order intermodulation products (2F1−F2 and 2F2−F1).
For modifying the distortion measurements programmatically, see the DistortionMeasurementsConfiguration object. For more information on these
settings in the UI, see Distortion.
Set configuration and style settings in the Spectrum Analyzer.
To control the settings of the display and labels, color and styling, click on
Settings (![]() ) in the Scope tab of the Spectrum
Analyzer toolstrip.
) in the Scope tab of the Spectrum
Analyzer toolstrip.
In the dialog box that opens, you can customize the font size, plot type, y-axis properties of the spectrum plot, and color map properties of the spectrogram plot. You can change the color of the spectrum plot, background, axes, and labels and also change the line properties.
When you view the spectrum or the spectrogram, you see only the relevant options. For more details about these options, see Configuration > Spectrum Analyzer Settings.
Zoom and pan axes using display controls.
To scale the plot axes, use the mouse to pan around the axes and the scroll button on your mouse to zoom in and out of the plot. Additionally, you can use the buttons that appear when you hover over the plot window.
 — Maximize the axes, hide all labels and inset
the axes values.
— Maximize the axes, hide all labels and inset
the axes values. — Zoom in on the plot.
— Zoom in on the plot. — Pan the plot.
— Pan the plot. — Autoscale the axes to fit the shown data.
— Autoscale the axes to fit the shown data.
Tips
If you set the Averaging Method to VBW or
Exponential, and you introduce NaN or
Inf values into the data, the spectrum appears blank. To ignore the
NaN or Inf values:
In the Home tab > Environment section of the MATLAB® toolstrip, click Settings (
 ).
).In the Workspace section of the Settings dialog box, select the Ignore NaNs when calculating statistics check box.
Algorithms
When you select the Welch method, the power spectrum estimate is
the averaged modified periodograms.
The algorithm in the spectrum analyzer consists of these steps:
The block buffers the input into N-point data segments. Each data segment is split into P overlapping data segments, each of length M, overlapping by D points. The data segments can be represented as:
If D = M/2, the overlap is 50%.
If D = 0, the overlap is 0%.
Apply a window to each of the P overlapping data segments in the time domain.
The spectrum analyzer uses RBW (Hz) in the Estimation tab to determine the data window length internally.
Then, it partitions the input signal into a number of windowed data segments.
Most window functions afford more influence to the data at the center of the set than to the data at the edges, which represents a loss of information. To mitigate that loss, the individual data sets are commonly overlapped in time. For each windowed segment, compute the periodogram by computing the discrete Fourier transform. Then compute the squared magnitude of the result and divide the result by M.
where U is the normalization factor for the power in the window function and is given by
You can specify the window using the Window parameter in the Estimation tab of the spectrum analyzer toolstrip.
The spectrum analyzer calculates and plots the power spectrum, power spectrum density, and RMS using the modified Periodogram estimator. For more information about the Periodogram method, see
periodogram(Signal Processing Toolbox).To determine the power spectrum estimate for Welch's method, the spectrum analyzer averages the result of the periodograms for the last P data segments. The averaging reduces the variance, compared to the original N-point data segment. For more details on the averaging, see Averaging Method.
The spectrum analyzer computes the power spectral density using:
The power spectrum is the product of the power spectral density and the resolution bandwidth, as given by this equation.
The spectrum analyzer uses a certain number of samples to compute a spectral estimate. This value is directly related to the resolution bandwidth (RBW) using this equation,
where Op is the overlap percentage, NENBW is the normalized effective noise bandwidth, Fs is the input sample rate, and RBW is the resolution bandwidth.
The spectrum analyzer shows the number of samples per update in the spectrum analyzer status bar.
The algorithm determines the window length using this equation:
The overlap percentage Op is the value you specify in the Overlap % property. To view the Overlap % in the scope, click the Estimation tab on the spectrum analyzer toolstrip and navigate to the Window Options section.
When you increase the overlap percentage, the spectrum analyzer needs fewer new input samples to compute a new spectral update.
| Op | Nsamples |
|---|---|
| 0% | 100 |
| 50% | 50 |
| 80% | 20 |
The normalized effective noise bandwidth NENBW is a window parameter that measures the noise performance of the window. NENBW is determined using the window length and the window coefficients, and is given by the following equation:
w(n) denotes the vector of window coefficients. Nwindow is the window length. For more information on how the algorithm determines the window length, see the Spectrum Estimation –– Welch's Method section in Algorithms.
The rectangular window has the smallest NENBW, with a value of 1. All other windows have a larger NENBW value. For example, the Hann window has an NENBW value of approximately 1.5.
The spectrum analyzer shows the value of NENBW in the spectrum analyzer status bar.
Fs is the sample rate of the input signal.
To view the Sample Rate (Hz) in the scope, click the
Scope tab on the spectrum analyzer toolstrip and navigate to
the Bandwidth section. You can enable this property in the status
bar at the bottom of the spectrum analyzer window. Click the ![]() icon in the status bar and select
icon in the status bar and select Sample
Rate.
Resolution bandwidth controls the spectral resolution of the displayed signal. The RBW value determines the spacing between frequencies that the scope can resolve. A smaller value gives a higher spectral resolution and lowers the noise floor, that is, the spectrum analyzer can resolve frequencies that are closer to each other. However, this comes at the cost of a longer sweep time.
You can specify the resolution bandwidth using the RBW (Hz) parameter.
When you set RBW (Hz) to:
Auto–– The spectrum analyzer determines the appropriate resolution bandwidth to ensure that there are 1024 RBW intervals over the specified frequency span. When you set RBW (Hz) toAuto, the spectrum analyzer calculates using this equation.scalar value –– Specify a value such that there are at least two RBW intervals over the specified frequency span. The ratio of the overall span to RBW must be greater than two:
span is the frequency span over which the spectrum analyzer
computes and plots the spectrum. Spectrum analyzer shows the span through the
Span (Hz) property. To view the Span (Hz)
in the scope, click the Estimation tab on the spectrum analyzer
toolstrip, navigate to the Frequency Options section, and set
Frequency Span to Span and Center
Frequency.
When the number of input samples is not sufficient to achieve the specified resolution bandwidth, the spectrum analyzer adjusts its RBW value according to the number of input samples provided and displays a message similar to this one. The spectrum analyzer removes this message once you provide enough input samples.

You can enable this property in the status bar at the bottom of the spectrum analyzer
window. Click the ![]() icon in the status bar and select
icon in the status bar and select
RBW.
When you plot the two-sided spectrum by selecting Two-Sided Spectrum in the Spectrum tab, the Nyquist frequency interval is Hz.
When you clear the Two-Sided Spectrum, the Nyquist frequency interval is Hz.
When you set Frequency (Hz) to Auto, the software calculates the frequency vector for the frequency-domain input.
When you plot the two-sided spectrum by selecting Two-Sided Spectrum in the Spectrum or Spectrogram tab, the frequency vector is:
When you clear the Two-Sided Spectrum, the frequency vector is:
The spectrum analyzer calculates Occupied BW using these steps.
Calculate the total power in the measured frequency range.
Determine the lower frequency value. Starting at the lowest frequency in the range and moving upward, sum the power distributed in each frequency until the result is
of the total power.
Determine the upper frequency value. Starting at the highest frequency in the range and moving downward, sum the power distributed in each frequency until the result reaches
of the total power.
The bandwidth between the lower and upper power frequency values is the occupied bandwidth.
The frequency halfway between the lower and upper frequency values is the center frequency.
The spectrum analyzer calculates Distortion Measurements using these steps.
Estimate spectral content by finding peaks in the spectrum. When the algorithm detects a peak, it records the width of the peak and clears all monotonically decreasing values by treating all these values as if they belong to the peak. Using this method, the algorithm removes all spectral content centered at DC (0 Hz) from the spectrum and records the amount of bandwidth cleared (W0).
Determine the fundamental power (P1) from the remaining maximum value of the displayed spectrum. Create a local estimate (Fe1) of the fundamental frequency by computing the central moment of the power near the peak. Record the bandwidth of the fundamental power content (W1). Then remove the power from the fundamental as in step 1.
Determine the power and width of the higher-order harmonics (P2, W2, P3, W3, etc.) in succession by examining the frequencies closest to the appropriate multiple of the local estimate (Fe1). Remove any spectral content that decreases monotonically about the harmonic frequency from the spectrum before proceeding to the next harmonic.
After removing the DC, fundamental, and harmonic content from the spectrum, examine the power of the remaining spectrum for its sum (Premaining), peak value (Pmaxspur), and median value (Pestnoise).
Compute the sum of all the removed bandwidth as Wsum = W0 + W1 + W2 +...+ Wn.
Compute the sum of powers of the second and higher-order harmonics as Pharmonic = P2 + P3 + P4 +...+ Pn.
Estimate the sum of the noise power as:
Where dF is the absolute difference between frequency bins, and RBW is the resolution bandwidth of the window.
Then compute the metrics for THD, THD%, SINAD, SNR, and SFDR from the estimates.
The harmonic distortion measurements use the spectrum trace shown in the display as the input to the measurements. The default
Hannwindow setting of the spectrum analyzer might exhibit leakage that can completely mask the noise floor of the measured signal.The harmonic measurements attempt to correct for leakage by ignoring all frequency content that decreases monotonically away from the maximum of harmonic peaks. If the window leakage covers more than 70% of the frequency bandwidth in your spectrum, you may see a blank reading (–) reported for SNR and SINAD. If your application can tolerate the increased equivalent noise bandwidth (ENBW), consider using a Kaiser window with a high attenuation (up to 330 dB) to minimize spectral leakage.
Ignore the DC component.
After windowing, the width of each harmonic component masks the noise power in the neighborhood of the fundamental frequency and harmonics. To estimate the noise power in each region, the spectrum analyzer computes the median noise level in the nonharmonic areas of the spectrum. It then extrapolates that value into each region.
Nth order intermodulation products occur at A*F1 + B*F2,
where F1 and F2 are the sinusoid input frequencies and |A| + |B| = N. A and B are integer values.
For intermodulation measurements, compute the third-order intercept (TOI) point as follows.
TOIlower = PF1 + (PF2 - P(2F1-F2))/2
TOIupper = PF2 + (PF1 - P(2F2-F1))/2
TOI = + (TOIlower + TOIupper)/2
Where P is power in decibels of the measured power referenced to 1 milliwatt (dBm).
The spectrum analyzer calculates the moving average using one of these methods:
Video bandwidth — The spectrum analyzer uses a time-domain lowpass filter to smooth the noise in the signal. The video bandwidth (VBW) filter smoothes the trace and decreases noise, and the spectrum analyzer applies the filter to the data before displaying it.
Video bandwidth is the bandwidth of the lowpass filter that spectrum analyzer uses to average or smooth the noise in the signal before displaying it in the scope. The spectrum analyzer computes the video bandwidth using this equation:
where,
Video bandwidth does not affect the level of the noise (noise floor), but only increases the signal-to-noise ratio and smoothes the trace of the noise. When you decrease the value of VBW, the signal-to-noise ratio improves.
The cutoff frequency of the video bandwidth filter is given by:
where Fs is the input sample rate and NFFT is the number of FFT points.
The spectrum analyzer shows the values of sample rate, VBW, and NFFT in the status bar at the bottom of the display. To enable, right-click the status bar and select
Sample Rate,VBW, andNFFT.Exponential — The moving average algorithm uses the exponential weighting method to update the weights and compute the moving average recursively for each Z vector that comes in by using the following recursive equations:
λ — Forgetting factor
— Weighting factor applied to the current Z vector
— Current Z vector
— Moving average until the previous Z vector
— Effect of the previous Z vectors on the average
— Moving average including the current Z vector
Running –– For each frame of the input, average the last Q scaled Z vectors, which are computed by the algorithm. The variable Q is the value you specify for the number of spectral averages. If the algorithm does not have enough Z vectors, the algorithm uses zeros to fill the empty elements.
Extended Capabilities
This block can be used for simulation visibility in systems that generate code. However, the block is not included in the generated code.
Version History
Introduced in R2017bYou can now individually control the type of plot for each line. To control the type of plot for a line, select the line and set the Plot Type parameter accordingly.
The Spectrum Analyzer block now supports the running averaging method to
compute the power spectrum estimate. To enable this mode, set the Averaging
Method parameter in the Estimation tab to
Running and the Spectral Averages
parameter to a positive integer.
For more information, see the Algorithms section.
Previously, the Spectrum Analyzer block required a minimum number of samples to update the display for a given RBW value. Starting in R2024b, this limitation is removed. The scope now updates its display for any number of input samples and adjusts the RBW value accordingly.
The Spectrum Analyzer block can now automatically adjust the resolution bandwidth (RBW) so as to maintain the number of samples per spectral update at 1024 (Nsamples = 1024) irrespective of the window you select.
To enable this mode in the Spectrum Analyzer block, set:
RBW (Hz) to
Auto.
You can now increase the display precision to 15 digits using the Display Precision property in the scope settings under Display and Labels. This precision affects all the measurements and data that the scope displays on its status bar.
The Preserve colors for copy to clipboard property has been renamed to Preserve Colors and is now available in the scope toolstrip under Copy Display.
The Analyzer tab in spectrum analyzer has been renamed as Scope tab.
You can set Spectrum Unit to dBuV when
you set Spectrum to RMS.
In R2023a, the Spectrum Analyzer block is more responsive and its
toolstrip interface is improved to provide you easy access to spectral analysis, estimation,
and measurements. You can configure and display Spectrum Analyzer settings from the command
line with the SpectrumAnalyzerBlockConfiguration object.
See Also
Objects
SpectrumAnalyzerBlockConfiguration|spectrumAnalyzer(DSP System Toolbox)
Blocks
- Spectrum Analyzer (DSP System Toolbox)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)