Binomial Distribution
Overview
The binomial distribution is a two-parameter family of curves. The binomial distribution is used to model the total number of successes in a fixed number of independent trials that have the same probability of success, such as modeling the probability of a given number of heads in ten flips of a fair coin.
Statistics and Machine Learning Toolbox™ offers several ways to work with the binomial distribution.
Create a probability distribution object
BinomialDistributionby fitting a probability distribution to sample data (fitdist) or by specifying parameter values (makedist). Then, use object functions to evaluate the distribution, generate random numbers, and so on.Work with the binomial distribution interactively by using the Distribution Fitter app. You can export an object from the app and use the object functions.
Use distribution-specific functions (
binocdf,binopdf,binoinv,binostat,binofit,binornd) with specified distribution parameters. The distribution-specific functions can accept parameters of multiple binomial distributions.Use generic distribution functions (
cdf,icdf,pdf,random) with a specified distribution name ('Binomial') and parameters.
Parameters
The binomial distribution uses the following parameters.
| Parameter | Description | Support |
|---|---|---|
| N | Number of trials | Positive integer |
| p | Probability of success in a single trial |
The sum of two binomial random variables that both have the same parameter p is also a binomial random variable with N equal to the sum of the number of trials.
Probability Density Function
The probability density function (pdf) of the binomial distribution is
where x is the number of successes in N trials of a Bernoulli process with the probability of success p. The result is the probability of exactly x successes in N trials. For discrete distributions, the pdf is also known as the probability mass function (pmf).
For an example, see Compute Binomial Distribution pdf.
Cumulative Distribution Function
The cumulative distribution function (cdf) of the binomial distribution is
where x is the number of successes in N trials of a Bernoulli process with the probability of success p. The result is the probability of at most x successes in N trials.
For an example, see Compute Binomial Distribution cdf.
Descriptive Statistics
The mean of the binomial distribution is Np.
The variance of the binomial distribution is Np(1 – p).
Example
Fit Binomial Distribution to Data
Generate a binomial random number that counts the number of successes in 100 trials with the probability of success 0.9 in each trial.
x = binornd(100,0.9)
x = 85
Fit a binomial distribution to data using fitdist.
pd = fitdist(x,'Binomial','NTrials',100)
pd =
BinomialDistribution
Binomial distribution
N = 100
p = 0.85 [0.764692, 0.913546]
fitdist returns a BinomialDistribution object. The interval next to p is the 95% confidence interval estimating p.
Estimate the parameter p using the distribution functions.
[phat,pci] = binofit(x,100) % Distribution-specific functionphat = 0.8500
pci = 1×2
0.7647 0.9135
[phat2,pci2] = mle(x,'distribution','Binomial',"NTrials",100) % Generic distribution function
phat2 = 0.8500
pci2 = 2×1
0.7647
0.9135
Compute Binomial Distribution pdf
Compute the pdf of the binomial distribution with 10 trials and the probability of success 0.5.
x = 0:10; y = binopdf(x,10,0.5);
Plot the pdf with bars of width 1.
figure bar(x,y,1) xlabel('Observation') ylabel('Probability')
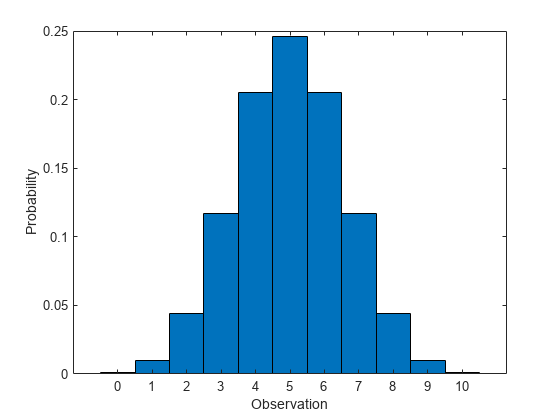
Compute Binomial Distribution cdf
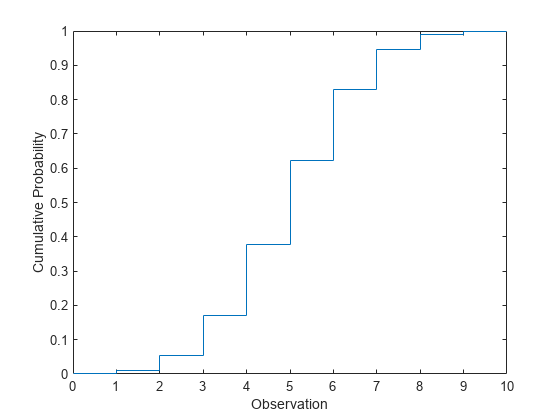
Compute the cdf of the binomial distribution with 10 trials and the probability of success 0.5.
x = 0:10; y = binocdf(x,10,0.5);
Plot the cdf.
figure stairs(x,y) xlabel('Observation') ylabel('Cumulative Probability')
Compare Binomial and Normal Distribution pdfs
When N is large, the binomial distribution with parameters N and p can be approximated by the normal distribution with mean N*p and variance N*p*(1–p) provided that p is not too large or too small.
Compute the pdf of the binomial distribution counting the number of successes in 50 trials with the probability 0.6 in a single trial.
N = 50; p = 0.6; x1 = 0:N; y1 = binopdf(x1,N,p);
Compute the pdf of the corresponding normal distribution.
mu = N*p; sigma = sqrt(N*p*(1-p)); x2 = 0:0.1:N; y2 = normpdf(x2,mu,sigma);
Plot the pdfs on the same axis.
figure bar(x1,y1,1) hold on plot(x2,y2,'LineWidth',2) xlabel('Observation') ylabel('Probability') title('Binomial and Normal pdfs') legend('Binomial Distribution','Normal Distribution','location','northwest') hold off
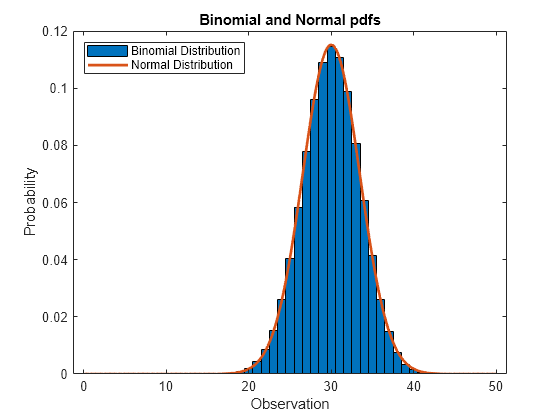
The pdf of the normal distribution closely approximates the pdf of the binomial distribution.
Compare Binomial and Poisson Distribution pdfs
When p is small, the binomial distribution with parameters N and p can be approximated by the Poisson distribution with mean N*p, provided that N*p is also small.
Compute the pdf of the binomial distribution counting the number of successes in 20 trials with the probability of success 0.05 in a single trial.
N = 20; p = 0.05; x = 0:N; y1 = binopdf(x,N,p);
Compute the pdf of the corresponding Poisson distribution.
mu = N*p; y2 = poisspdf(x,mu);
Plot the pdfs on the same axis.
figure bar(x,[y1; y2]) xlabel('Observation') ylabel('Probability') title('Binomial and Poisson pdfs') legend('Binomial Distribution','Poisson Distribution','location','northeast')
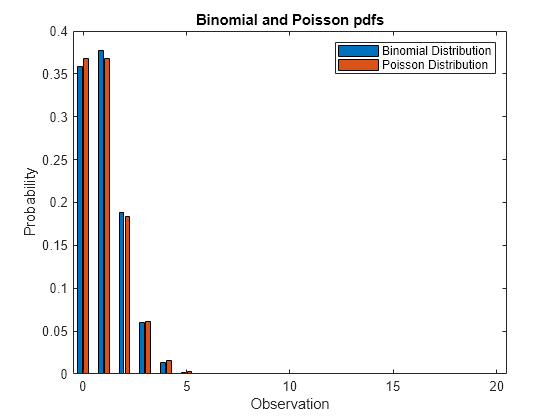
The pdf of the Poisson distribution closely approximates the pdf of the binomial distribution.
Related Distributions
Bernoulli Distribution — The Bernoulli distribution is a one-parameter discrete distribution that models the success of a single trial, and occurs as a binomial distribution with N = 1.
Multinomial Distribution — The multinomial distribution is a discrete distribution that generalizes the binomial distribution when each trial has more than two possible outcomes.
Normal Distribution — The normal distribution is a two-parameter continuous distribution that has parameters μ (mean) and σ (standard deviation). As N increases, the binomial distribution can be approximated by a normal distribution with µ = Np and σ2 = Np(1 – p). See Compare Binomial and Normal Distribution pdfs.
Poisson Distribution — The Poisson distribution is a one-parameter discrete distribution that takes nonnegative integer values. The parameter λ is both the mean and the variance of the distribution. The Poisson distribution is the limiting case of a binomial distribution where N approaches infinity and p goes to zero while Np = λ. See Compare Binomial and Poisson Distribution pdfs.
References
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.
[3] Loader, Catherine. Fast and Accurate Computation of Binomial Probabilities. July 9, 2000.
See Also
BinomialDistribution | binocdf | binopdf | binoinv | binostat | binofit | binornd | makedist | fitdist