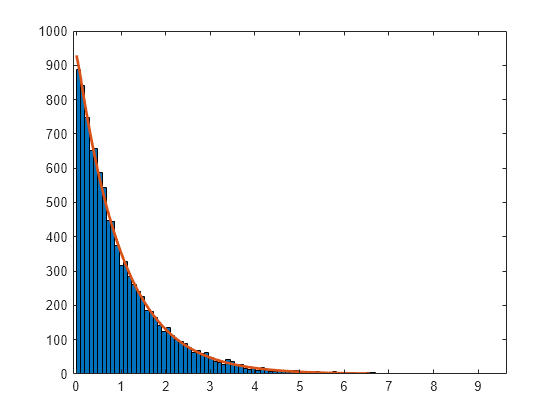
random
Random numbers
Syntax
Description
R = random(___,sz1,...,szN)sz1,...,szN indicates the size of each
dimension.
Examples
Input Arguments
Output Arguments
Alternative Functionality
randomis a generic function that accepts either a distribution by its namenameor a probability distribution objectpd. It is faster to use a distribution-specific function, such asrandnandnormrndfor the normal distribution andbinorndfor the binomial distribution. For a list of distribution-specific functions, see Supported Distributions.To generate random numbers interactively, use
randtool, a user interface for random number generation.