plot
Plot clustering evaluation object criterion values
Description
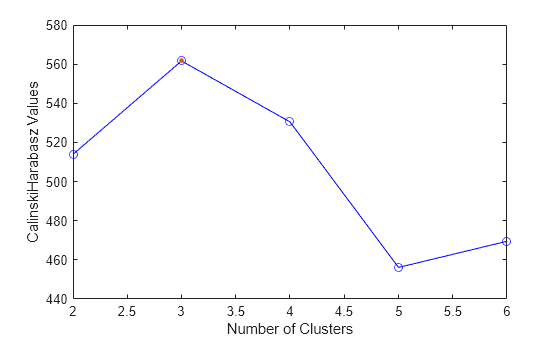
plot( displays a plot of the
criterion values versus the number of clusters, based on the values in the clustering
evaluation object evaluation)evaluation.
plot( plots
into the axes specified by ax,evaluation)ax instead of the current axes (gca). (since R2024a)
h = plot(___)Line object using any of the input argument combinations in the previous
syntaxes. Use this object to inspect and adjust the properties of the plot line. For a list
of properties, see Line Properties.