fsrnca
Feature selection using neighborhood component analysis for regression
Syntax
Description
fsrnca performs feature selection using neighborhood
component analysis (NCA) for regression.
To perform NCA-based feature selection for classification, see fscnca.
mdl = fsrnca(Tbl,ResponseVarName)Tbl. ResponseVarName is the name of
the variable in Tbl that contains the response values.
fsrnca learns the feature weights by using a diagonal
adaptation of NCA with regularization.
mdl = fsrnca(X,Y,Name,Value)
Examples
Generate toy data where the response variable depends on the 3rd, 9th, and 15th predictors.
rng(0,'twister'); % For reproducibility N = 100; X = rand(N,20); y = 1 + X(:,3)*5 + sin(X(:,9)./X(:,15) + 0.25*randn(N,1));
Fit the neighborhood component analysis model for regression.
mdl = fsrnca(X,y,'Verbose',1,'Lambda',0.5/N);
o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 0 | 1.636932e+00 | 3.688e-01 | 0.000e+00 | | 1.627e+00 | 0.000e+00 | YES |
| 1 | 8.304833e-01 | 1.083e-01 | 2.449e+00 | OK | 9.194e+00 | 4.000e+00 | YES |
| 2 | 7.548105e-01 | 1.341e-02 | 1.164e+00 | OK | 1.095e+01 | 1.000e+00 | YES |
| 3 | 7.346997e-01 | 9.752e-03 | 6.383e-01 | OK | 2.979e+01 | 1.000e+00 | YES |
| 4 | 7.053407e-01 | 1.605e-02 | 1.712e+00 | OK | 5.809e+01 | 1.000e+00 | YES |
| 5 | 6.970502e-01 | 9.106e-03 | 8.818e-01 | OK | 6.223e+01 | 1.000e+00 | YES |
| 6 | 6.952347e-01 | 5.522e-03 | 6.382e-01 | OK | 3.280e+01 | 1.000e+00 | YES |
| 7 | 6.946302e-01 | 9.102e-04 | 1.952e-01 | OK | 3.380e+01 | 1.000e+00 | YES |
| 8 | 6.945037e-01 | 6.557e-04 | 9.942e-02 | OK | 8.490e+01 | 1.000e+00 | YES |
| 9 | 6.943908e-01 | 1.997e-04 | 1.756e-01 | OK | 1.124e+02 | 1.000e+00 | YES |
| 10 | 6.943785e-01 | 3.478e-04 | 7.755e-02 | OK | 7.621e+01 | 1.000e+00 | YES |
| 11 | 6.943728e-01 | 1.428e-04 | 3.416e-02 | OK | 3.649e+01 | 1.000e+00 | YES |
| 12 | 6.943711e-01 | 1.128e-04 | 1.231e-02 | OK | 6.092e+01 | 1.000e+00 | YES |
| 13 | 6.943688e-01 | 1.066e-04 | 2.326e-02 | OK | 9.319e+01 | 1.000e+00 | YES |
| 14 | 6.943655e-01 | 9.324e-05 | 4.399e-02 | OK | 1.810e+02 | 1.000e+00 | YES |
| 15 | 6.943603e-01 | 1.206e-04 | 8.823e-02 | OK | 4.609e+02 | 1.000e+00 | YES |
| 16 | 6.943582e-01 | 1.701e-04 | 6.669e-02 | OK | 8.425e+01 | 5.000e-01 | YES |
| 17 | 6.943552e-01 | 5.160e-05 | 6.473e-02 | OK | 8.832e+01 | 1.000e+00 | YES |
| 18 | 6.943546e-01 | 2.477e-05 | 1.215e-02 | OK | 7.925e+01 | 1.000e+00 | YES |
| 19 | 6.943546e-01 | 1.077e-05 | 6.086e-03 | OK | 1.378e+02 | 1.000e+00 | YES |
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 20 | 6.943545e-01 | 2.260e-05 | 4.071e-03 | OK | 5.856e+01 | 1.000e+00 | YES |
| 21 | 6.943545e-01 | 4.250e-06 | 1.109e-03 | OK | 2.964e+01 | 1.000e+00 | YES |
| 22 | 6.943545e-01 | 1.916e-06 | 8.356e-04 | OK | 8.649e+01 | 1.000e+00 | YES |
| 23 | 6.943545e-01 | 1.083e-06 | 5.270e-04 | OK | 1.168e+02 | 1.000e+00 | YES |
| 24 | 6.943545e-01 | 1.791e-06 | 2.673e-04 | OK | 4.016e+01 | 1.000e+00 | YES |
| 25 | 6.943545e-01 | 2.596e-07 | 1.111e-04 | OK | 3.154e+01 | 1.000e+00 | YES |
Infinity norm of the final gradient = 2.596e-07
Two norm of the final step = 1.111e-04, TolX = 1.000e-06
Relative infinity norm of the final gradient = 2.596e-07, TolFun = 1.000e-06
EXIT: Local minimum found.
Plot the selected features. The weights of the irrelevant features should be close to zero.
figure() plot(mdl.FeatureWeights,'ro') grid on xlabel('Feature index') ylabel('Feature weight')

fsrnca correctly detects the relevant predictors for this response.
Load the sample data.
load robotarm.matThe robotarm (pumadyn32nm) dataset is created using a robot arm simulator with 7168 training observations and 1024 test observations with 32 features [1][2]. This is a preprocessed version of the original data set. The data are preprocessed by subtracting off a linear regression fit, followed by normalization of all features to unit variance.
Perform neighborhood component analysis (NCA) feature selection for regression with the default (regularization parameter) value.
nca = fsrnca(Xtrain,ytrain,'FitMethod','exact', ... 'Solver','lbfgs');
Plot the selected values.
figure plot(nca.FeatureWeights,'ro') xlabel('Feature index') ylabel('Feature weight') grid on
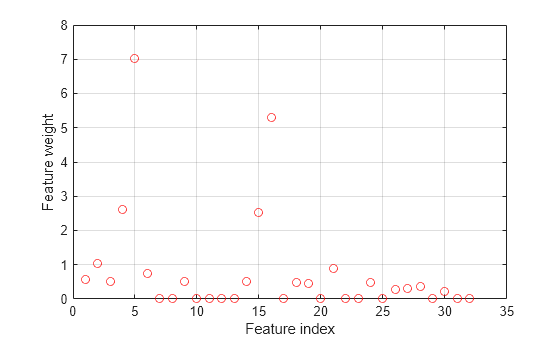
More than half of the feature weights are nonzero. Compute the loss using the test set as a measure of the performance by using the selected features.
L = loss(nca,Xtest,ytest)
L = 0.0837
Try improving the performance. Tune the regularization parameter for feature selection using five-fold cross-validation. Tuning means finding the value that produces the minimum regression loss. To tune using cross-validation:
1. Partition the data into five folds. For each fold, cvpartition assigns 4/5th of the data as a training set, and 1/5th of the data as a test set.
rng(1) % For reproducibility n = length(ytrain); cvp = cvpartition(length(ytrain),'kfold',5); numvalidsets = cvp.NumTestSets;
Assign the values for the search. Multiplying response values by a constant increases the loss function term by a factor of the constant. Therefore, including the std(ytrain) factor in the values balances the default loss function ('mad', mean absolute deviation) term and the regularization term in the objective function. In this example, the std(ytrain) factor is one because the loaded sample data is a preprocessed version of the original data set.
lambdavals = linspace(0,50,20)*std(ytrain)/n;
Create an array to store the loss values.
lossvals = zeros(length(lambdavals),numvalidsets);
2. Train the NCA model for each value, using the training set in each fold.
3. Compute the regression loss for the corresponding test set in the fold using the NCA model. Record the loss value.
4. Repeat this for each value and each fold.
for i = 1:length(lambdavals) for k = 1:numvalidsets X = Xtrain(cvp.training(k),:); y = ytrain(cvp.training(k),:); Xvalid = Xtrain(cvp.test(k),:); yvalid = ytrain(cvp.test(k),:); nca = fsrnca(X,y,'FitMethod','exact', ... 'Solver','minibatch-lbfgs','Lambda',lambdavals(i), ... 'GradientTolerance',1e-4,'IterationLimit',30); lossvals(i,k) = loss(nca,Xvalid,yvalid,'LossFunction','mse'); end end
Compute the average loss obtained from the folds for each value.
meanloss = mean(lossvals,2);
Plot the mean loss versus the values.
figure plot(lambdavals,meanloss,'ro-') xlabel('Lambda') ylabel('Loss (MSE)') grid on
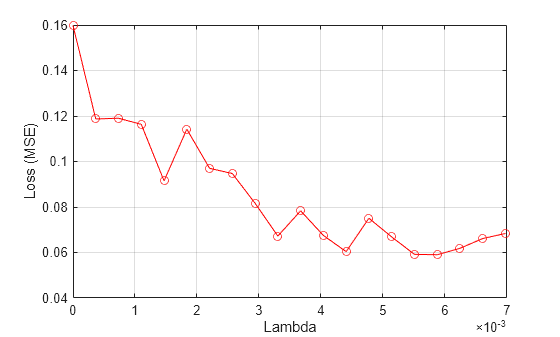
Find the value that gives the minimum loss value.
[~,idx] = min(meanloss)
idx = 17
bestlambda = lambdavals(idx)
bestlambda = 0.0059
bestloss = meanloss(idx)
bestloss = 0.0590
Fit the NCA feature selection model for regression using the best value.
nca = fsrnca(Xtrain,ytrain,'FitMethod','exact', ... 'Solver','lbfgs','Lambda',bestlambda);
Plot the selected features.
figure plot(nca.FeatureWeights,'ro') xlabel('Feature Index') ylabel('Feature Weight') grid on
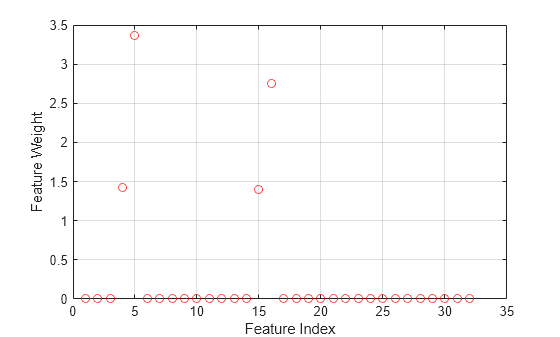
Most of the feature weights are zero. fsrnca identifies the four most relevant features.
Compute the loss for the test set.
L = loss(nca,Xtest,ytest)
L = 0.0571
Tuning the regularization parameter, , eliminated more of the irrelevant features and improved the performance.
This example uses the Abalone data [3][4] from the UCI Machine Learning Repository [5].
Download the data and save it in your current folder with the name 'abalone.csv'.
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data'; websave('abalone.csv',url);
Read the data into a table. Display the first seven rows.
tbl = readtable('abalone.csv','Filetype','text','ReadVariableNames',false); tbl.Properties.VariableNames = {'Sex','Length','Diameter','Height', ... 'WWeight','SWeight','VWeight','ShWeight','NoShellRings'}; tbl(1:7,:)
ans=7×9 table
Sex Length Diameter Height WWeight SWeight VWeight ShWeight NoShellRings
_____ ______ ________ ______ _______ _______ _______ ________ ____________
{'M'} 0.455 0.365 0.095 0.514 0.2245 0.101 0.15 15
{'M'} 0.35 0.265 0.09 0.2255 0.0995 0.0485 0.07 7
{'F'} 0.53 0.42 0.135 0.677 0.2565 0.1415 0.21 9
{'M'} 0.44 0.365 0.125 0.516 0.2155 0.114 0.155 10
{'I'} 0.33 0.255 0.08 0.205 0.0895 0.0395 0.055 7
{'I'} 0.425 0.3 0.095 0.3515 0.141 0.0775 0.12 8
{'F'} 0.53 0.415 0.15 0.7775 0.237 0.1415 0.33 20
The dataset has 4177 observations. The goal is to predict the age of abalone from eight physical measurements. The last variable, the number of shell rings, shows the age of the abalone. The first predictor is a categorical variable. The last variable in the table is the response variable.
Prepare the predictor and response variables for fsrnca. The last column of tbl contains the number of shell rings, which is the response variable. The first predictor variable, sex, is categorical. You must create dummy variables.
y = table2array(tbl(:,end)); X(:,1:3) = dummyvar(categorical(tbl.Sex)); X = [X,table2array(tbl(:,2:end-1))];
Use four-fold cross-validation to tune the regularization parameter in the NCA model. First partition the data into four folds.
rng('default') % For reproducibility n = length(y); cvp = cvpartition(n,'kfold',4); numtestsets = cvp.NumTestSets;
cvpartition divides the data into four partitions (folds). In each fold, about three-fourths of the data is assigned as a training set and one-fourth is assigned as a test set.
Generate a variety of (regularization parameter) values for fitting the model to determine the best value. Create a vector to collect the loss values from each fit.
lambdavals = linspace(0,25,20)*std(y)/n; lossvals = zeros(length(lambdavals),numtestsets);
The rows of lossvals corresponds to the values and the columns correspond to the folds.
Fit the NCA model for regression using fsrnca to the data from each fold using each value. Compute the loss for each model using the test data from each fold.
for i = 1:length(lambdavals) for k = 1:numtestsets Xtrain = X(cvp.training(k),:); ytrain = y(cvp.training(k),:); Xtest = X(cvp.test(k),:); ytest = y(cvp.test(k),:); nca = fsrnca(Xtrain,ytrain,'FitMethod','exact', ... 'Solver','lbfgs','Lambda',lambdavals(i),'Standardize',true); lossvals(i,k) = loss(nca,Xtest,ytest,'LossFunction','mse'); end end
Compute the average loss for the folds, that is, compute the mean in the second dimension of lossvals.
meanloss = mean(lossvals,2);
Plot the values versus the mean loss from the four folds.
figure plot(lambdavals,meanloss,'ro-') xlabel('Lambda') ylabel('Loss (MSE)') grid on

Find the value that minimizes the mean loss.
[~,idx] = min(meanloss); bestlambda = lambdavals(idx)
bestlambda = 0.0071
Compute the best loss value.
bestloss = meanloss(idx)
bestloss = 4.7799
Fit the NCA model on all of the data using the best value.
nca = fsrnca(X,y,'FitMethod','exact','Solver','lbfgs', ... 'Verbose',1,'Lambda',bestlambda,'Standardize',true);
o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 0 | 2.469168e+00 | 1.266e-01 | 0.000e+00 | | 4.741e+00 | 0.000e+00 | YES |
| 1 | 2.375166e+00 | 8.265e-02 | 7.268e-01 | OK | 1.054e+01 | 1.000e+00 | YES |
| 2 | 2.293528e+00 | 2.067e-02 | 2.034e+00 | OK | 1.569e+01 | 1.000e+00 | YES |
| 3 | 2.286703e+00 | 1.031e-02 | 3.158e-01 | OK | 2.213e+01 | 1.000e+00 | YES |
| 4 | 2.279928e+00 | 2.023e-02 | 9.374e-01 | OK | 1.953e+01 | 1.000e+00 | YES |
| 5 | 2.276258e+00 | 6.884e-03 | 2.497e-01 | OK | 1.439e+01 | 1.000e+00 | YES |
| 6 | 2.274358e+00 | 1.792e-03 | 4.010e-01 | OK | 3.109e+01 | 1.000e+00 | YES |
| 7 | 2.274105e+00 | 2.412e-03 | 2.399e-01 | OK | 3.557e+01 | 1.000e+00 | YES |
| 8 | 2.274073e+00 | 1.459e-03 | 7.684e-02 | OK | 1.356e+01 | 1.000e+00 | YES |
| 9 | 2.274050e+00 | 3.733e-04 | 3.797e-02 | OK | 1.725e+01 | 1.000e+00 | YES |
| 10 | 2.274043e+00 | 2.750e-04 | 1.379e-02 | OK | 2.445e+01 | 1.000e+00 | YES |
| 11 | 2.274027e+00 | 2.682e-04 | 5.701e-02 | OK | 7.386e+01 | 1.000e+00 | YES |
| 12 | 2.274020e+00 | 1.712e-04 | 4.107e-02 | OK | 9.461e+01 | 1.000e+00 | YES |
| 13 | 2.274014e+00 | 2.633e-04 | 6.720e-02 | OK | 7.469e+01 | 1.000e+00 | YES |
| 14 | 2.274012e+00 | 9.818e-05 | 2.263e-02 | OK | 3.275e+01 | 1.000e+00 | YES |
| 15 | 2.274012e+00 | 4.220e-05 | 6.188e-03 | OK | 2.799e+01 | 1.000e+00 | YES |
| 16 | 2.274012e+00 | 2.859e-05 | 4.979e-03 | OK | 6.628e+01 | 1.000e+00 | YES |
| 17 | 2.274011e+00 | 1.582e-05 | 6.767e-03 | OK | 1.439e+02 | 1.000e+00 | YES |
| 18 | 2.274011e+00 | 7.623e-06 | 4.311e-03 | OK | 1.211e+02 | 1.000e+00 | YES |
| 19 | 2.274011e+00 | 3.038e-06 | 2.528e-04 | OK | 1.798e+01 | 5.000e-01 | YES |
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 20 | 2.274011e+00 | 6.710e-07 | 2.325e-04 | OK | 2.721e+01 | 1.000e+00 | YES |
Infinity norm of the final gradient = 6.710e-07
Two norm of the final step = 2.325e-04, TolX = 1.000e-06
Relative infinity norm of the final gradient = 6.710e-07, TolFun = 1.000e-06
EXIT: Local minimum found.
Plot the selected features.
figure plot(nca.FeatureWeights,'ro') xlabel('Feature Index') ylabel('Feature Weight') grid on

The irrelevant features have zero weights. According to this figure, the features 1, 3, and 9 are not selected.
Fit a Gaussian process regression (GPR) model using the subset of regressors method for parameter estimation and the fully independent conditional method for prediction. Use the ARD squared exponential kernel function, which assigns an individual weight to each predictor. Standardize the predictors.
gprMdl = fitrgp(tbl,'NoShellRings','KernelFunction','ardsquaredexponential', ... 'FitMethod','sr','PredictMethod','fic','Standardize',true)
gprMdl =
RegressionGP
PredictorNames: {'Sex' 'Length' 'Diameter' 'Height' 'WWeight' 'SWeight' 'VWeight' 'ShWeight'}
ResponseName: 'NoShellRings'
CategoricalPredictors: 1
ResponseTransform: 'none'
NumObservations: 4177
KernelFunction: 'ARDSquaredExponential'
KernelInformation: [1×1 struct]
BasisFunction: 'Constant'
Beta: 11.4959
Sigma: 2.0282
PredictorLocation: [10×1 double]
PredictorScale: [10×1 double]
Alpha: [1000×1 double]
ActiveSetVectors: [1000×10 double]
PredictMethod: 'FIC'
ActiveSetSize: 1000
FitMethod: 'SR'
ActiveSetMethod: 'Random'
IsActiveSetVector: [4177×1 logical]
LogLikelihood: -9.0019e+03
ActiveSetHistory: [1×1 struct]
BCDInformation: []
Properties, Methods
Compute the regression loss on the training data (resubstitution loss) for the trained model.
L = resubLoss(gprMdl)
L = 4.0306
The smallest cross-validated loss using fsrnca is comparable to the loss obtained using a GPR model with an ARD kernel.
Input Arguments
Sample data used to train the model, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor variable.
Data Types: table
Response variable name, specified as the name of a variable in Tbl. The
remaining variables in the table are predictors.
Data Types: char | string
Explanatory model of the response variable and a subset of the predictor variables, specified
as a string or a character vector in the form "Y~x1+x2+x3". In this
form, Y represents the response variable, and x1,
x2, and x3 represent the predictor
variables.
To specify a subset of variables in Tbl as predictors for training the model, use a formula. If you specify a formula, then the software does not use any variables in Tbl that do not appear in formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl
by using the isvarname function. If the variable
names are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Predictor variable values, specified as an n-by-p matrix, where n is the number of observations and p is the number of predictor variables.
Data Types: single | double
Response values, specified as a numeric real vector of length n, where n is the number of observations.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Solver','sgd','Weights',W,'Lambda',0.0003 specifies the solver as the stochastic gradient descent, the observation weights as the values in the vector W, and sets the regularization parameter at 0.0003.
Fitting Options
Method for fitting the model, specified as the comma-separated
pair consisting of 'FitMethod' and one of the following:
'exact'— Performs fitting using all of the data.'none'— No fitting. Use this option to evaluate the generalization error of the NCA model using the initial feature weights supplied in the call to fsrnca.'average'— Divides the data into partitions (subsets), fits each partition using theexactmethod, and returns the average of the feature weights. You can specify the number of partitions using theNumPartitionsname-value pair argument.
Example: 'FitMethod','none'
Number of partitions to split the data for using with 'FitMethod','average' option,
specified as the comma-separated pair consisting of 'NumPartitions' and
an integer value between 2 and n, where n is
the number of observations.
Example: 'NumPartitions',15
Data Types: double | single
Regularization parameter to prevent overfitting, specified as the comma-separated pair consisting of 'Lambda' and a nonnegative scalar.
As the number of observations n increases, the chance of overfitting decreases and the required amount of regularization also decreases. See Tune Regularization Parameter in NCA for Regression to learn how to tune the regularization parameter.
Example: 'Lambda',0.002
Data Types: double | single
Width of the kernel, specified as the comma-separated pair consisting
of 'LengthScale' and a positive real scalar.
A length scale value of 1 is sensible when all predictors are
on the same scale. If the predictors in X are
of very different magnitudes, then consider standardizing the predictor
values using 'Standardize',true and setting 'LengthScale',1.
Example: 'LengthScale',1.5
Data Types: double | single
Categorical predictors list, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers | Each entry in the vector is an index value corresponding to the column of the predictor data (X) that contains a categorical variable. |
| Logical vector | A true entry means that the corresponding column of predictor data (X) is a categorical variable. |
| Character matrix | Each row of the matrix is the name of a predictor variable in the table X. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable in the table X. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the predictor data is in a table,
fsrnca assumes that a variable is categorical if it is a
logical vector, categorical vector, character array, string array, or cell array of
character vectors. If the predictor data is a matrix, fsrnca
assumes that all predictors are continuous. To identify any other predictors as
categorical predictors, specify them by using the
CategoricalPredictors name-value argument.
For the identified categorical predictors, fsrnca creates dummy variables using two different schemes, depending on whether a categorical variable is unordered or ordered:
For an unordered categorical variable,
fsrncacreates one dummy variable for each level of the categorical variable.For an ordered categorical variable,
fsrncacreates one less dummy variable than the number of categories. For details, see Automatic Creation of Dummy Variables.
For the table X, categorical predictors can be ordered and unordered. For the matrix X, fsrnca treats categorical predictors as unordered.
Example: CategoricalPredictors="all"
Data Types: double | logical | char | string
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
Xas a matrix, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the predictor order inX. That is,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'X1','X2',...}.
If you supply
Xas a table, then you can usePredictorNamesto specify which predictor variables to use in training. That is,fsrncauses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofX.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.Specify the predictors for training using either
PredictorNamesor a formula string inY(such as'y ~ x1 + x2 + x3'), but not both.
Example: "PredictorNames={"SepalLength","SepalWidth","PetalLength","PetalWidth"}
Data Types: string | cell
Response variable name, specified as a character vector or string scalar.
If you supply
Y, then you can useResponseNameto specify a name for the response variable.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: ResponseName="response"
Data Types: char | string
Initial feature weights, specified as an M-by-1 vector of positive numbers,
where M is the number of predictor variables after dummy variables
are created for categorical variables (for details, see
CategoricalPredictors).
The regularized objective function for optimizing feature weights is nonconvex. As a result,
using different initial feature weights might give different results. Setting all
initial feature weights to 1 generally works well, but in some cases, random
initialization using rand(M,1) might give better quality
solutions.
For more information about feature weights, see Neighborhood Component Analysis (NCA) Feature Selection.
Data Types: double | single
Observation weights, specified as the comma-separated pair consisting of
'Weights' and an n-by-1 vector of real
positive scalars. Use observation weights to specify higher importance of some
observations compared to others. The default weights assign equal importance to all
observations.
Data Types: double | single
Indicator for standardizing the predictor data, specified as the comma-separated pair
consisting of 'Standardize' and either false or
true. For more information, see Impact of Standardization.
Example: 'Standardize',true
Data Types: logical
Verbosity level indicator for the convergence summary display,
specified as the comma-separated pair consisting of 'Verbose' and
one of the following:
0 — No convergence summary
1 — Convergence summary, including norm of gradient and objective function values
> 1 — More convergence information, depending on the fitting algorithm
When using
'minibatch-lbfgs'solver and verbosity level > 1, the convergence information includes iteration the log from intermediate mini-batch LBFGS fits.
Example: 'Verbose',1
Data Types: double | single
Solver type for estimating feature weights, specified as the
comma-separated pair consisting of 'Solver' and
one of the following:
'lbfgs'— Limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm'sgd'— Stochastic gradient descent (SGD) algorithm'minibatch-lbfgs'— Stochastic gradient descent with LBFGS algorithm applied to mini-batches
Default is 'lbfgs' for n ≤
1000, and 'sgd' for n > 1000.
Example: 'solver','minibatch-lbfgs'
Loss function, specified as the comma-separated pair consisting of 'LossFunction' and one of the following:
'mad'— Mean absolute deviation'mse'— Mean squared error'epsiloninsensitive'— ε-insensitive loss functionThis loss function is more robust to outliers than mean squared error or mean absolute deviation.
@— Custom loss function handle. A loss function has this form.lossfunfunction L = lossfun(Yu,Yv) % calculation of loss ...
Yuis a u-by-1 vector andYvis a v-by-1 vector.Lis a u-by-v matrix of loss values such thatL(i,j)is the loss value forYu(i)andYv(j).
The objective function for minimization includes the loss function l(yi,yj) as follows:
where w is the feature weight vector, n is the number of observations, and p is the number of predictor variables. pij is the probability that xj is the reference point for xi. For details, see NCA Feature Selection for Regression.
Example: 'LossFunction',@lossfun
Epsilon value for the 'LossFunction','epsiloninsensitive' option, specified as the comma-separated pair consisting of 'LossFunction' and a nonnegative real scalar. The default value is an estimate of the sample standard deviation using the interquartile range of the response variable.
Example: 'Epsilon',0.1
Data Types: double | single
Memory size, in MB, to use for objective function and gradient
computation, specified as the comma-separated pair consisting of 'CacheSize' and
an integer.
Example: 'CacheSize',1500MB
Data Types: double | single
LBFGS Options
Size of history buffer for Hessian approximation for the 'lbfgs' solver,
specified as the comma-separated pair consisting of 'HessianHistorySize' and
a positive integer. At each iteration the function uses the most recent HessianHistorySize iterations
to build an approximation to the inverse Hessian.
Example: 'HessianHistorySize',20
Data Types: double | single
Initial step size for the 'lbfgs' solver,
specified as the comma-separated pair consisting of 'InitialStepSize' and
a positive real scalar. By default, the function determines the initial
step size automatically.
Data Types: double | single
Line search method, specified as the comma-separated pair consisting
of 'LineSearchMethod' and one of the following:
'weakwolfe'— Weak Wolfe line search'strongwolfe'— Strong Wolfe line search'backtracking'— Backtracking line search
Example: 'LineSearchMethod','backtracking'
Maximum number of line search iterations, specified as the comma-separated
pair consisting of 'MaxLineSearchIterations' and
a positive integer.
Example: 'MaxLineSearchIterations',25
Data Types: double | single
Relative convergence tolerance on the gradient norm for solver lbfgs,
specified as the comma-separated pair consisting of 'GradientTolerance' and
a positive real scalar.
Example: 'GradientTolerance',0.000002
Data Types: double | single
SGD Options
Initial learning rate for the 'sgd' solver,
specified as the comma-separated pair consisting of 'InitialLearningRate' and
a positive real scalar.
When using solver type 'sgd', the learning
rate decays over iterations starting with the value specified for 'InitialLearningRate'.
The default 'auto' means that the initial
learning rate is determined using experiments on small subsets of
data. Use the NumTuningIterations name-value
pair argument to specify the number of iterations for automatically
tuning the initial learning rate. Use the TuningSubsetSize name-value
pair argument to specify the number of observations to use for automatically
tuning the initial learning rate.
For solver type 'minibatch-lbfgs', you can
set 'InitialLearningRate' to a very high value.
In this case, the function applies LBFGS to each mini-batch separately
with initial feature weights from the previous mini-batch.
To make sure the chosen initial learning rate decreases the
objective value with each iteration, plot the Iteration versus
the Objective values saved in the mdl.FitInfo property.
You can use the refit method with 'InitialFeatureWeights' equal
to mdl.FeatureWeights to start from the current
solution and run additional iterations
Example: 'InitialLearningRate',0.9
Data Types: double | single
Number of observations to use in each batch for the 'sgd' solver,
specified as the comma-separated pair consisting of 'MiniBatchSize' and
a positive integer from 1 to n.
Example: 'MiniBatchSize',25
Data Types: double | single
Maximum number of passes through all n observations
for solver 'sgd', specified as the comma-separated
pair consisting of 'PassLimit' and a positive integer.
Each pass through all of the data is called an epoch.
Example: 'PassLimit',10
Data Types: double | single
Frequency of batches for displaying convergence summary for
the 'sgd' solver , specified as the comma-separated
pair consisting of 'NumPrint' and a positive integer.
This argument applies when the 'Verbose' value
is greater than 0. NumPrint mini-batches are
processed for each line of the convergence summary that is displayed
on the command line.
Example: 'NumPrint',5
Data Types: double | single
Number of tuning iterations for the 'sgd' solver,
specified as the comma-separated pair consisting of 'NumTuningIterations' and
a positive integer. This option is valid only for 'InitialLearningRate','auto'.
Example: 'NumTuningIterations',15
Data Types: double | single
Number of observations to use for tuning the initial learning
rate, specified as the comma-separated pair consisting of 'TuningSubsetSize' and
a positive integer value from 1 to n. This option
is valid only for 'InitialLearningRate','auto'.
Example: 'TuningSubsetSize',25
Data Types: double | single
SGD or LBFGS Options
Maximum number of iterations, specified as the comma-separated
pair consisting of 'IterationLimit' and a positive
integer. The default is 10000 for SGD and 1000 for LBFGS and mini-batch
LBFGS.
Each pass through a batch is an iteration. Each pass through all of the data is an epoch. If the data is divided into k mini-batches, then every epoch is equivalent to k iterations.
Example: 'IterationLimit',250
Data Types: double | single
Convergence tolerance on the step size, specified as the comma-separated
pair consisting of 'StepTolerance' and a positive
real scalar. The 'lbfgs' solver uses an absolute
step tolerance, and the 'sgd' solver uses a relative
step tolerance.
Example: 'StepTolerance',0.000005
Data Types: double | single
Mini-batch LBFGS Options
Maximum number of iterations per mini-batch LBFGS step, specified
as the comma-separated pair consisting of 'MiniBatchLBFGSIterations' and
a positive integer.
Example: 'MiniBatchLBFGSIterations',15
Data Types: double | single
Note
The mini-batch LBFGS algorithm is a combination of SGD and LBFGS methods. Therefore, all of the name-value pair arguments that apply to SGD and LBFGS solvers also apply to the mini-batch LBFGS algorithm.
Output Arguments
Neighborhood component analysis model for regression, returned
as a FeatureSelectionNCARegression object.
References
[1] Rasmussen, C. E., R. M. Neal, G. E. Hinton, D. van Camp, M. Revow, Z. Ghahramani, R. Kustra, and R. Tibshirani. The DELVE Manual, 1996, https://mlg.eng.cam.ac.uk/pub/pdf/RasNeaHinetal96.pdf.
[2] University of Toronto, Computer Science Department. Delve Datasets. http://www.cs.toronto.edu/~delve/data/datasets.html.
[3] Nash, W.J., T. L. Sellers, S. R. Talbot, A. J. Cawthorn, and W. B. Ford. "The Population Biology of Abalone (Haliotis species) in Tasmania. I. Blacklip Abalone (H. rubra) from the North Coast and Islands of Bass Strait." Sea Fisheries Division, Technical Report No. 48, 1994.
[4] Waugh, S. "Extending and Benchmarking Cascade-Correlation: Extensions to the Cascade-Correlation Architecture and Benchmarking of Feed-forward Supervised Artificial Neural Networks." University of Tasmania Department of Computer Science thesis, 1995.
[5] Lichman, M. UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science, 2013. http://archive.ics.uci.edu/ml.
Version History
Introduced in R2016b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)