opticalFlowFarneback
Object for estimating optical flow using Farneback method
Description
Create an optical flow object for estimating the direction and speed of moving
objects using the Farneback method. Use the object function estimateFlow to estimate the optical flow vectors. Using the reset object function, you can reset the internal state of the optical
flow object.
Creation
Description
opticFlow = opticalFlowFarneback
opticFlow = opticalFlowFarneback(Name,Value)Name,Value pair arguments. Any unspecified properties
have default values. Enclose each property name in quotes.
For example,
opticalFlowFarneback('NumPyramidLevels',3)
Properties
Object Functions
estimateFlow | Estimate optical flow |
reset | Reset the internal state of the optical flow estimation object |
Examples
Algorithms
The Farneback algorithm generates an image pyramid, where each level has a lower resolution compared to the previous level. When you select a pyramid level greater than 1, the algorithm can track the points at multiple levels of resolution, starting at the lowest level. Increasing the number of pyramid levels enables the algorithm to handle larger displacements of points between frames. However, the number of computations also increases. The diagram shows an image pyramid with three levels.
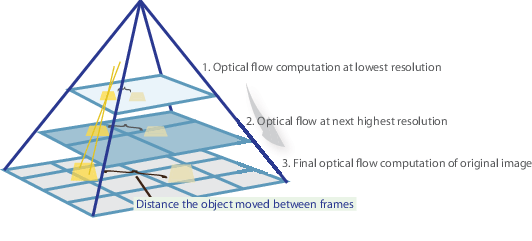
The tracking begins in the lowest resolution level, and continues until convergence. The point locations detected at a level are propagated as keypoints for the succeeding level. In this way, the algorithm refines the tracking with each level. The pyramid decomposition enables the algorithm to handle large pixel motions, which can be distances greater than the neighborhood size.
References
[1] Farneback, G. “Two-Frame Motion Estimation Based on Polynomial Expansion.” In Proceedings of the 13th Scandinavian Conference on Image Analysis, 363 - 370. Halmstad, Sweden: SCIA, 2003.
Extended Capabilities
Version History
Introduced in R2015b

