Semantic Segmentation of Multispectral Images Using Deep Learning
This example shows how to perform semantic segmentation of a multispectral image with seven channels using U-Net.
Semantic segmentation involves labeling each pixel in an image with a class. One application of semantic segmentation is tracking deforestation, which is the change in forest cover over time. Environmental agencies track deforestation to assess and quantify the environmental and ecological health of a region.
Deep learning based semantic segmentation can yield a precise measurement of vegetation cover from high-resolution aerial photographs. To increase classification accuracy, some data sets contain multispectral images that provide additional information about each pixel. For example, the Hamlin Beach State Park data set supplements the color images with three near-infrared channels that provide a clearer separation of the classes.
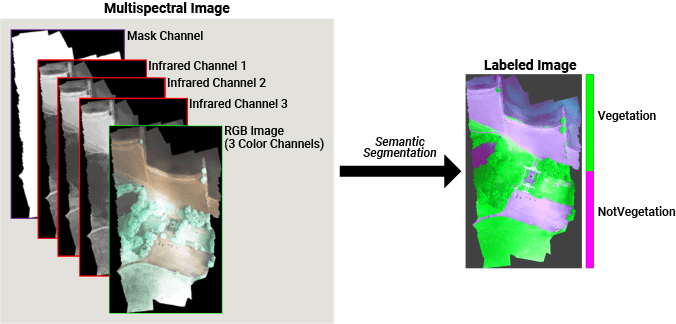
This example first shows you how to perform semantic segmentation using a pretrained U-Net and then use the segmentation results to calculate the extent of vegetation cover. Then, you can optionally train a U-Net network on the Hamlin Beach State Park data set using a patch-based training methodology.
Download Pretrained U-Net
Specify dataDir as the desired location of the trained network and data set.
dataDir = fullfile(tempdir,"rit18_data");Download a pretrained U-Net network.
trainedNet_url = "https://ssd.mathworks.com/supportfiles/"+ ... "vision/data/trainedMultispectralUnetModel_v2.zip"; downloadTrainedNetwork(trainedNet_url,dataDir); load(fullfile(dataDir,"trainedMultispectralUnetModel", ... "trainedMultispectralUnetModel_v2.mat"));
Download Data Set
This example uses a high-resolution multispectral data set to train the network [1]. The image set was captured using a drone over the Hamlin Beach State Park, NY. The data contains labeled training, validation, and test sets, with 18 object class labels. The size of the data file is 3.0 GB.
Download the MAT file version of the data set using the downloadHamlinBeachMSIData helper function. This function is attached to the example as a supporting file.
downloadHamlinBeachMSIData(dataDir);
Load the data set.
load(fullfile(dataDir,"rit18_data.mat")); whos train_data val_data test_data
Name Size Bytes Class Attributes test_data 7x12446x7654 1333663576 uint16 train_data 7x9393x5642 741934284 uint16 val_data 7x8833x6918 855493716 uint16
The multispectral image data is arranged as numChannels-by-width-by-height arrays. However, in MATLAB®, multichannel images are arranged as width-by-height-by-numChannels arrays. To reshape the data so that the channels are in the third dimension, use the permute function.
train_data = permute(train_data,[2 3 1]); val_data = permute(val_data,[2 3 1]); test_data = permute(test_data,[2 3 1]);
Confirm that the data has the correct structure.
whos train_data val_data test_data
Name Size Bytes Class Attributes test_data 12446x7654x7 1333663576 uint16 train_data 9393x5642x7 741934284 uint16 val_data 8833x6918x7 855493716 uint16
Visualize Multispectral Data
Display the center of each spectral band in nanometers.
disp(band_centers)
490 550 680 720 800 900
In this data set, the RGB color channels are the 3rd, 2nd, and 1st image channels, respectively. Display the RGB component of the training, validation, and test images as a montage. To make the images appear brighter on the screen, equalize their histograms by using the histeq function.
rgbTrain = histeq(train_data(:,:,[3 2 1]));
rgbVal = histeq(val_data(:,:,[3 2 1]));
rgbTest = histeq(test_data(:,:,[3 2 1]));
montage({rgbTrain,rgbVal,rgbTest},BorderSize=10,BackgroundColor="white")
title("RGB Component of Training, Validation, and Test Image (Left to Right)")
The 4th, 5th, and 6th channels of the data correspond to near-infrared bands. Equalize the histogram of these three channels for the training image, then display these channels as a montage. The channels highlight different components of the image based on their heat signatures. For example, the trees are darker in the 4th channel than in the other two infrared channels.
ir4Train = histeq(train_data(:,:,4));
ir5Train = histeq(train_data(:,:,5));
ir6Train = histeq(train_data(:,:,6));
montage({ir4Train,ir5Train,ir6Train},BorderSize=10,BackgroundColor="white")
title("Infrared Channels 4, 5, and 6 (Left to Right) of Training Image ")
The 7th channel of the data is a binary mask that indicates the valid segmentation region. Display the mask for the training, validation, and test images.
maskTrain = train_data(:,:,7);
maskVal = val_data(:,:,7);
maskTest = test_data(:,:,7);
montage({maskTrain,maskVal,maskTest},BorderSize=10,BackgroundColor="white")
title("Mask of Training, Validation, and Test Image (Left to Right)")
Visualize Ground Truth Labels
The labeled images contain the ground truth data for the segmentation, with each pixel assigned to one of the 18 classes. Get a list of the classes with their corresponding IDs.
disp(classes)
0. Other Class/Image Border 1. Road Markings 2. Tree 3. Building 4. Vehicle (Car, Truck, or Bus) 5. Person 6. Lifeguard Chair 7. Picnic Table 8. Black Wood Panel 9. White Wood Panel 10. Orange Landing Pad 11. Water Buoy 12. Rocks 13. Other Vegetation 14. Grass 15. Sand 16. Water (Lake) 17. Water (Pond) 18. Asphalt (Parking Lot/Walkway)
This example aims to segment the images into two classes: vegetation and non-vegetation. Define the target class names.
classNames = ["NotVegetation" "Vegetation"];
Group the 18 original classes into the two target classes for the training and validation data. "Vegetation" is a combination of the original classes "Tree", "Other Vegetation", and "Grass", which have class IDs 2, 13, and 14. The original class "Other Class/Image Border" with class ID 0 belongs to the background class. All other original classes belong to the target label "NotVegetation".
vegetationClassIDs = [2 13 14]; nonvegetationClassIDs = setdiff(1:length(classes),vegetationClassIDs); labelsTrain = zeros(size(train_labels),"uint8"); labelsTrain(ismember(train_labels,nonvegetationClassIDs)) = 1; labelsTrain(ismember(train_labels,vegetationClassIDs)) = 2; labelsVal = zeros(size(val_labels),"uint8"); labelsVal(ismember(val_labels,nonvegetationClassIDs)) = 1; labelsVal(ismember(val_labels,vegetationClassIDs)) = 2;
Save the ground truth validation labels as a PNG file. The example uses this file to calculate accuracy metrics.
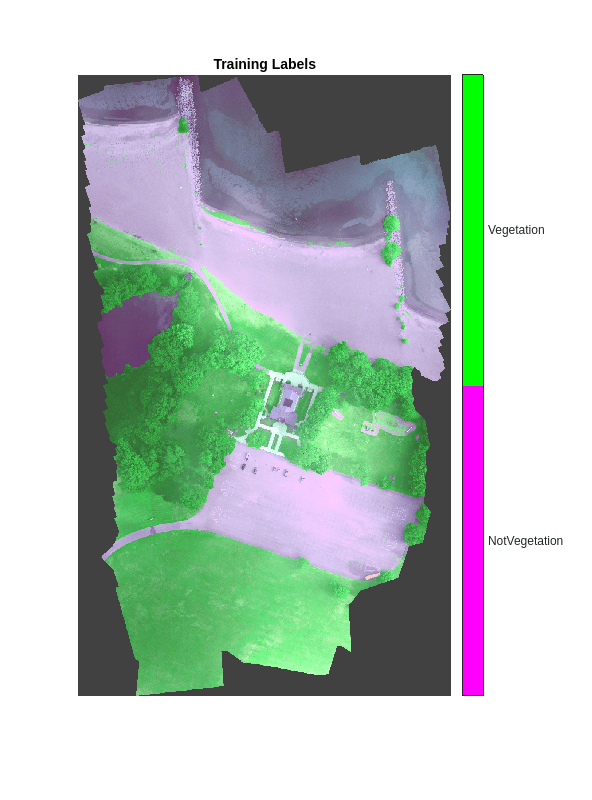
imwrite(labelsVal,"gtruth.png");Overlay the labels on the histogram-equalized RGB training image. Add a color bar to the image.
cmap = [1 0 1;0 1 0]; B = labeloverlay(rgbTrain,labelsTrain,Transparency=0.8,Colormap=cmap); imshow(B,cmap) title("Training Labels") numClasses = numel(classNames); ticks = 1/(numClasses*2):1/numClasses:1; colorbar(TickLabels=cellstr(classNames), ... Ticks=ticks,TickLength=0,TickLabelInterpreter="none");
Perform Semantic Segmentation on Test Image
The size of the image prevents segmenting the entire image at once. Instead, segment the image using a blocked image approach. This approach can scale to very large files because it loads and processes one block of data at a time.
Create a blocked image containing the six spectral channels of the test data by using the blockedImage function.
patchSize = [1024 1024]; bimTest = blockedImage(test_data(:,:,1:6),BlockSize=patchSize);
Segment a block of data by using the semanticseg function. Call the sematicseg function on all blocks in the blocked image by using the apply function.
bimSeg = apply(bimTest,@(bs)semanticseg(bs.Data,net,Outputtype="uint8"), ... PadPartialBlocks=true,PadMethod=0);
Assemble all of the segmented blocks into a single image into the workspace by using the gather function.
segmentedImage = gather(bimSeg);
To extract only the valid portion of the segmentation, multiply the segmented image by the mask channel of the test data.
segmentedImage = segmentedImage .* uint8(maskTest~=0);
imshow(segmentedImage,[])
title("Segmented Image")
The output of semantic segmentation is noisy. Perform post image processing to remove noise and stray pixels. Remove salt-and-pepper noise from the segmentation by using the medfilt2 function. Display the segmented image with the noise removed.
segmentedImage = medfilt2(segmentedImage,[7 7]);
imshow(segmentedImage,[]);
title("Segmented Image with Noise Removed")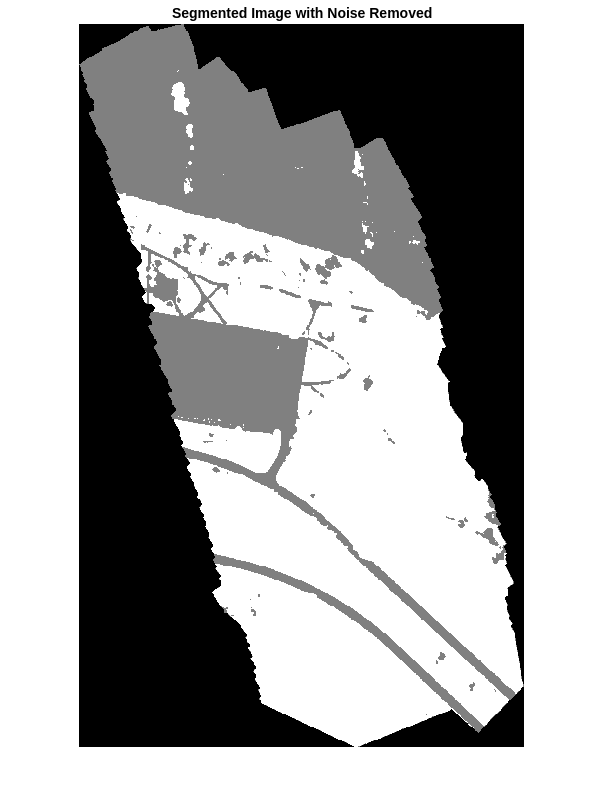
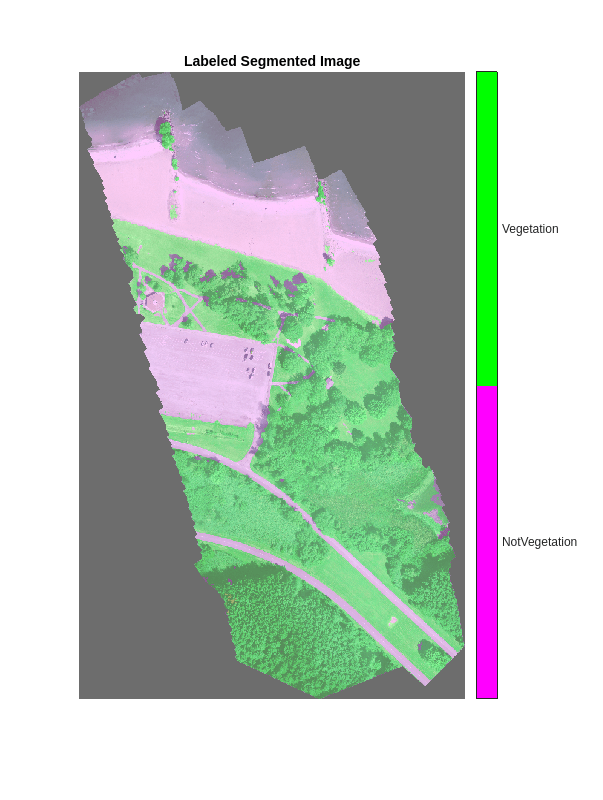
Overlay the segmented image on the histogram-equalized RGB validation image.
B = labeloverlay(rgbTest,segmentedImage,Transparency=0.8,Colormap=cmap); imshow(B,cmap) title("Labeled Segmented Image") colorbar(TickLabels=cellstr(classNames), ... Ticks=ticks,TickLength=0,TickLabelInterpreter="none");
Calculate Extent of Vegetation Cover
The semantic segmentation results can be used to answer pertinent ecological questions. For example, what percentage of land area is covered by vegetation? To answer this question, find the number of pixels labeled vegetation in the segmented test image. Also, find the total number of pixels in the ROI by counting the number of nonzero pixels in the segmented image.
vegetationPixels = ismember(segmentedImage(:),vegetationClassIDs); numVegetationPixels = sum(vegetationPixels(:)); numROIPixels = nnz(segmentedImage);
Calculate the percentage of vegetation cover by dividing the number of vegetation pixels by the number of pixels in the ROI.
percentVegetationCover = (numVegetationPixels/numROIPixels)*100; disp("The percentage of vegetation cover is "+percentVegetationCover+"%");
The percentage of vegetation cover is 60.7028%
The rest of the example shows how to train U-Net on the Hamlin Beach data set.
Create Blocked Image Datastores for Training
Use a blocked image datastore to feed the training data to the network. This datastore extracts multiple corresponding patches from an image datastore and pixel label datastore that contain ground truth images and pixel label data.
Read the training images, training labels, and mask as blocked images.
inputTileSize = [256 256]; bim = blockedImage(train_data(:,:,1:6),BlockSize=inputTileSize); bLabels = blockedImage(labelsTrain,BlockSize=inputTileSize); bmask = blockedImage(maskTrain,BlockSize=inputTileSize);
Select blocks of image data that overlap with the mask.
overlapPct = 0.185; blockOffsets = round(inputTileSize.*overlapPct); bls = selectBlockLocations(bLabels, ... BlockSize=inputTileSize,BlockOffsets=blockOffsets, ... Masks=bmask,InclusionThreshold=0.95);
One-hot encode the labels.
labelsTrain1hot = onehotencode(labelsTrain,3,ClassNames=1:2); labelsTrain1hot(isnan(labelsTrain1hot)) = 0; bLabels = blockedImage(labelsTrain1hot,BlockSize=inputTileSize);
Write the data to blocked image datastores by using the blockedImageDatastore function.
bimds = blockedImageDatastore(bim,BlockLocationSet=bls,PadMethod=0); bimdsLabels = blockedImageDatastore(bLabels,BlockLocationSet=bls,PadMethod=0);
Create a CombinedDatastore from the two blocked image datastores.
dsTrain = combine(bimds,bimdsLabels);
The blocked image datastore dsTrain provides mini-batches of data to the network at each iteration of the epoch. Preview the datastore to explore the data.
preview(dsTrain)
ans=1×2 cell array
{256×256×6 uint16} {256×256×2 double}
Create U-Net Network
This example uses a variation of the U-Net network. In U-Net, the initial series of convolutional layers are interspersed with max pooling layers, successively decreasing the resolution of the input image. These layers are followed by a series of convolutional layers interspersed with upsampling operators, successively increasing the resolution of the input image [2]. The name U-Net comes from the fact that the network can be drawn with a symmetric shape like the letter U.
Specify hyperparameters of the U-Net. The input depth is the number of hyperspectral channels, 6.
inputDepth = 6;
Create the U-Net network using the unet function.
unetNetwork = unet([inputTileSize inputDepth],numClasses);
Define Loss Function
Define a custom loss function called lossFcn that calculates cross entropy loss over all unmasked pixels of an image.
function loss = lossFcn(Y,T) mask = ~isnan(T); T(isnan(T)) = 0; loss = crossentropy(Y,T,Mask=mask); end
Select Training Options
Train the network using stochastic gradient descent with momentum (SGDM) optimization. Specify the hyperparameter settings for SGDM by using the trainingOptions (Deep Learning Toolbox) function. To enable gradient clipping, specify the GradientThreshold name-value argument as 0.05 and specify the GradientThresholdMethod to use the L2-norm of the gradients.
maxEpochs = 70; minibatchSize = 16; options = trainingOptions("sgdm", ... InitialLearnRate=0.05, ... MaxEpochs=maxEpochs, ... MiniBatchSize=minibatchSize, ... L2Regularization=0.001, ... LearnRateDropPeriod=10, ... LearnRateSchedule="piecewise", ... GradientThreshold=0.05, ... Shuffle="every-epoch", ... VerboseFrequency=200);
Train the Network
To train the network, set the doTraining variable in the following code to true. Train the model by using the trainnet (Deep Learning Toolbox) function. Specify the loss as the custom loss function, lossFcn. By default, the trainnet function uses a GPU if one is available. Training on a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the trainnet function uses the CPU. To specify the execution environment, use the ExecutionEnvironment training option.
doTraining =false; if doTraining net = trainnet(dsTrain,unetNetwork,@lossFcn,options); modelDateTime = string(datetime("now",Format="yyyy-MM-dd-HH-mm-ss")); save(fullfile(dataDir,"multispectralUnet-"+modelDateTime+".mat"),"net"); end
Evaluate Segmentation Accuracy
Segment the validation data.
Create a blocked image containing the six spectral channels of the validation data by using the blockedImage function.
bimVal = blockedImage(val_data(:,:,1:6),BlockSize=patchSize);
Segment a block of data by using the semanticseg function. Call the sematicseg function on all blocks in the blocked image by using the apply function.
bimSeg = apply(bimVal,@(bs)semanticseg(bs.Data,net,Outputtype="uint8"),... PadPartialBlocks=true,PadMethod=0);
Assemble all of the segmented blocks into a single image into the workspace by using the gather function.
segmentedImage = gather(bimSeg);
Save the segmented image as a PNG file.
imwrite(segmentedImage,"results.png");Load the segmentation results and ground truth labels by using the pixelLabelDatastore function.
pixelLabelIDs = [1 2]; pxdsResults = pixelLabelDatastore("results.png",classNames,pixelLabelIDs); pxdsTruth = pixelLabelDatastore("gtruth.png",classNames,pixelLabelIDs);
Measure the accuracy of the semantic segmentation by using the evaluateSemanticSegmentation function. The global accuracy score indicates that over 96% of the pixels are classified correctly.
ssm = evaluateSemanticSegmentation(pxdsResults,pxdsTruth);
Evaluating semantic segmentation results
----------------------------------------
* Selected metrics: global accuracy, class accuracy, IoU, weighted IoU, BF score.
* Processed 1 images.
* Finalizing... Done.
* Data set metrics:
GlobalAccuracy MeanAccuracy MeanIoU WeightedIoU MeanBFScore
______________ ____________ _______ ___________ ___________
0.9694 0.9704 0.9406 0.94064 0.79474
References
[1] Kemker, R., C. Salvaggio, and C. Kanan. "High-Resolution Multispectral Dataset for Semantic Segmentation." CoRR, abs/1703.01918. 2017.
[2] Ronneberger, O., P. Fischer, and T. Brox. "U-Net: Convolutional Networks for Biomedical Image Segmentation." CoRR, abs/1505.04597. 2015.
[3] Kemker, Ronald, Carl Salvaggio, and Christopher Kanan. "Algorithms for Semantic Segmentation of Multispectral Remote Sensing Imagery Using Deep Learning." ISPRS Journal of Photogrammetry and Remote Sensing, Deep Learning RS Data, 145 (November 1, 2018): 60-77. https://doi.org/10.1016/j.isprsjprs.2018.04.014.
See Also
blockedImage | apply | selectBlockLocations | blockedImageDatastore | semanticseg | evaluateSemanticSegmentation | unet | dlnetwork (Deep Learning Toolbox) | trainingOptions (Deep Learning Toolbox) | trainnet (Deep Learning Toolbox)
Topics
- Get Started with Semantic Segmentation Using Deep Learning
- Semantic Segmentation Using Deep Learning
- Label Large Images in the Image Labeler
- Datastores for Deep Learning (Deep Learning Toolbox)