Latest Contributions
The Cody Contest 2025 has officially wrapped up! Over the past 4 weeks, more than 700 players submitted over 20,000 solutions. In addition, participants shared 20+ high-quality Tips & Tricksarticles—resources that will benefit Cody users for years to come.
Now it’s time to announce the winners.
🎉 Week 4 winners:
Weekly Prizes for Contest Problem Group Finishers:
@JKMSMKJ, @Yu Zhang, @Oliver Jaros, @Pauli Huusari, @Karl, @Marcos Silveira, @goc3, @Ildeberto de los Santos Ruiz, @Norberto, @Eric
Weekly Prizes for Contest Problem Group Solvers:
Weekly Prizes for Tips & Tricks Articles:
This week’s prize goes to @WANG Zi-Xiang. See the comments from our judge and problem group author @Matt Tearle:
‘We had a lot of great tips for solving Cody problems in general and the contest problems specifically. But we all know there are those among us who, having solved the problem, still want to tinker and make their code better. There are different definitions of "better", but code size remains the base metric in Cody. Enter Wang Zi-Xiang who compiled a list of many tips for reducing Cody size. This post also generated some great discussion (even prompting our insane autocrat, Lord Ned himself, to chime in). I particularly like the way that, while reducing Cody size often requires some arcane tricks that would normally be considered bad coding practice, the intellectual activity of trying to "game the system" makes you consider different programming approaches, and sometimes leads you to learn corners of MATLAB that you didn't know.’
🏆 Grand Prizes for the Main Round
Team Relentless Coders:
2nd Place: @Roberto
Team Creative Coders:
Team Cool Coders
Congratulations to all! Securing a top position on the leaderboard requires not only advanced MATLAB skills but also determination and consistency throughout the four-week contest. You will receive Amazon gift cards.
🥇 Winning Team
The competition was incredibly tight—we even had to use the tie-breaker rule.
Both Team Cool Coders and Team Relentless Coders achieved 16 contest group finishers. However, the last finisher on Cool Coders completed the problem group at 1:02 PM on Dec 7, while the last finisher on Relentless Coders finished at 9:47 PM the same day.
Such a close finish! Congratulations to Team Cool Coders, who have earned the Winning Team Finishers badge.

🎬 Bonus Round
Invitations have been sent to the 6 players who qualified for the Bonus Round. Stay tuned for updates—including the Big Watch Party afterward!
Congratulations again to all winners! We’ll be reaching out after the contest ends. It has been an exciting, rewarding, and knowledge-packed journey.
See you next year!
Over the past three weeks, players have been having great fun solving problems, sharing knowledge, and connecting with each other. Did you know over 15,000 solutions have already been submitted?
This is the final week to solve Cody problems and climb the leaderboard in the main round. Remember: solving just one problem in the contest problem group gives you a chance to win MathWorks T-shirts or socks.
🎉 Week 3 Winners:
Weekly Prizes for Contest Problem Group Finishers:
@Umar, @David Hill, @Takumi, @Nicolas, @WANG Zi-Xiang, @Rajvir Singh Gangar, @Roberto, @Boldizsar, @Abi, @Antonio
Weekly Prizes for Contest Problem Group Solvers:
Weekly Prizes for Tips & Tricks Articles:
This week’s prize goes to @Cephas. See the comments from our judge and problem group author @Matt Tearle:
'Some folks have posted deep dives into how to tackle specific problems in the contest set. But others have shared multiple smaller, generally useful tips. This week, I want to congratulate the cumulative contribution of Cool Coder Cephas, who has shared several of my favorite MATLAB techniques, including logical indexing, preallocation, modular arithmetic, and more. Cephas has also given some tips applying these MATLAB techniques to specific contest problems, such as using a convenient MATLAB function to vectorize the Leaderboard problem. Tip for Problem 61059 – Leaderboard for the Nedball World Cup:'
Congratulations to all Week 3 winners! Let’s carry this momentum into the final week!
In just two weeks, the competition has become both intense and friendly as participants race to climb the team leaderboard, especially in Team Creative, where @Mehdi Dehghan currently leads with 1400+ points, followed by @Vasilis Bellos with 900+ points.
There’s still plenty of time to participate before the contest's main round ends on December 7. Solving just one problem in the contest problem group gives you a chance to win MathWorks T-shirts or socks. Completing the entire problem group not only boosts your odds but also helps your team win.
🎉 Week 2 Winners:
Weekly Prizes for Contest Problem Group Finishers:
@Cephas, @Athi, @Bin Jiang, @Armando Longobardi, @Simone, @Maxi, @Pietro, @Hong Son, @Salvatore, @KARUPPASAMYPANDIYAN M
Weekly Prizes for Contest Problem Group Solvers:
Weekly Prizes for Tips & Tricks Articles:
This week’s prize goes to @Athi for the highly detailed post Solving Systematically The Clueless - Lord Ned in the Game Room.
Comment from the judge:
Shortly after the problem set dropped, several folks recognized that the final problem, "Clueless", was a step above the rest in difficulty. So, not surprisingly, there were a few posts in the discussion boards related to how to tackle this problem. Athi, of the Cool Coders, really dug deep into how the rules and strategies could be turned into an algorithm. There's always more than one way to tackle any difficult programming problem, so it was nice to see some discussion in the comments on different ways you can structure the array that represents your knowledge of who has which cards.
Congratulations to all Week 2 winners! Let’s keep the momentum going!
In just one week, we have hit an amazing milestone: 500+ players registered and 5000+ solutions submitted! We’ve also seen fantastic Tips & Tricks articles rolling in, making this contest a true community learning experience.
And here’s the best part: you don’t need to be a top-ranked player to win. To encourage more casual and first-time players to jump in, we’re introducing new weekly prizes starting Week 2!
New Casual Player Prizes:
- 5 extra MathWorks T-shirts or socks will be awarded every week.
- All you need to qualify is to register and solve one problem in the Contest Problem Group.
Jump in, try a few problems, and don’t be shy to ask questions in your team’s channel. You might walk away with a prize!
Week 1 Winners:
Weekly Prizes for Contest Problem Group Finishers:
@Mazhar, @Julien, @Mohammad Aryayi, @Pawel, @Mehdi Dehghan, @Christian Schröder, @Yolanda, @Dev Gupta, @Tomoaki Takagi, @Stefan Abendroth
Weekly Prizes for Tips & Tricks Articles:
We had a lot of people share useful tips (including some personal favorite MATLAB tricks). But Vasilis Bellos went *deep* into the Bridges of Nedsburg problem. Fittingly for a Creative Coder, his post was innovative and entertaining, while also cleverly sneaking in some hints on a neat solution method that wasn't advertised in the problem description.
Congratulations to all Week 1 winners! Prizes will be awarded after the contest ends. Let’s keep the momentum going!
What a fantastic start to Cody Contest 2025! In just 2 days, over 300 players joined the fun, and we already have our first contest group finishers. A big shoutout to the first finisher from each team:
- Team Creative Coders: @Mehdi Dehghan
- Team Cool Coders: @Pawel
- Team Relentless Coders: @David Hill
- 🏆 First finisher overall: Mehdi Dehghan
Other group finishers: @Bin Jiang (Relentless), @Mazhar (Creative), @Vasilis Bellos (Creative), @Stefan Abendroth (Creative), @Armando Longobardi (Cool), @Cephas (Cool)
Kudos to all group finishers! 🎉
Reminder to finishers: The goal of Cody Contest is learning together. Share hints (not full solutions) to help your teammates complete the problem group. The winning team will be the one with the most group finishers — teamwork matters!
To all players: Don’t be shy about asking for help! When you do, show your work — include your code, error messages, and any details needed for others to reproduce your results.
Keep solving, keep sharing, and most importantly — have fun!
The main round of Cody Contest 2025 kicks off today! Whether you’re a beginner or a seasoned solver, now’s your time to shine.
Here’s how to join the fun:
- Pick your team — choose one that matches your coding personality.
- Solve Cody problems — gain points and climb the leaderboard.
- Finish the Contest Problem Group — help your team win and unlock chances for weekly prizes by finishing the Cody Contest 2025 problem group.
- Share Tips & Tricks — post your insights to win a coveted MathWorks Yeti Bottle.
- Bonus Round — 2 players from each team will be invited to a fun live code-along event!
- Watch Party – join the big watch event to see how top players tackle Cody problems
Contest Timeline:
- Main Round: Nov 10 – Dec 7, 2025
- Bonus Round: Dec 8 – Dec 19, 2025
Big prizes await — MathWorks swag, Amazon gift cards, and shiny virtual badges!
We look forward to seeing you in the contest — learn, compete, and have fun!
We are thrilled to announce the grand prize winners of our MATLAB Shorts Mini Hack contest! This year, we invited the MATLAB Graphics and Charting team, the authors of the MATLAB functions used in every entry, to be our judges. After careful consideration, they have selected the top three winners:
Judge comments: Realism & detailed comments; wowed us with Manta Ray
2nd place – Jenny Bosten
Judge comments: Topical hacks : Auroras & Wind turbine; beautiful landscapes & nightscapes
3rd place - Vasilis Bellos
Judge comments: Nice algorithms & extra comments; can’t go wrong with Pumpkins
Judge comments: Impressive spring & cubes!
In addition, after validating the votes, we are pleased to announce the top 10 participants on the leaderboard:
Congratulations to all! Your creativity and skills have inspired many of us to explore and learn new skills, and make this contest a big success!
Over the past 4 weeks, 250+ creative short movies have been crafted. We had a lot of fun and, more importantly, learned new skills from each other! Now it’s time to announce week 4 winners.
Nature:
3D:
Seamless loop:
Holiday:
Fractal:
Congratulations! Each of you won your choice of a T-shirt, a hat, or a coffee mug. We will contact you after the contest ends.
Weekly Special Prizes
Thank you for sharing your tips & tricks with the community. These great technical articles will benefit community users for many years. You won a limited-edition pair of MATLAB Shorts!

In week 5, let’s take a moment to sit back, explore all of the interesting entries, and cast your votes. Reflect what you have learned or which entries you like most. Share anything in our Discussions area! There is still time to win our limited-edition MATLAB Shorts.
Dear MATLAB contest enthusiasts,
Welcome to the third installment of our interview series with top contest participants! This time we had the pleasure of talking to our all-time rock star – @Jenny Bosten. Every one of her entries is a masterpiece, demonstrating a deep understanding of the relationship between mathematics and aesthetics. Even Cleve Moler, the original author of MATLAB, is impressed and wrote in his blog: "Her code for Time Lapse of Lake View to the West shows she is also a wizard of coordinate systems and color maps."
you to read it to learn more about Jenny’s journey, her creative process, and her favorite entries.
Question: Who would you like to see featured in our next interview? Let us know your thoughts in the comments!
There are so many incredible entries created in week 1. Now, it’s time to announce the weekly winners in various categories!
Nature & Space:
Seamless Loop:
Abstract:
Remix of previous Mini Hack entries:
Early Discovery
Holiday:
Congratulations to all winners! Each of you won your choice of a T-shirt, a hat, or a coffee mug. We will contact you after the contest ends.
In week 2, we’d love to see and award more entries in the ‘Seamless Loop’ category. We can't wait to see your creativity shine!
Tips for Week 2:
1.Use AI for assistance
The code from the Mini Hack entries can be challenging, even for experienced MATLAB users. Utilize AI tools for MATLAB to help you understand the code and modify the code. Here is an example of a remix assisted by AI. @Hans Scharler used MATLAB GPT to get an explanation of the code and then prompted it to ‘change the background to a starry night with the moon.’
2. Share your thoughts
Share your tips & tricks, experience of using AI, or learnings with the community. Post your knowledge in the Discussions' general channel (be sure to add the tag 'contest2024') to earn opportunities to win the coveted MATLAB Shorts.
3. Ensure Thumbnails Are Displayed:
You might have noticed that some entries on the leaderboard lack a thumbnail image. To fix this, ensure you include ‘drawframe(1)’ in your code.
We are thrilled to see the incredible short movies created during Week 3. The bar has been set exceptionally high! This week, we invited our Community Advisory Board (CAB) members to select winners. Here are their picks:
Mini Hack Winners - Week 3
Game:
Holidays:
Fractals:
Realism:
Great Remixes:
Seamless loop:
Fun:
Weekly Special Prizes
Thank you for sharing your tips & tricks with the community. You won a limited-edition MATLAB Shorts.

We still have plenty of MATLAB Shorts available, so be sure to create your posts before the contest ends. Don't miss out on the opportunity to showcase your creativity!
Just in two weeks, we already have 150+ entries! We are so impressed by your creative styles, artistic talents, and ingenious programming techniques.
Now, it’s time to announce the weekly winners!
Mini Hack Winners - Week 2
Seamless loop:
Nature & Animals:
Game:
Synchrony:
Remix of previous Mini Hack entries
Movie:
Congratulations to all winners! Each of you won your choice of a T-shirt, a hat, or a coffee mug. We will contact you after the contest ends.
In week 3, we’d love to see and award entries in the ‘holiday’ category.
Weekly Special Prizes
Thank you for sharing your tips & tricks with the community. You won limited-edition MATLAB Shorts.
We highly encourage everyone to share various types of content, such as tips and tricks for creating animations, background stories of your entry, or learnings you've gained from the contest.
We're excited to announce that the 2024 Community Contest—MATLAB Shorts Mini Hack starts today! The contest will run for 5 weeks, from Oct. 7th to Nov. 10th.
What creative short movies will you create? Let the party begin, and we look forward to seeing you all in the contest!
Over the past week, we have seen many creative and compelling short movies! Now, let the voting begin! Cast your votes for the short movies you love. Authors, share your creations with friends, classmates, and colleagues. Let's showcase the beauty of mathematics to the world!
We know that one of the key goals for joining the Mini Hack contest is to LEARN! To celebrate knowledge sharing, we have special prizes—limited-edition MATLAB Shorts—up for grabs!

These exclusive prizes can only be earned through the MATLAB Shorts Mini Hack contest. Interested? Share your knowledge in the Discussions' general channel (be sure to add the tag 'contest2024') to earn opportunities to win the coveted MATLAB Shorts. You can share various types of content, such as tips and tricks for creating animations, background stories of your entry, or learnings you've gained from the contest. We will select different types of winners each week.
We also have an exciting feature announcement: you can now experiment with code in MATLAB Online. Simply click the 'Open in MATLAB Online' button above the movie preview section. Even better! ‘Open in MATLAB Online’ is also available in previous Mini Hack contests!
We look forward to seeing more amazing short movies in Week 2!
Dear contest participants,
The 2024 Community Contest—MATLAB Shorts Mini Hack—is just one week away! Last year, we challenged you to create a 48-frame, 2-second animation. This year, we're doubling the fun by increasing the frame count to 96 and adding audio support. Your mission? Create a short movie!
As always, whether you are a seasoned MATLAB user or just a beginner, you can participate in the contest and have opportunities to win amazing prizes.

Timeframe:
- The contest will run for 5 weeks, from Oct. 7th to Nov. 10th, Eastern Time.
General Rules:
- The first week is dedicated to entry creation, and the fifth week is reserved for voting only.
- Create a 96-frame, 4-second animation and add audio. We will loop it 3 times to create a 12-second short movie for you.
- The character limit remains at 2,000 characters.
Prizes
- You will have opportunities to win compelling prizes, including Amazon gift cards, MathWorks T-shirts, and virtual badges. We will give out both weekly prizes and grand prizes.
Warm-up!
With one week left before the contest begins, we recommend you warm up by reading a fantastic article: Walkthrough: making Little Nemo's airship in MATLAB by @Tim. The article shares both technical insights and the challenges encountered along the way.
The MATLAB Central Community Team
We are thrilled to announce the grand prize winners of our MATLAB Flipbook contest! This year, we invited the MATLAB Graphics Infrastructure team, renowned for their expertise in exporting and animation workflows, to be our judges. After careful consideration, they have selected the top three winners:
Judge comments: Creative and realistic rendering with well-written code
2nd place - Christmas Tree / Zhaoxu Liu
Judge comments: Festive and advanced animation that is appropriate to the current holiday season.
Judge comments: Nice translation of existing shader logic to MATLAB that produces an advanced and appealing visual effect.
In addition, after validating the votes, we are pleased to announce the top 10 participants on the leaderboard:
- Tim
- Zhaoxu Liu / slandarer
- KARUPPASAMYPANDIYAN M
- Dhimas Mahardika S.Si., M.Mat
- Augusto Mazzei
- Jenny Bosten
- Lucas
- Jr
- Victoria
- ME
Congratulations to all! Your creativity and skills have inspired many of us to explore and learn new skills, and make this contest a big success!
Dear MATLAB contest enthusiasts,
In the 2023 MATLAB Mini Hack Contest, Tim Marston captivated everyone with his incredible animations, showcasing both creativity and skill, ultimately earning him the 1st prize.
We had the pleasure of interviewing Tim to delve into his inspiring story. You can read the full interview on MathWorks Blogs: Community Q&A – Tim Marston.
Last question: Are you ready for this year’s Mini Hack contest?
Dear MATLAB contest enthusiasts,
I believe many of you have been captivated by the innovative entries from Zhaoxu Liu / slanderer, in the 2023 MATLAB Flipbook Mini Hack contest.


Ever wondered about the person behind these creative entries? What drives a MATLAB user to such levels of skill? And what inspired his participation in the contest? We were just as curious as you are!
We were delighted to catch up with him and learn more about his use of MATLAB. The interview has recently been published in MathWorks Blogs. For an in-depth look into his insights and experiences, be sure to read our latest blog post: Community Q&A – Zhaoxu Liu.
But the conversation doesn't end here! Who would you like to see featured in our next interview? Drop their name in the comments section below and let us know who we should reach out to next!
Greetings to all MATLAB users,
Although the MATLAB Flipbook contest has concluded, the pursuit of ‘learning while having fun’ continues. I would like to take this opportunity to highlight some recent insightful technical articles from a standout contest participant – Zhaoxu Liu / slandarer.
Zhaoxu has contributed eight informative articles to both the Tips & Tricks and Fun channels in our new Discussions area. His articles offer practical advice on topics such as customizing legends, constructing chord charts, and adding color to axes. Additionally, he has shared engaging content, like using MATLAB to create an interactive dragon that follows your mouse cursor, a nod to the upcoming Year of the Dragon in 2024!
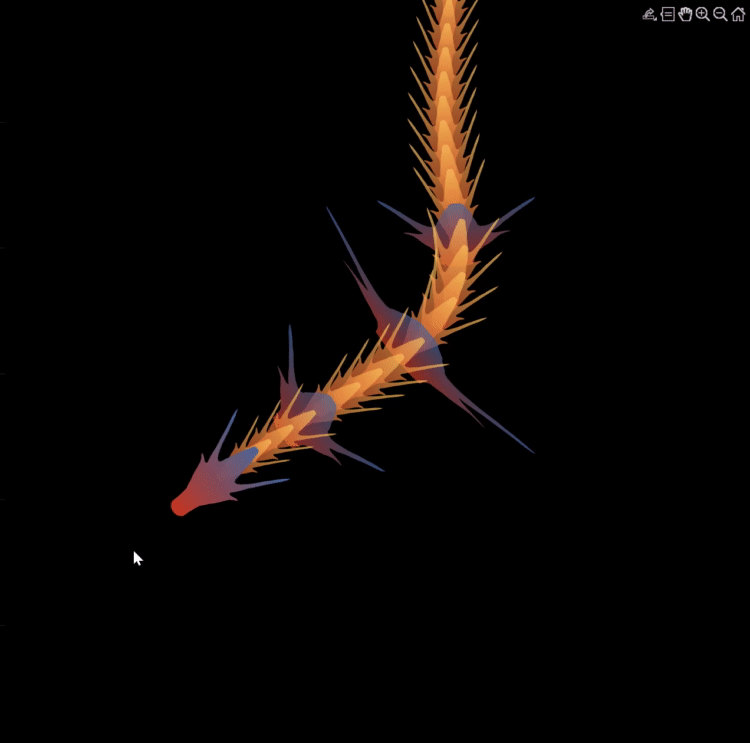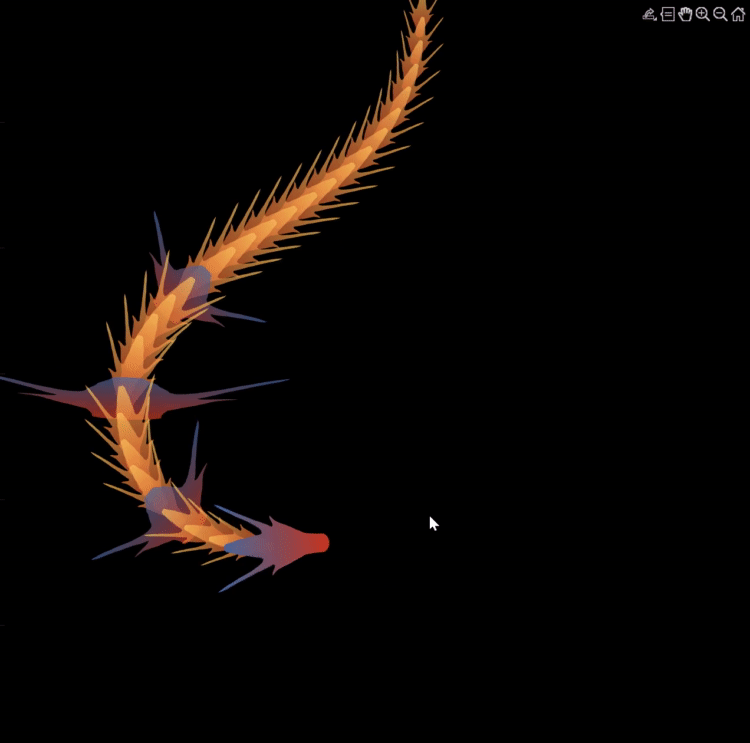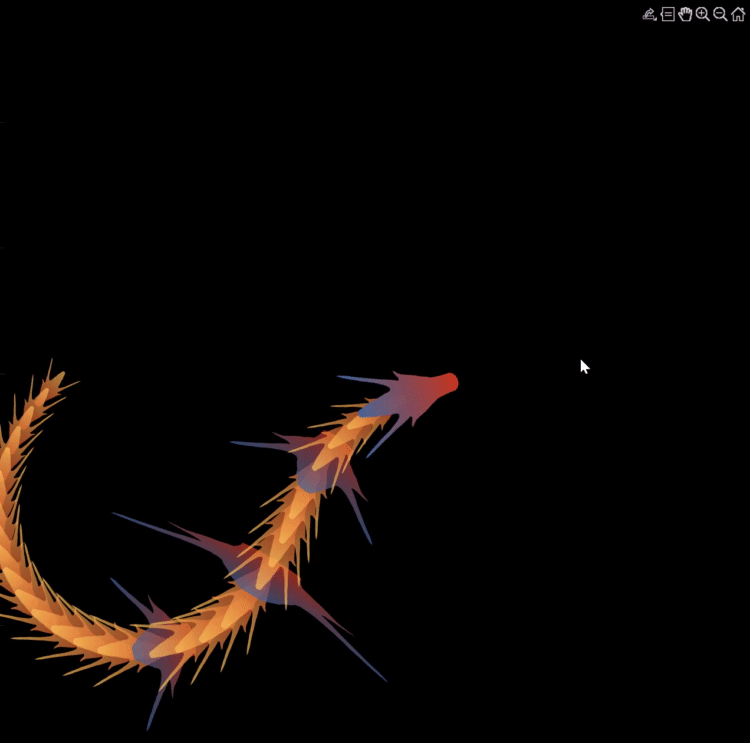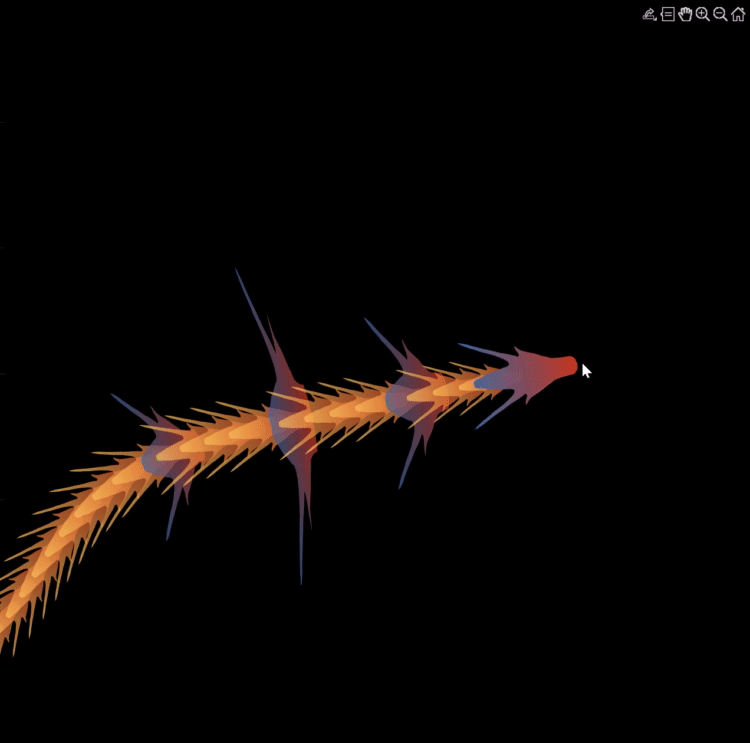
I invite you to explore these articles for both enjoyment and education, and I hope you'll find new techniques to incorporate into your work.
Our community is full of individuals skilled in MATLAB, and we're always eager to learn from one another. Who would you like to see featured next? Or perhaps you have some tips & tricks of your own to contribute. Remember, sharing knowledge is a collaborative effort, as Confucius wisely stated, 'When I walk along with two others, they may serve me as my teachers.'
Let's maintain our commitment to a continuous learning journey. This could be the perfect warm-up for the upcoming 2024 contest.
About Meta Contests
The MathWorks community has been enjoying programming contests since 1998!
Discuss, share your experiences, and celebrate your wins in the MATLAB Community contests.
Discuss, share your experiences, and celebrate your wins in the MATLAB Community contests.
Recent Contests
Oct 2024
MATLAB Shorts Mini Hack
Nov 2023MATLAB Flipbook Mini Hack
Oct 2022Cody 10th Year Anniversary
Oct 2022MATLAB Mini Hack
View AllFEATURED
A masterpiece. I admire the combination of mathematic understanding, implementation skills, and aesthetics.
Stefan Abendroth
