Over the weekend I came across a pi approximation using durations of years and weeks (image below, Wolfram, eq. 89), accurate to 6 digits using the average Gregorian year (365.2425 days).
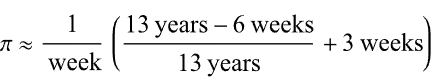
Here it is in MATLAB. I divided by 1 week at the end rather than multiplying by its reciprocal because you can’t divide a numeric by a duration in MATLAB (1/week).
weeks = @(n)n*days(7);
piApprox = ((years(13)-weeks(6))/years(13) + weeks(3)) / weeks(1)
% piApprox = 3.141593493469302
Here’s a breakdown
- The first argument becomes 12.885 yrs / 13 yrs or 0.99115
- Add three weeks: 0.99115 + 3 weeks = 21.991 days
- The reduced fraction becomes 21.991 days / 7 days
Now it looks a lot closer to the more familiar approximation for pi 22/7 but with greater precision!
2 Comments
Time Descending
Funny. A small part of me that is an engineer finds it a bit distasteful. That is, adding and subtracting numbers in different units. Even though for the computations all are internally turned into consistent units. It still irks my inner engineer.
Is this similar example equally or less irk-provoking?
3 million / 4 thousand - 7 hundred = 50
I'm not sure of my own decision to that question.
Sign in to participate
