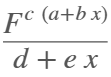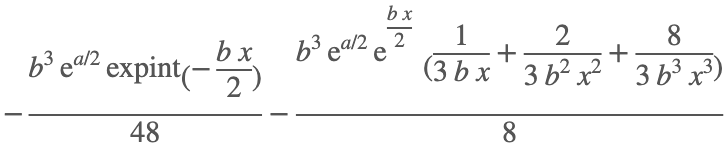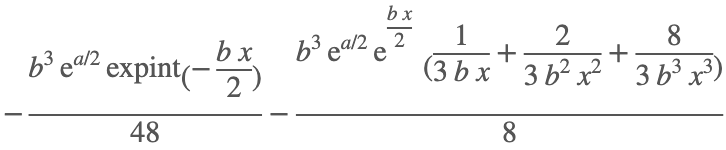I = 
Support for Rubi integration rules
Gregory Vernon
on 3 Oct 2025
Latest activity Reply by Christopher Creutzig
on 8 Oct 2025
Something that I periodically wonder about is whether an integration with the Rubi integration rules package would improve symbolic integration in Matlab's Symbolic Toolbox. The project is open-source with an MIT-licensed, has a Mathematica implementation, and supposedly SymPy is working on an implementation. Much of my intrigue comes from this 2022 report that compared the previous version of Rubi (4.16.1) against various CAS systems, including Matlab 2021a (Mupad):

While not really an official metric for Rubi, this does "feel" similar to my experience computing symbolic integrals in Matlab Symbolic Toolbox vs Maple/Mathematica. What do y'all think?
8 Comments
Time DescendingThanks for this. I have brought it to the attention of the relevant teams internally at MathWorks.
Good idea,the report initially looks very compelling. If it could be integrated with or referenced by the MATLAB Symbolic Toolbox, it would be very valuable for the MATLAB product. I recommend that you directly submit a feature-request via technical support: https://www.mathworks.com/support/contact_us.html
-----
By the way, earlier this year I accidentally came across a Python hyperparameter optimization framework Optuna that is very difficult to use in MATLAB, and I hope this functionality will be enhanced in future versions of MATLAB.
I did a very quick perusal of that 2022 report. Keep in mind that no mupad result could be given an A grade.
I checked the first result in section 3.1 (page 50), which at the time it was claimed that R2021a did not return a result. But it does return the correct result here in 2025b.
matlabRelease
syms F c a b d e m x
I = F^(c*(a+b*x))*(d+e*x)^m
int(I,x)
And here is 3.7, which also was graded as a failure, but now returns the expected result.
I = F^(c*(a+b*x))/(d+e*x)
int(I,x)
It would be interesting to see a comprehensive comparison, perhaps showing the evolution from 2021a to 2025b.
Sign in to participate