1,182 results

Repack of Mi(xed) Da(ta) S(ampling) regressions (MIDAS) written by Eric Ghysels and collaborators

The mixed frequency regression studies the explanatory power of high frequency variables on the low frequency outcome. The weights associated with high frequency regressors are usually assumed some

Bivariate kernel density, kernel regression, and kernel quantile regression

Returns, for two data series:Marginal kernel densitiesBivariate kernel densityConditional kernel densityNadaraya-Watson kernel regressionkernel quantile regressionMethod: Gaussian kernel, Silverman

Quantile regression with bootstrapping confidence intervals

Quantile Regression USAGE: [p,stats]=quantreg(x,y,tau[,order,nboot]); INPUTS: x,y: data that is fitted. (x and y should be columns) Note: that if x is a matrix with several columns

Variational Bayesian Monte Carlo (VBMC) algorithm for Bayesian posterior and model inference in MATLAB

Quantile regression

Quantile regression with LP or interior method.It has kernel test and wald test.See example in readme.m

Learn how to use MATLAB and R together to tackle your computational needs

Non-crossing polynomial quantile regression

ncquantreg finds the coefficients of a polynomial p(x) of degree n that fits the data in vector x to the quantiles tau of y.ncquantreg(x,y) performs median regression (tau = 0.5) using a polynomial

Performs polynomial regression on multidimensional data.

Performs Multivariate Polynomial Regression on multidimensional data. The fits are limited to standard polynomial bases with minor modification options. Feel free to implement a term reduction

Quantile-quantile plot with patch option

NOTE: this function is now available from the IoSR Matlab Toolbox as iosr.statistics.qqPlot. ------------------------- qq_plot(y) displays a quantile-quantile plot of the sample quantiles of y versus

Quantile Probability Plot

This code generates Quantile Probability Plots, often used in investigating the distribution of reaction times when there are several conditions and several subjects. With this code you can easily

Quantiles of a sample via various methods

NOTE: this function is now available from the IoSR Matlab Toolbox as iosr.statistics.quantile. ------------------------- This function calculates quantiles and weighted quantiles for vectors

computes the normal quantile function with high precision for extreme values in the tail

computes the quantile function of the standard normal distribution, truncated to the interval [l,u].Method designed for precision in the tails. Inf values for vectors 'l' and 'u' accepted;%Example

Graphical and numerical functions for data analysis

Application of ANFIS to multi-variable nonlinear regression, function approximation and modleing

For more information, see following links:http://yarpiz.com/301/ypfz101-nonlinear-regression-using-anfis

Fit data points with a five points logistic regression or interpolate data.

Five parameters logistic regressionOne big holes into MatLab cftool function is the absence of Logistic Functions. In particular, The Five Parameters Logistic Regression or 5PL nonlinear regression

Fit data using orthogonal linear regression.

each datapoint DATA(i,:) -- LINORTFITN finds N and C such that the sum of squared distances is minimized.There is already a file in Matlab Central for orthogonal linear regression in 2 dimensions, but it

A Matlab toolbox for sampling inverse problems with complex prior information.

Stacked line plots from a matrix or vectors

Return sound pressure levels of pure tone frequencies at specified loudness level(s).

Calculate RT, DRR, Cte, and EDT for impulse response file

Apply a near-ideal low- or band-pass filter.

Produce an array of responses from a fourth-order Gammatone filter via FFT

Fit data points with a four points logistic regression or interpolate data.

Four parameters logistic regression.One big holes into MatLab cftool function is the absence of Logistic Functions. In particular, The Four Parameters Logistic Regression or 4PL nonlinear regression

A non-parametrical regression (smoothing) tool using Gaussian kernel.

Non-parametric regression is widely used in many scientific and engineering areas, such as image processing and pattern recognition.Non-parametric regression is about to estimate the conditional

Draw a box plot with various display options

Automated construction of a legend. - Set box limits as percentiles. - Set whisker extent via various methods.- Use of weighted quantiles.- Creation of violin plots.

The STK is a (not so) Small Toolbox for Kriging

Experiments(DACE), the STK can be useful for other applicationsareas (such as Geostatistics, Machine Learning,Non-parametric Regression, etc.).Copyright: Large portions are Copyright (C) 2011-2014 SUPELECand

Linear regression using: Direct Method, Inbuilt function, SGD Method

Linear regression attempts to model the relationship between two variables by fitting a linear equation to observed data. One variable is considered to be an explanatory variable, and the other is

Improved quantile inference for one- and two-sample (e.g., treatment vs. control) cases

Detailed documentation includes further explanation and examples; just type "help quantile_inf". The following briefly describes functionality as well as the theoretical foundations from the

Estimates a Student's t regression model

Estimates a Student's t regression model:y = X*beta + epswhere eps ~ Student's t (0, sigma, nu).with nu > 2.Parameters are estimated with maximum likelihood.

Draw the so called Murphy Diagram to compare point forecasts

the following paper:Ehm, W., Gneiting, T., Jordan, A. and Krueger, F. (2016), Of quantiles and expectiles: consistent scoring functions, Choquet representations and forecast rankings. J. R. Stat. Soc. B

Efficient nonlinear regression fitting using a constrained, partitioned least squares overlay to fmi

I need to thank Duane Hanselman for suggesting this great idea.Fminspleas is a simple nonlinear least squares tool that fits regression models of the formY = a1*f1(X,C) + a2*f2(X,C) + ... +

Sample code to plot linear regression curve with confidence intervals.

This is a simplified code to generate a linear regression curve for your paper/report/assignment. Just replace the sample data and comment the line 17 : axis([0.04 0.3 0.03 .35]);This code is

A variety of regression utilities

This zip file contains 11 functions related to regression. The functions are:1) cookdist.m - Cook's distance for data points2) dregr.m - Deming regression3) irsvdregr.m - Iterative Reweighted Least

Ogive optimization toolbox for deriving surface fluxes in challenging environments

Low-Rank and Sparse Tools for Background Modeling and Subtraction in Videos

Optimization using the evolutionary algorithm of Differential Evolution.

Boosted Binary Regression Trees is a powerful regression method which can handle vector targets.

Boosted Binary Regression Trees (BBRT) is a powerful regression method proposed in [1]. BBRT combines binary regression trees [3] using a gradient boosting technique.There are several variants

deming perfoms a linear Deming regression. Useful when errors are present in both x and y variables.

[ b sigma2_x x_est y_est stats] = deming(x,y,lambda,alpha)deming() performs a linear Deming regression to find the linear coefficients: y = b(1) + b(2)*xunder the assumptions

Water electrolysis modelling toolbox for UI curve parametrization

Calculates slope and intercept for linear regression of data with errors in X and Y.

Calculates slope and intercept for linear regression of data with errors in X and Y. The errors can be specified as varying point to point, as can the correlation of the errors in X and Y.The

Calculate the long-term average spectrum of a signal

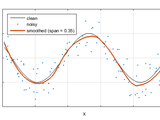
LOESS performs a locally weighted regression fit to noisy data

Function fLOESS performs LOESS (locally weighted non-parametric regression fitting using a 2nd order polynomial) smoothing to one dimensional data, without the Matlab Curve Fitting Toolbox. This

Some tools for geostatistical analysis

Geometric Mean Regression (Reduced Major Axis Regression).

Model II regression should be used when the two variables in the regression equation are random and subject to error, i.e. not controlled by the researcher. Model I regression using ordinary least

MNI2FS: High Resolution Surface Rendering of MNI Space Volumes

Gaussian Process Regression using GPML toolbox V4.2

MatDRAM is a pure-MATLAB Adaptive Markov Chain Monte Carlo simulation and visualization library.

, sampling, and integration of mathematical objective functions of arbitrary-dimensions, in particular, the posterior probability distributions of Bayesian regression models in data science, Machine Learning

Highly comparative time-series analysis

plot quantiles of y given quantiles of x.

inter-quartile range. X and Y must have the same number of rows or columns.This is useful to visualize two-dimensional distributions.Options include e.g.: plotting different quantiles; means/variances instead of

Produces a colour colormap, of arbitrary length, that is monochrome-compatible.

Calculate subplot positions by specifying figure margins and axis scaling.

Removes outliers from X and Y variables based on regression residuals

This function accepts two (vector of) variables for which a bivariate linear regression analysis is meant to be performed, and removes the outliers from both variables. Since the regression residual

Encoding of data in Gaussian Mixture Model and retrieval through Gaussian Mixture Regression

GMM-GMR is a set of Matlab functions to train a Gaussian Mixture Model (GMM) and retrieve generalized data through Gaussian Mixture Regression (GMR). It allows to encode efficiently any dataset in

A function to provide local linear estimator of Gaussian kernel regression

This is the local linear version of the kernel smoothing regression function: http://www.mathworks.com/matlabcentral/fileexchange/loadFile.do?objectId=19195&objectType=FILEThe local linear

Perform windowed smoothing on a vector using mathematical functions

Curve fitting, empirical modeling, and an appreciation of shape

The art of fitting a nonlinear regression model often starts with choosing a model form. This submission is an attempt to teach the reader a simple but general paradigm for their models as a sum of

Passing & Bablok regression is a linear regression procedure usefull for comparing clinical methods

. Classical linear regression method assume that variables X and Y are normal distributed and with a measurement error costant over the range of concentrations.However, in method comparison studies we generally

This is ridge regression implemented using the Gaussian Kernel.

The Gaussian Kernel can be changed to any desired kernel. However such a change will not dramatically improve results. This is a variant of ridge regression using the kernel trick (Mercers Theorem).

This is a set of MATLAB functions to do Bayesian linear regression

This is a set of MATLAB functions to do Bayesian linear regression. Derivations are also included.

Perform regression on plotted data in a figure by manually choosing the regression area.

Plot data in a figure, and then interactively choose regression area. The result from polyfit is returned.Example:x=1:1:10;y=sin(x);f=figure; plot( x,y );[p,h] = figreg( f, 2 );%fit a second order