comm.PhaseNoise
Apply phase noise to baseband signal
Description
The comm.PhaseNoise
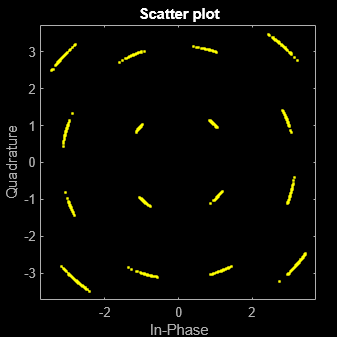
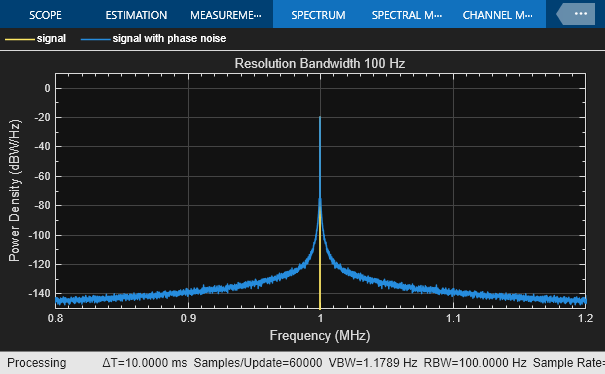
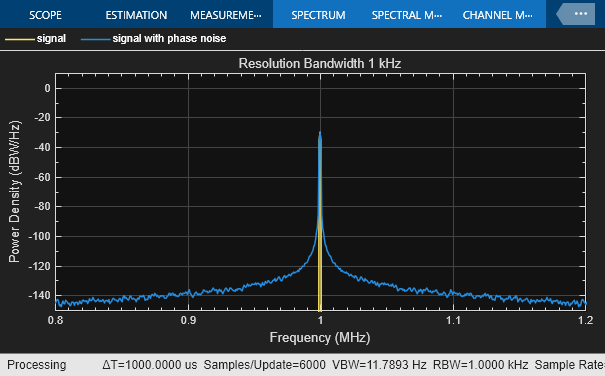
System object™ adds phase noise to a complex signal. This object emulates impairments
introduced by the local oscillator of a wireless communication transmitter or receiver. The
object generates filtered phase noise according to the specified spectral mask and adds it to
the input signal. For a description of the phase noise modeling, see Algorithms.
To add phase noise using a comm.PhaseNoise object:
Create the
comm.PhaseNoiseobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
phznoise = comm.PhaseNoise
phznoise = comm.PhaseNoise(level,offset,samplerate)
phznoise = comm.PhaseNoise(___,Name=Value)comm.PhaseNoise(RandomStream="mt19937ar with seed"), creates a phase
noise object with the random stream set to use the Mersenne Twister random number
generator.
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
References
[1] Kasdin, N. J. "Discrete Simulation of Colored Noise and Stochastic Processes and 1/(f^alpha); Power Law Noise Generation." The Proceedings of the IEEE® 83, no. 5 (May, 1995): 802–27.